JAMB Mathematics Previous Year Questions: 2022 | Mathematics for JAMB PDF Download

Q1: Solve for k in the equation 1/8^k+2 = 1
(a) 2
(b) -4
(c) -2
(d) 4
Ans: (c)
(8^-1)^k+2 = (8⁰)
cancel out base 8:
-1(k+2) = 0
-k -2 = 0
k = -2

Q2: Evaluate (101 _two)³
(a) 111101_two
(b) 11111101_two
(c) 1111101_two
(d) 11001_two
Ans: (c)
(101_two)³ = (5_ten)³
5³ = 125
And 125 =  1111101_two 

Q3: The shaded portion in the Venn diagram below represents...?
(a) F - (E n F) - (G n F)
(b) E' n F n G'
(c) E u F u G
(d) F
Ans: (b)

• we can express the diagram as E' n F n G'
• sets E and G are present in the Universal Set but are not included in the expression
• the shaded portion in the diagram is set F

Q4: If a fair coin is tossed twice, what is the probability of obtaining at least one head?
(a) 0.25
(b) 0.75
(c) 0.5
(d) 0.33
Ans: (b)
S=HH, HT, TH, TT
We can get the result by subtracting the probability of getting no heads with 1.
That is, the probability of getting at least one head = 1 minus the probability of getting no heads:
P=1?1/4
= 3/4
= 0.75

Q5: Give that the mean of 2, 5, (x+1), (x+2), 7 and 9 is 6, find the median.
(a) 5.5
(b) 5
(c) 6.5
(d) 6
Ans: (c)
To find the value of x,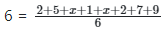

6 * 6 = 2 + 5 + x+1 + x+2 + 7 + 9
36 = 2x + 26
36 - 26 = 2x
10 = 2x
x = 5
median = 7+6/2
= 6.5

Q6: If sin ?  and θ lies in the third quadrant, find cos θ
(a) 4/5
(b)
(c) 5/4
(d)
Ans: (d)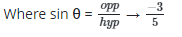

opp = -3, hyp = 5
using Pythagoras' formula:
hyp² = adj² + opp²
adj² = hyp² - opp²
adj² = 5² - 3² → 25 - 9
adj² = 16
adj = 4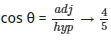

In the third quadrant, cos θ is negative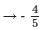

Q7:  Simplify 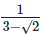 in the form of p + q√2
(a)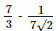
(b)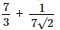
(c)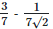
(d)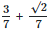
Ans: (d)
Rationalization with conjugate 3+√2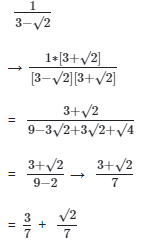


Q8: Find the length of a chord 3cm from the centre of a circle of radius 5cm.
(a) 8cm
(b) 5.6cm
(c) 7cm
(d) 6.5cm
Ans: (a)
Using the Pythagoras theorem,
Hyp² = adj² + opp²
5² = opp² + 3²
5² - 3² = adj²
4 = adj
Hence, length of the chord = 2 * 4 = 8cm

Q9: Mr Adu spends his annual salary on food(f), rent(r), car maintenance, gifts(g), savings(s) and some miscellaneous (m) as indicate in the table below: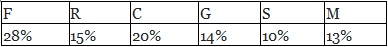
(a) 108.5
(b) 100.8
(c) 98.8
(d) 120.5
Ans: (b)

= 10.8º

Q10: A rectangular pyramid has an area of 24cm² and a height of 7.5cm. Calculate the volume of the pyramid.
(a) 65.0cm³
(b) 70.5cm³
(c) 56.5cm³
(d) 60.0cm³
Ans: (d)
Volume of a rectangular pyramid,


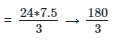
Volume of the rectangular pyramid = 60cm³

Q11: The 10th term of an AP is 32. If the first term is 3/2, what is the 4th term?
(a) 35/3
(b) 64
(c) 16
(d) 35/2
Ans: (a)
Tn = a + (n-1)d
10th term = 32
32 = 3/2 + 9d
9d = 32 - 3/2
9d = 61/2
d = 61/18
T4 = 3/2 + 3(61/18)
T4 = 3/2 + 61/6 → 35/3

Q12: Tanθ is positive and Sinθ is negative. In which quadrant does ? lies
(a) Third only
(b) Fourth only
(c) First and third only
(d) Second only
Ans: (a)
In the third quadrant where the tangent of any angle is positive.
The sine and cosine of any angle between 180 and 270 degrees are negative.

Q13: In how many ways can the letter of ZOOLOGY be arranged?
(a) 720
(b) 360
(c) 840
(d) 120
Ans: (c)
Zoology has 7 letters in total, with O repeated thrice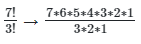

= 840ways

Q14: Integrate (2x+1)³
(a)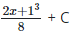
(b)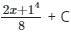
(c)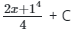
(d)
Ans: (b)
Recall chain rule: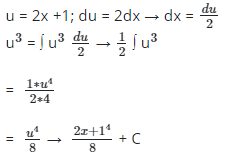


Q15: If  and  Find AB
(a)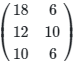
(b)
(c)
(d)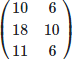
Ans: (d)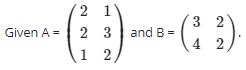

We can multiply these matrices since the number of colums in A = number of rows in B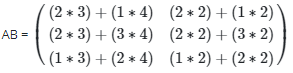




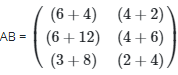
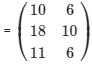
Q16: Given that 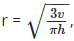 make v the subject of the formula
(a) v = 3 πr²h
(b) v = πrh/3
(c) v = πr²h/3
(d) v = 3πrh
Ans: (c)
square both sides to remove the big square root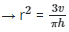

cross multiply
3v = r² * πh
v = πr²h/3

Q17: Find the determinant of the matrix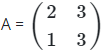
(a) 4
(b) 2
(c) 5
(d) 3
Ans: (d)
|A| = (2*3) - (1*3)
→ 6 - 3
= 3

Q18: Evaluate Log₂ 8√2
(a) 3.0
(b) 4.5
(c) 3.5
(d) 2.5
Ans: (c)
where Log₂ 8√2 → Log₂ √128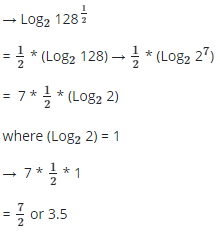


Q19: The locus of points equidistant from a fixed point.
(a) circle
(b) perpendicular lines
(c) straight line
(d) bisector
Ans: (a)
The locus of points equidistant from a fixed point forms a circle. A circle is defined as the set of all points in a plane that are equidistant from a fixed point, known as the center of the circle. The distance from any point on the circle to the center remains constant, resulting in the characteristic shape of a circle.

Q20: What will be the result obtained when the numerator of 96/50 is decreased by 37.5% and its denominator decreased by 20%.
(a) 1.5
(b) 5/2
(c) 96/48
(d) 0.5
Ans: (a)
Numerator: 96 → 37.5% of 96 = 36
Decreased by 36 → 96 - 36
New numerator = 60
Denominator: 50 → 20% of 50 = 10
Decreased by 10 → 50 - 10 = 40
New Denominator = 40
New fraction = 60/40 or 1.5

Q21: A poultry farmer realized 200 eggs from his birds and sold 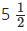 crates of eggs. What percentages of eggs are left?
(a) 82.5%
(b) 15%
(c) 17.5%
(d) 85%
Ans: (c)
5 crates = 30 eggs * 5 = 150eggs
1/2 crate = 15 eggs
Total sold = 165
remainder = 200 - 165 = 35
And 35 is equivalent 17.5% of the realized eggs

Q22: If sec²θ + tan²θ = 3, then the angle θ is equal to?
(a) 90º
(b) 30º
(c) 45º
(d) 60º
Ans: (c)
Given that sec² θ + tan² θ = 3
Where sec² θ = 1  + tan² θ :
1 + tan² θ + tan² θ = 3
2tan² θ = 3 - 1
2tan² θ = 2
divide both sides by 2
tan² θ = 1
tanθ =  √1
tanθ = 1
θ = tan−1 (1)
θ = 45º

Q23: Find the limit of 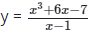 as x tends to 1
(a) 9
(b) 8
(c) 0
(d) 7
Ans: (a)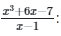

When numerator is differentiated → 3x²+ 6  
When denominator is differentiated → 1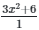

substitute x for 1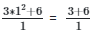

= 9/1
= 9

Q24: Find the equation of a straight line parallel to the line 2x - y = 5 and having intercept of 5
(a) 2x + y = 5
(b) 2x + y = -5
(c) 2x - y = -5
(d) 2x - y = 5
Ans: (c)
Condition for Parallelism means that their gradient value is same
line 2x - y = 5 is rearranged
As y = 2x - 5 from y = mx + c
line 2x - y = 5 has the gradient of 2
A parallel line with gradient of 2 and intercept of 5
→ 2x - y = -5
Rearranged as y = 2x + 5

Q25: Calculate the median of 14, 17, 10, 13, 18 and 10.
(a) 12.5
(b) 13.5
(c) 13.2
(d) 14.5
Ans: (b)
When rearranged: 10, 10, 13, 14, 17, 18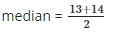

= 27/2 or 13.5

Q26: The equivalent of (10110.011)₂ in base 10 is?
(a) 26.325
(b) 24.372
(c) 42.443
(d) 22.375
Ans: (d)
Using the expansion method on (10110.011)₂ 
(1 * 2⁴) + (0 * 2³) + (1 * 2²) + (1 * 2¹) (0 * 2⁰) + (0 * 2⁻¹) + (1 * 2⁻²)  + (1 * 2⁻³)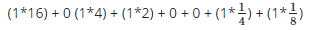

16 + 4 + 2 + (0.25 + 0.125)
22 + 0.375
(10110.011)₂ = 22.375₁₀

Q27: The cost C of running a school is directly proportional to the number of students N, if 20 students cost #10,000, How many students can #1,000,000 cover?
(a) 3000
(b) 1000
(c) 2000
(d) 4000
Ans: (c)
if 20 students = 10000
#500 per student
#1,000,000 ÷ 500
= 2,000 cover students

Q28: The coordinates of the mid-point of the line joining the points (-3,5) and (2,10) is given by?
(a) (1/2 , 15/2)
(b) (1/2 , -15/2)
(c) (-1/2 , -15/2)
(d) (-1/2 , 15/2)
Ans: (d)
Given Data: x₁ = -3,  x₂ = 2,  y₁ = 5,  y₂ = 10
coordinates of the mid-point of the line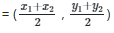


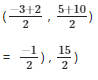
Q29: Evaluate 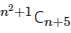 if n = 3
(a) 55
(b) 45
(c) 35
(d) 25
Ans: (b)

= 45

Q30: Given that S = 3t² + 5t - 10 is displacement of a particle in metres, calculate it initial velocity.
(a) 10m/s
(b) 2m/s
(c) 5m/s
(d) 6m/s
Ans: (c)
To find the initial velocity, we need to differentiate the displacement equation with respect to time. Taking the derivative of S(t) will give us the velocity function.
Given:
S(t) = 3t² + 5t - 10
Differentiating S(t) with respect to t:
V(t) = dS(t)/dt = d/dt (3t² + 5t - 10)
V(t) = 6t + 5
The initial velocity is the value of V(t) at t = 0, which gives us:
V(0) = 6(0) + 5 = 5 m/s
Therefore, the initial velocity is 5 m/s, and the correct answer is (c).

Q31: In the diagram below, XY = 8cm and OX = 5cm. Find Oz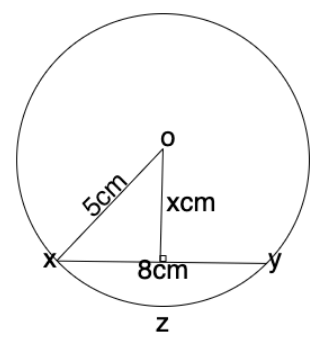
(a) 9cm
(b) 3.4cm
(c) 9.1cm
(d) 3cm
Ans: (d)
hyp = 5cm, adj = 8cm/2 = 4cm, opp = xcm
Pythagoras theorem:
hyp² = opp² + adj² 
5² = x² + 4² 
x² = 25 - 16
x = √9
x = 3cm

Q32: Let (*) be a binary operation on a natural number defined by a * b = a - b + (ab)², then find 3 * 5
(a) 223
(b) 232
(c) 32
(d) -232
Ans: (a)
3 * 5 = 3 - 5 + (3 x 5)²
-2 + (15)²
-2 + 225
= 223

Q33: If y varies inversely as x and x = 3 when y =4. Find the value of x when y = 12
(a) 4
(b) 1
(c) 2
(d) 3
Ans: (b)
y = 1/x; y = k/x
k = xy → 3 * 4 = 12
3 * 4 = 12
x = k/y
x = 12/12 = 1

Q34: If 8, p, q and 26 is an A.P. Find the values of p and q
(a) p = 14 and q = 14
(b) p = 20 and q = 14
(c) p = 20 and q = 20
(d) p = 14 and q = 20
Ans: (d)
The common difference is 6.
Just add 6 to get the next term
8, 14, 20 and 26

Q35: Find x if the mean of 2x, 4x, 2x - 13 and 6x is 4.
(a) 1.5
(b) 2.0
(c) 1.0
(d) 0.5
Ans: (b)
mean (4)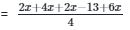
16 = 14x - 13
16 + 13 = 14x
x = 29/14 or 2.07

Q36: Factorize 4a² - 9b² 
(a) (2a-3b) (2a+3b)
(b) (2a-b) (2a+3b)
(c) (2a-3b) (a+3b)
(d) (a-3b) (a+3b)
Ans: (a)
(2a-3b) (2a+3b)
4a² + 6ab - 6ab - 9b² 
4a² - 9b² 

Q37: If n(P) = 20 and n(Q) = 30 and n(PuQ) = 40, find the value n(PnQ)
(a) 10
(b) 30
(c) 15
(d) 40
Ans: (a)
n(PuQ) = n(p) + n(q) -  n(PnQ)
40 = 20 + 30 -  n(PnQ)
n(PnQ) = 50 - 40 = 10

Q38: Three times a certain number (x), minus 2 is less than the number minus 6.Find the possible values of x.
(a) x <-2
(b) x>2
(c) x>-2
(d) x<2
Ans: (a)
Three times a certain number (x) = 3x
minus 2 = -2
is less than = <
the number minus 6 = x -6
Mathematically; 3x - 2 < x - 6
collect like terms
3x - x < -6 + 2
2x < -4
x < -2 is  the possible values of x

Q39: The number line is represented by inequality.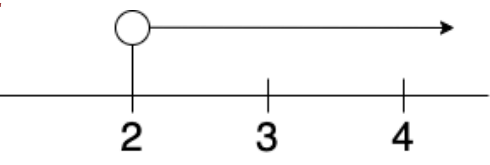
(a) x ≤ 2
(b) x < 2
(c) x ≥ 2
(d) x > 2
Ans: (c)
x ≥ 2 is represented by an arrow with an filled-in dot above the 2.
The arrow points in the direction of all the numbers that are greater than 2.

Q40: If a dress is sold for #3800.00 at 20% discount. what is its original price?
(a) #3,000.00
(b) #4,000.00
(c) #5,000.00
(d) #4,750.00
Ans: (d)
It is given that the cost of the item reduces to #3800.00 after the discount on the item.
Let original price = x
x – (20% of x) = 100
⇒ x – 0.2x = 100
⇒ 0.8x = #3800
⇒ x = 3800/0.8
⇒ x = 4,750