JEE Advanced (Fill in the Blanks): Differentiation | Chapter-wise Tests for JEE Main & Advanced PDF Download
Fill in the Blanks
Q. 1. 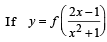 and f '(x) = sin x2 , then
and f '(x) = sin x2 , then 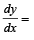 ....................
....................
Ans. 
Solution.
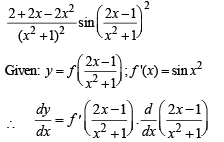

Q. 2. If fr (x), g (x), hr (x) r , r = 1, 2, 3 are polynomials in x such that fr(a) = gr (a) = hr(a), r = 1, 2, 3
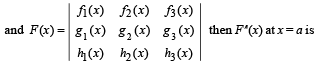
....................
Ans. 0
Solution.
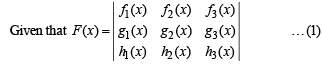
Where fr(x), gr(x), hr(x), r = 1, 2, 3, are polynominals in x and hence differentiable and
fr(a) = gr(a) = hr(a), r = 1, 2, 3 … (2)
Differentiating eq. (1) with respect to x, we get
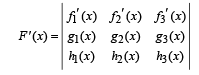
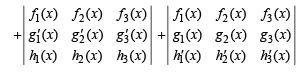
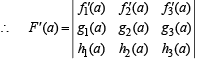
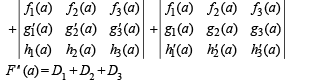
Using eq. (2) we get D1 = D2 = D3 = 0 [By the property of determinants that D = 0 if two rows in D are identical]
∴ F' (a) = 0.
Q. 3. If f(x) = logx (ln x), then f '(x) at x = e is ....................
Ans. 1/e
Solution. Given that
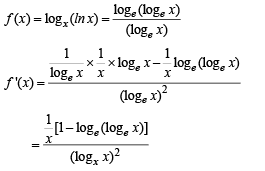
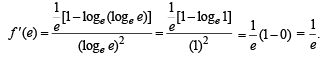
Q. 4. The derivative of 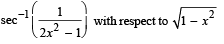 at = 1/2 is .......
at = 1/2 is .......
Ans. 4
Solution.
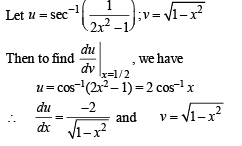
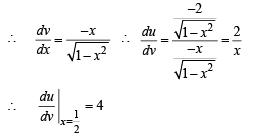
Q. 5. If f (x) = | x – 2 | and g(x) = f [f(x)], then g'(x) = .................... for x > 20
Ans. 1
Solution. f (x) = | x – 2 |
⇒ g (x) = f (f (x)) = | f (x) – 2 | as x > 20
= || x - 2| -2 | = |x - 2- 2| as x > 20 = | x – 4 |
= x – 4 as x > 20
∴ g' (x) = 1
Q. 6. If xexy = y + sin2 x, then at x = 0, dy/dx = ......
Ans. 1
Solution. Given : xexy = y + sin2 x
Differentiating both sides w. r.to x, we get
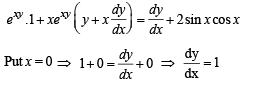
True/ False
Q. 1. The derivative of an even function is always an odd function.
Ans. T
Solution. 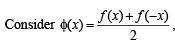 , which is an even function
, which is an even function
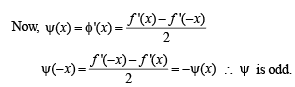
|
446 docs|929 tests
|
















