JEE Main Previous Year Questions (2016- 2024): Definite Integrals and Applications of Integrals | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. The area of the region, enclosed by the circle x2 + y2 = 2 which is not common to the region bounded by the parabola y2 = x and the straight line y = x, is (2020)
(1) 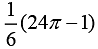
(2) 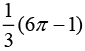
(3) 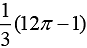
(4) 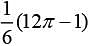
Ans. (4)
The given equation of circle is
x2 + y2 = 2.... (1)
Now, total area enclosed by the circle is πr2 = π(√2)2 = 2π sq. units
The area bounded by the parabola y2 = x and y = x is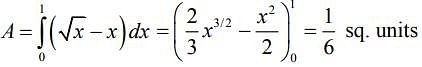
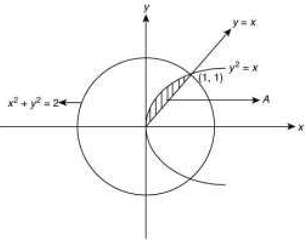
Hence, the required area of the region = 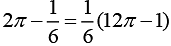 sq. units
sq. units
Q.2. The area (in sq. units) of the region 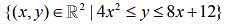 is (2020)
is (2020)
(1) 125/3
(2) 128/3
(3) 124/3
(4) 127/3
Ans. (2)
The given curves are 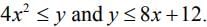
Now, on solving y = 4x2 and y = 8x + 12, we get
4x2 - 8x - 12 = 0 ⇒ x2 - 2x - 3 = 0
x = -1, 3 and y = 4, 36
Therefore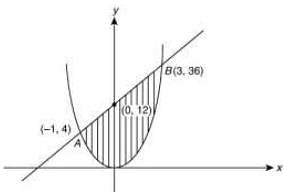
Hence, the area of shaded region is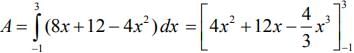
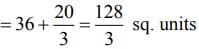
Q.3. For a > 0, let the curves C1 : y2 = ax and C2 : x2 = ay intersect at origin O and at Point P. Let the line x = b (0 < b < a) intersect the chord OP and the x axis at points Q and R respectively. If the line x = b bisects the area bounded by the curves, C1 and C2, and the area of 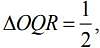 then ‘a’ satisfies the equation: (2020)
then ‘a’ satisfies the equation: (2020)
(1) x6 - 6x3 + 4 = 0
(2) x6 - 12x3 + 4 = 0
(3) x6 + 6x3 - 4 = 0
(4) x6 - 12x3 - 4 = 0
Ans.(2)
We have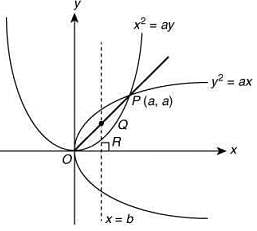
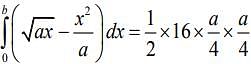
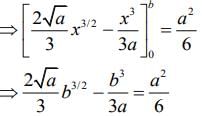 (1)
(1)
Now, the area of triangle PQR = 1/2
Substituting the value of b in Eq. (1), we get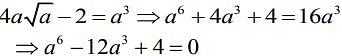
Q.4. The equations of given curves are 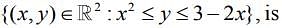 (2020)
(2020)
(1) 32/3
(2) 34/3
(3) 29/3
(4) 31/3
Ans. (1)
The equations of given curves are
x2 < y... (1)
2x + y < 3... (2)
On solving y = x2 = and 2x + y = 3, we get the intersection point x = − 1, 3.
Now,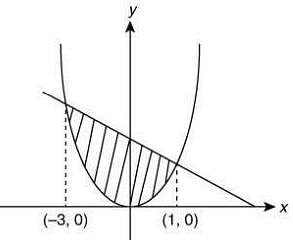
Hence, the area of shaded region is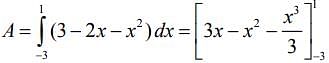
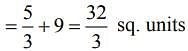
Q.5. Given: 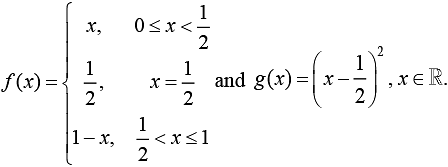 Then, the area (in sq. units) of the region bounded by the curves, y = f(x) and y = g(x) between the lines 2x = 1 and 2x =√3 is (2020)
Then, the area (in sq. units) of the region bounded by the curves, y = f(x) and y = g(x) between the lines 2x = 1 and 2x =√3 is (2020)
(1) 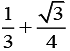
(2) 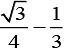
(3) 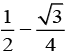
(4) 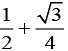
Ans. (2)
We have,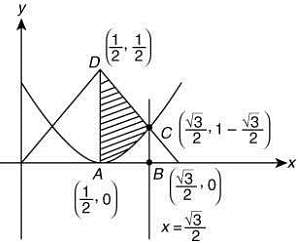
Required area, A = Area of trapezium ABCD 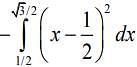
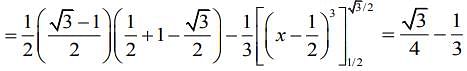 sq. units
sq. units
Q.6. The value of α for which 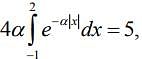 is (2020)
is (2020)
(1) loge2
(2)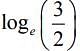
(3)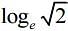
(4) 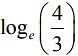
Ans. (1)
We have,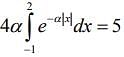

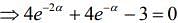

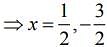
Thus, 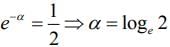
Q.7. If 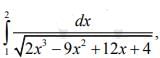 then (2020)
then (2020)
(1)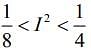
(2)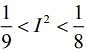
(3)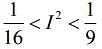
(4)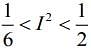
Ans. (2)
We have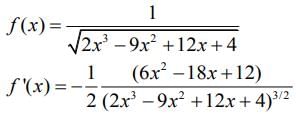
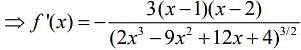
Therefore, f (x) is decreasing in (1,2).
Now,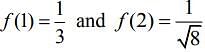
Hence, 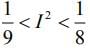
Q.8. If for all real triplets (a, b, c), f(x) = a + bx + cx2 ; then 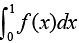 is equal to (2020)
is equal to (2020)
(1) 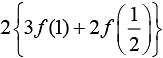
(2) 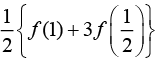
(3) 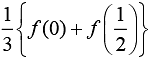
(4) 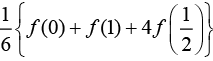
Ans. (4)
We have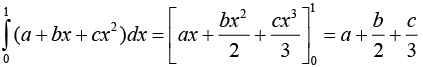 .... (1)
.... (1)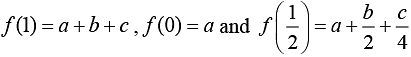
Now, 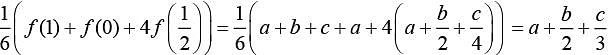
Q.9. Let z be a complex number such that 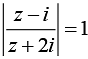 and
and 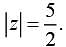 Then, the value of
Then, the value of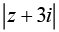 is (2020)
is (2020)
(1) √10
(2) 7/2
(3) 15/4
(4) 2√3
Ans. (2)
We have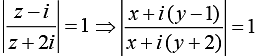
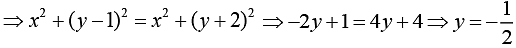
and 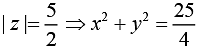
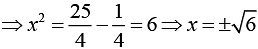
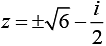
Now, 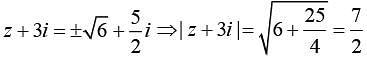
Q.10. If f(a + b + 1 - x) = f(x), for all x, where a and b are fixed positive real numbers, then 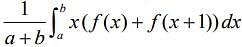 is equal to (2020)
is equal to (2020)
(1) 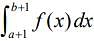
(2) 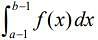
(3) 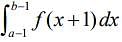
(4) 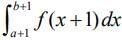
Ans.
Given,
f(x) = f(a + b + 1 - x)...(1)
f(x + 1) = f (a + b - x)...(2)
Now,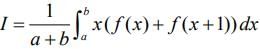 ....(3)
....(3)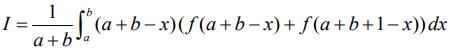
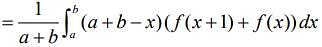 ....(4)
....(4)
From Eqs. (2) and (3), we get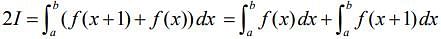
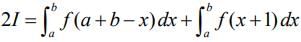
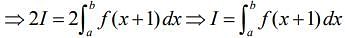
Let x + 1 = t ⇒ dx = dt, so 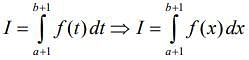
Q.11. The value of 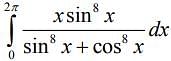 is equal to (2020)
is equal to (2020)
(1) 2π
(2) 2π2
(3) π2
(4) 4π
Ans. (3)
We have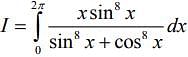 .... (1)
.... (1)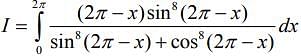
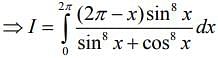 (2)
(2)
From Eqs. (1) and (2), we get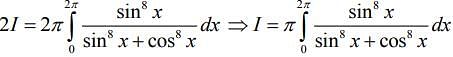
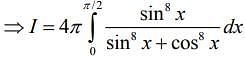 .... (3)
.... (3)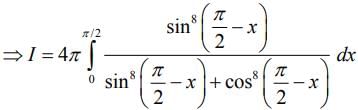
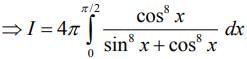 (4)
(4)
From Eqs. (3) and (4), we get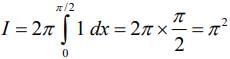
Q.12. If 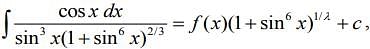 where c is a constant of integration, then
where c is a constant of integration, then 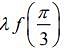 is equal to (2020)
is equal to (2020)
(1) 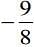
(2) 2
(3) 9/8
(4) -2
Ans. (4)
Given,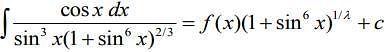 ... (1)
... (1)
Now,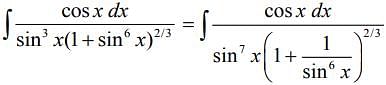
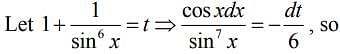
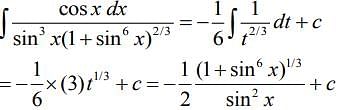 ...(2)
...(2)
From Eqs. (1) and (2), we get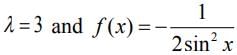
Hence,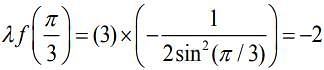
Q.13. 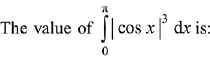 (2019)
(2019)
(1) 0
(2) 4/3
(3) 2/3
(4) -4/3
Ans. (2)
Solution.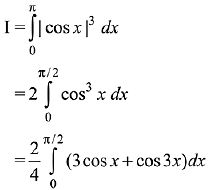
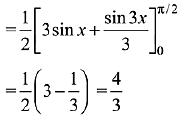
Q.14. Let f be a differentiable function from R to R such that |f(x) - f(y)|≤ 2|x - y|3/2, for all x, y, ∈ R. If f(0) = 1 then 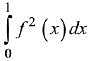 is equal to: (2019)
is equal to: (2019)
(1) 1
(2) 2
(3) 1/2
(4) 0
Ans. (1)
Solution.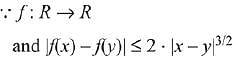
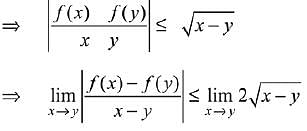
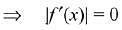
∴ f(x) is a constant function.
Given f(0) = 1 ⇒ f(x) = 1
Hence, the integral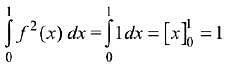
Q.15. 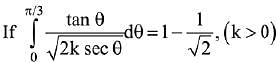 then the value of k is: (2019)
then the value of k is: (2019)
(1) 4
(2) 1/2
(3) 1
(4) 2
Ans. (4)
Solution.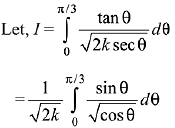
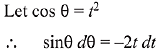
Hence, integral becomes.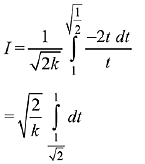
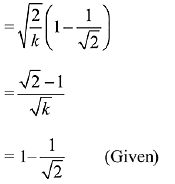
∴ k = 2
Q.16. then f'(1/2) is: (2019)
then f'(1/2) is: (2019)
(1) 24/25
(2) 18/25
(3) 4/5
(4) 6/25
Ans. (1)
Solution.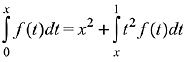
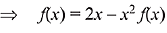
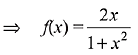
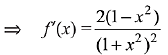
Then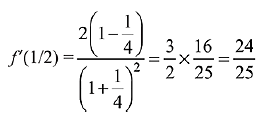
Q.17. Given:  and g (x) =
and g (x) = 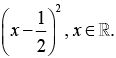 Then, the area (in sq. units) of the region bounded by the curves, y = f (x) and y = g (x) between the lines 2x = 1 and 2x = √3 is
Then, the area (in sq. units) of the region bounded by the curves, y = f (x) and y = g (x) between the lines 2x = 1 and 2x = √3 is
(1)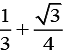
(2)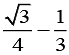
(3)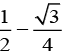
(4)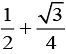
Ans. (2)
We have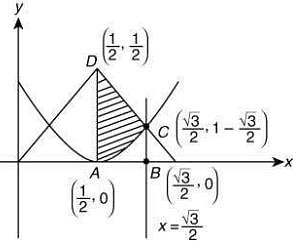
Required area, A = Area of trapezium ABCD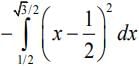
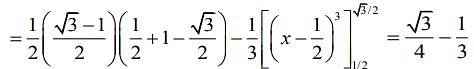 sq. units
sq. units
Q.18. The value of 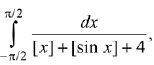 where [t] denotes the greatest integer less than or equal to t, is: (2019)
where [t] denotes the greatest integer less than or equal to t, is: (2019)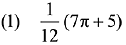
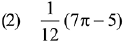
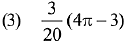
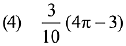
Ans. (3)
Solution.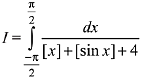
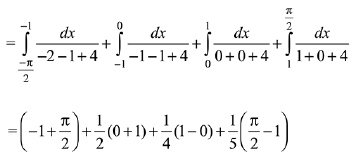
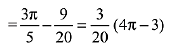
Q.19. The value of the integral 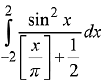
(where [x] denotes the greatest integer less than or equal to x) is: (2019)
(1) 0
(2) sin 4
(3) 4
(4) 4 -sin 4
Ans. (1)
Solution.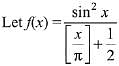
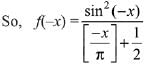
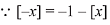
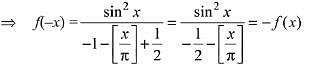
⇒ f(x) is odd function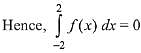
Q.20.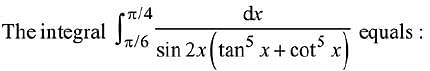 (2019)
(2019)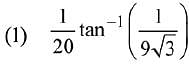
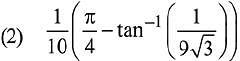
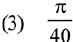
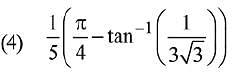
Ans. (2)
Solution.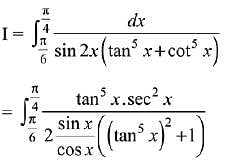
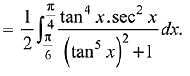
Let tan5x = t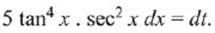
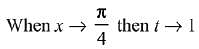
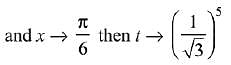
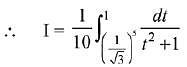
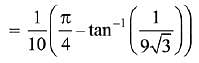
Q.21. Let f and g be continuous functions on [0, a] such that f(x) =f(a - x) and g(x) + g(a - x) = 4, 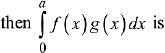 equal to: (2019)
equal to: (2019)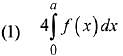
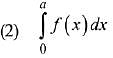
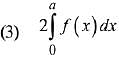
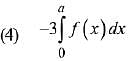
Ans. (3)
Solution.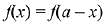
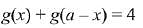
Let, the integral,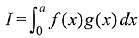
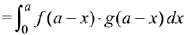
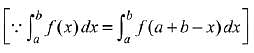
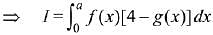
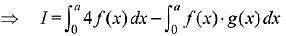
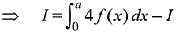
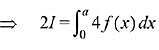
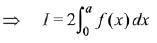
Q.22. The integral 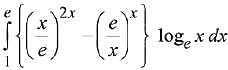 is equal to: (2019)
is equal to: (2019)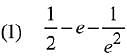
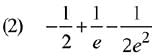
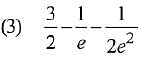
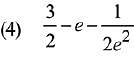
Ans. (4)
Solution.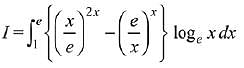
Let 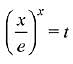
⇒ 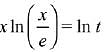
⇒ x (ln x - 1) = ln t
On differentiating both sides w.r.t x we get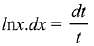
When x = e then t = 1 and when x = 1 then t = 1/e.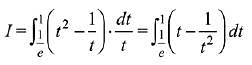
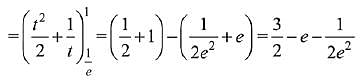
Q.23.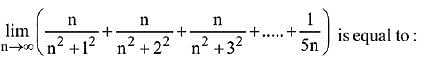 (2019)
(2019)
(1) π/4
(2) tan-1(3)
(3) π/2
(4) tan-1(2)
Ans. (4)
Solution.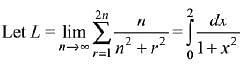
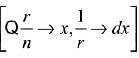
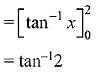
Q.24.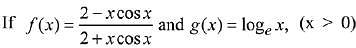 then the value of the
then the value of the
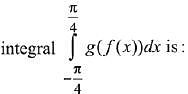 (2019)
(2019)
(1) loge3
(2) logee
(3) loge2
(4) loge1
Ans. (4)
Solution.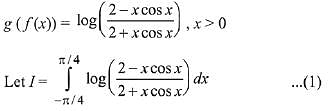
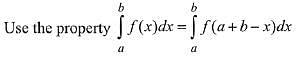
Then, equation (1) becomes,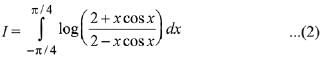
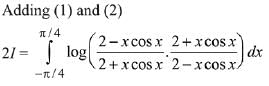
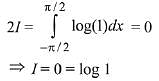
Q.24. 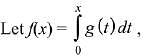 , where g is a non-zero even function. If
, where g is a non-zero even function. If
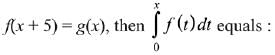 (2019)
(2019)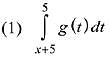
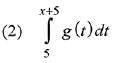
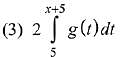
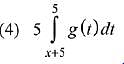
Ans. (1)
Solution.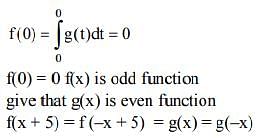
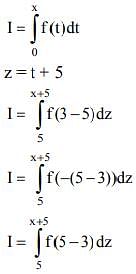
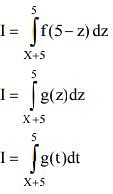
Q.25. 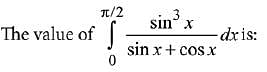 (2019)
(2019)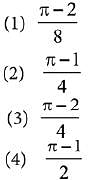
Ans. (2)
Solution.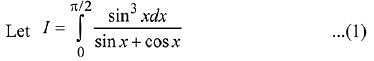
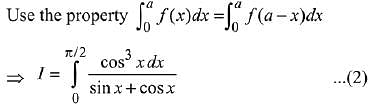
Adding equation (1) and (2), we get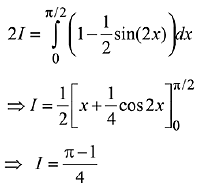
Q.26. The value of the integral 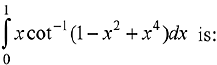 x ∈ [0,1] (2019)
x ∈ [0,1] (2019)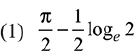
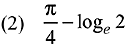
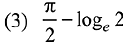
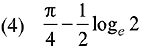
Ans. (4)
Solution.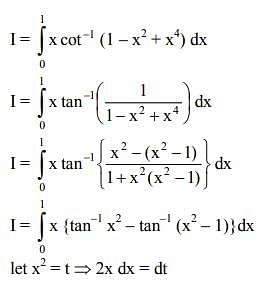
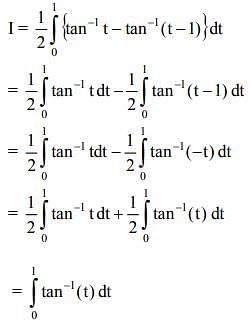
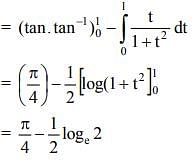
Q.27. The value of 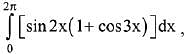 where [t] denotes the greatest integer function, is: (2019)
where [t] denotes the greatest integer function, is: (2019)
(1) π
(2) -π
(3) -2π
(4) 2π
Ans. (2)
Solution.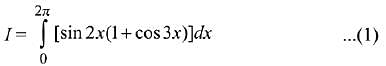
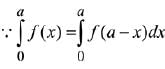
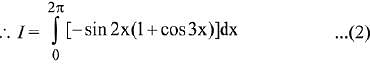
From (1) + (2), we get;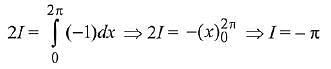
Q.28. 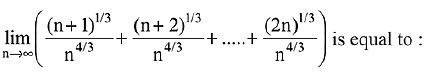 (2019)
(2019)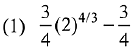
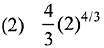
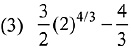
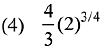
Ans. (1)
Solution.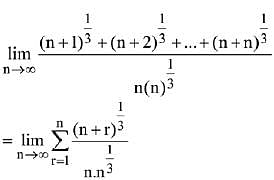
Q.29. is equal to: (2019)
is equal to: (2019)
(1) 35/6 - 32/3
(2) 34/3 - 31/3
(3) 37/6 - 35/6
(4) 35/3 - 31/3
Ans. (3)
Solution.
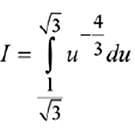
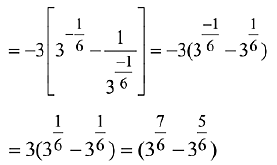
Q.30. 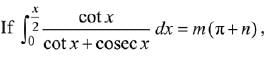 then m.n is equal to: (2019)
then m.n is equal to: (2019)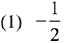
(2) 2
(3) 1/2
(4) -1
Ans. (4)
Solution.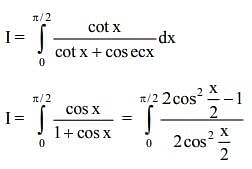
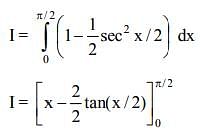
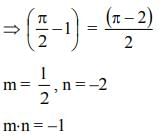
Q.31. A value of α such that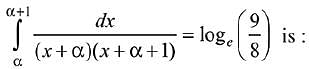 (2019)
(2019)
(1) -2
(2) 1/2
(3) 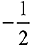
(4) 2
Ans. (1)
Solution.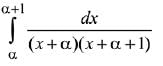
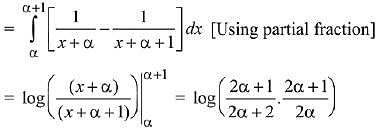
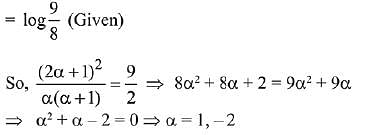
Q.32. The area (in sq. units) bounded by the parabola y = x2 - 1, the tangent at the point (2, 3) to it and the y-axis is: (2019)
(1) 8/3
(2) 32/3
(3) 56/3
(4) 14/3
Ans. (1)
Solution.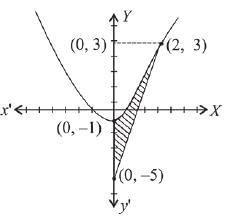
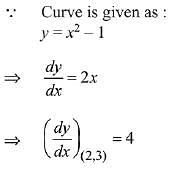
equation of tangent at (2, 3)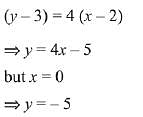
Here the curve cuts Y-axis
∴ required area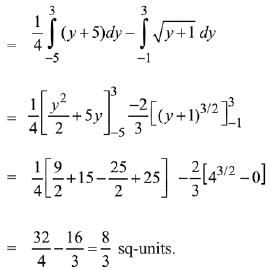
Q.33. The area of the region A = {(x, y): 0 ≤ y ≤ x |x| + 1 and - 1 ≤ x ≤ 1} in sq. units is: (2019)
(1) 2/3
(2) 2
(3) 4/3
(4) 1/3
Ans. (2)
Solution.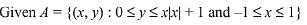
∴ Area of shaded region
Q.34. If the area enclosed between the curves y = kx2 and x = ky2, (k > 0), is 1 square unit. Then k is: (2019)
(1) √3/2
(2) 1/√3
(3) √3
(4) 2/√3
Ans. (2)
Solution.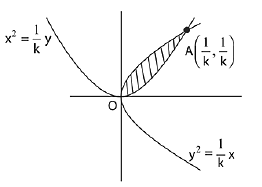
Two curves will intersect in the 1st quadrant at 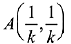
∵ area of shaded region = 1.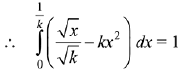
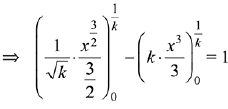
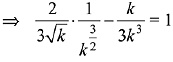
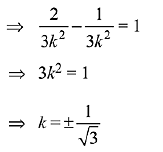

Q.35. The area (in sq. units) of the region bounded by the curve x2 = 4 y and the straight line x = 4y - 2 is: (2019)
(1) 5/4
(2) 9/8
(3) 7/8
(4) 3/4
Ans. (2)
Solution.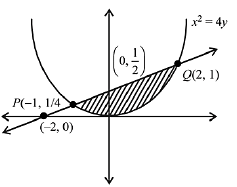
Let points of intersection of the curve and the line be P and Q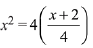
x2 - x - 2 = 0
x = 2, - 1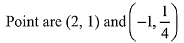
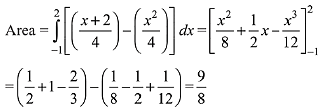
Q.36. The area (in sq. units) in the first quadrant bounded by the parabola,y = x2 + 1, the tangent to it at the point (2, 5) and the coordinate axes is: (2019)
(1) 8/3
(2) 37/24
(3) 187/24
(4) 14/3
Ans. (2)
Solution.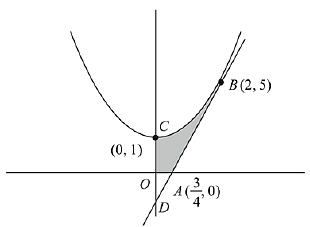
The equation of parabola x2 = y - 1
The equation of tangent at (2, 5) to parabola is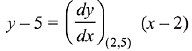
y - 5 = 4(x - 2)
4x - y = 3
Then, the required area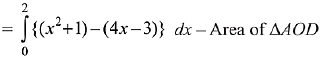
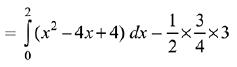
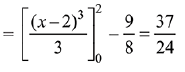
Q.37. The area (in sq. units) of the region bounded by the parabola, y = x2 + 2 and the lines, y = x + 1, x = 0 and x = 3, is: (2019)
(1) 15/4
(2) 21/2
(3) 17/4
(4) 15/2
Ans. (4)
Solution.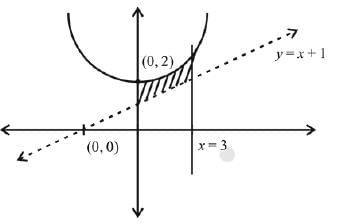
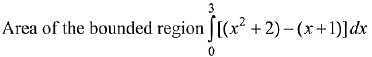
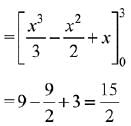
Q.38. The area (in sq. units) of the region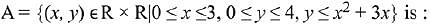 (2019)
(2019)
(1) 53/6
(2) 8
(3) 59/6
(4) 26/3
Ans. (3)
Solution.
Since, the relation y ≤ x2 + 3x represents the region below the parabola in the 1st quadrant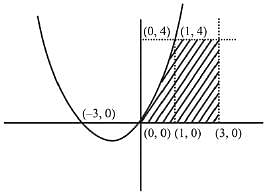
∵ y = 4
⇒ x2 + 3x = 4 ⇒ x = 1, -4
the required area = area of shaded region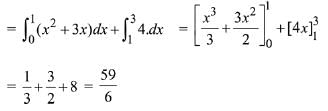
Q.39. Let S(α) = {{x, y): y2 ≤ x, 0 ≤ x ≤ α} and A(α) is area of the region S(α). If for a λ, 0 < λ < 4, A(λ) : A(4) = 2 : 5, then λ equals: (2019)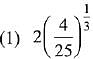
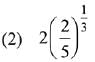
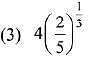
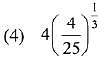
Ans. (4)
Solution.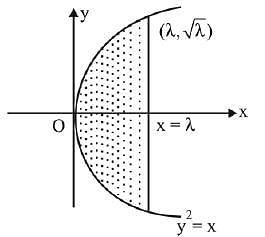
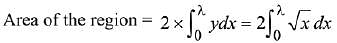
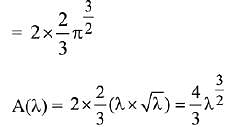
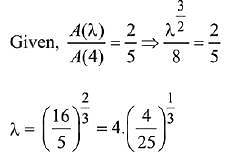
Q.40. The area (in sq. units) of the region A = {(x, y): x2 ≤ y ≤ x + 2} is: (2019)
(1) 10/3
(2) 9/2
(3) 31/6
(4) 13/6
Ans. (2)
Solution.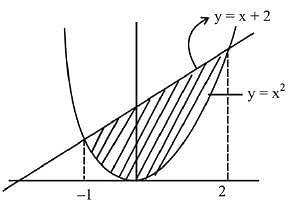
Required area is equal to the area under the curves y ≥ x2 and y ≤ x + 2
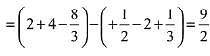
Q.41. The area (in sq. units) of the region 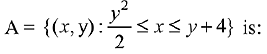 (2019)
(2019)
(1) 53/3
(2) 30
(3) 16
(4) 18
Ans. (4)
Solution.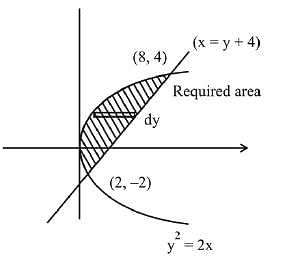
Q.42. The region represented by |x - y| ≤ 2 and |x + y|≤ 2 is bounded by a: (2019)
(1) square of side length 2√2 units
(2) rhombus of side length 2 units
(3) square of area 16 sq. units
(4) rhombus of area 8√2 sq. units
Ans. (1)
Solution.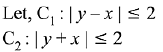
By the diagram, region is square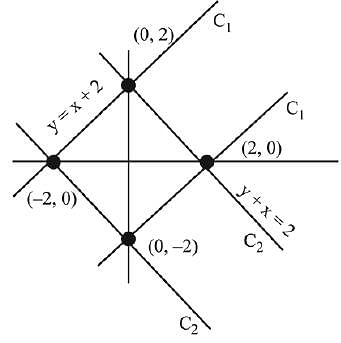
Q.43. The area (in sq. units) of the region bounded by the curves y = 2x and y = |x +1|, in the first quadrant is: (2019)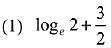
(2) 3/2
(3) 1/2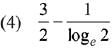
Ans. (4)
Solution.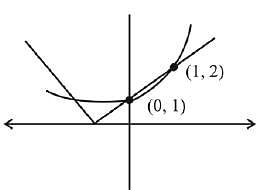
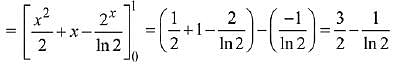
Q.44. If the area (in sq. units) of the region {(x, y) : y2 ≤ 4x, x + y ≤ 1, x ≥ 0, y ≥ 0} is a √2 + b, then a - b is equal to: (2019)
(1) 10/3
(2) 6
(3) 8/3
(4) -2/3
Ans. (2)
Solution.
Consider y2 = 4x and x + y = 1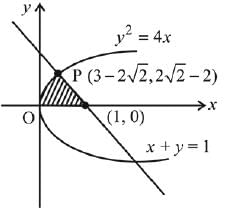
Substituting x = 1 - y in the equation of parabola,
y2 = 4(1 - y) ⇒ y2 + 4y - 4 = 0
⇒ (y + 2)2 = 8 ⇒ y + 2 = ±2√2
Hence, required area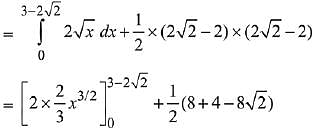
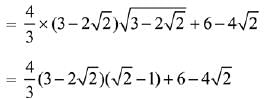
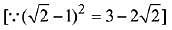
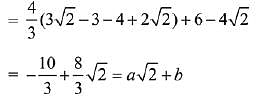
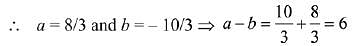
Q.45. If the area (in sq. units) bounded by the parabola y2 = 4λx and the line y = λx, λ > 0, is 1/9, then λ is equal to: (2019)
(1) 2√6
(2) 48
(3) 24
(4) 4√3
Ans. (3)
Solution.
Given parabola y2 = 4λx and the line y = λx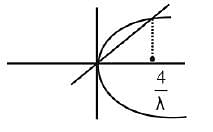
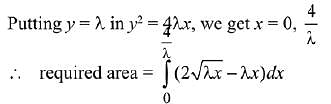
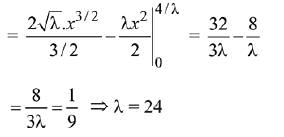
Q.46. The value of 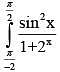 dx is: (2018)
dx is: (2018)
(1) π/8
(2) π/2
(3) 4π
(4) π/4
Ans. (4)
Solution.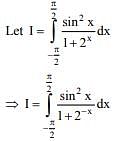
Q.47. Let g(x) = cos x2 ,f(x) = √x, and α ,β (α < β) be the roots of the quadratic equation 18x2 - 9πx +π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x =α , x = β and y = 0 , is: (2018)
(1)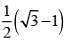
(2)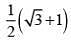
(3)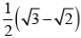
(4)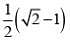
Ans. (1)
Solution.
g(x) = cos x2
f(x) = √x
g(f (x)) = cos x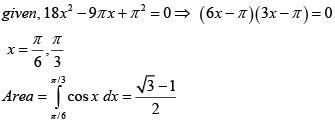
Q.48. The value of the integral 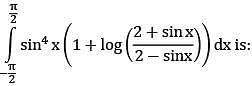 (2018)
(2018)
(1) 3/4
(2) 0
(3)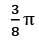
(4)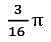
Ans. (4)
Solution.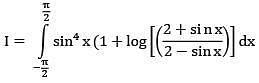
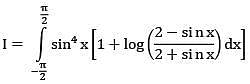
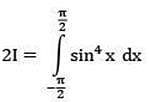
I = 3π/16
Q.49. The area (in sq. units) of the region {x ϵ R ∶ x ≥ 0, y ≥ x − 2 and y ≥ √x} is∶ (2018)
(1) 8/3
(2) 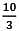
(3)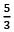
(4)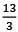
Ans. (2)
Solution.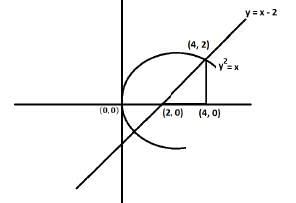
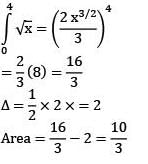
Q.50. If the area of the region bounded by the curves, y = x2, y = 1/x and the lines y = 0 and x = t (t > 1) is 1 sq. unit, then t is equal to: (2018)
(1) e2/3
(2) e3/2
(3) 3/2
(4) 4/3
Ans. (1)
Solution.
The intersection point of y = x2 and y = 1/x is (1, 1)
Area bounded by the curves is the region ABCDA is given as: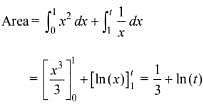
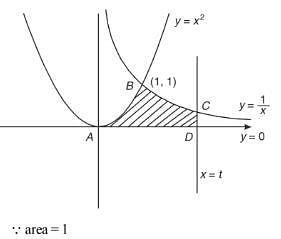
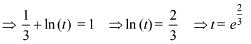
Q.51. The area (in sq. units) of the region {(x, y) : x ≥ 0, x + y ≤ 3, x2 ≤ 4y and y ≤ 1 + √x} is (2017)
(1) 5/2
(2) 59/12
(3) 3/2
(4) 7/3
Ans. (1)
Solution: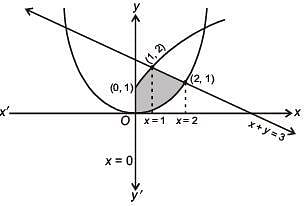
Area of shaded region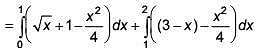
= 5/2 sq. unit
Q.52. The integral 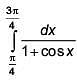 is equal to (2017)
is equal to (2017)
(1) –1
(2) –2
(3) 2
(4) 4
Ans. (3)
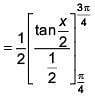
Solution: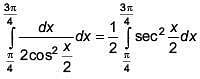
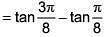
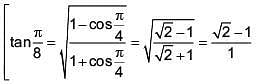
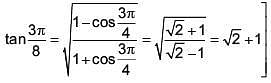
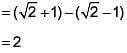
Q.53.  (2017)
(2017)
(1) 13/256
(2) 15/64
(3) 13/32
(4) 15/128
Ans. (4)
Solution.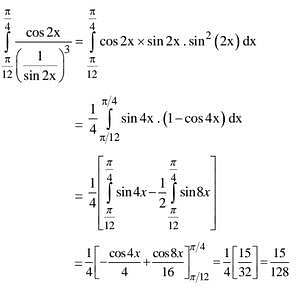
Q.54. The area (in sq. units) of the smaller portion enclosed between the curves, x2 + y2 = 4 and y2 = 3x, is: (2017)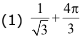



Ans. (1)
Solution.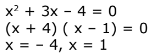


Q.55.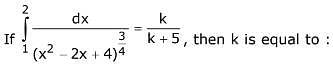 (2017)
(2017)
(1) 4
(2) 2
(3) 3
(4) 1
Ans. (4)
Solution.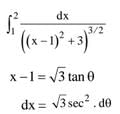
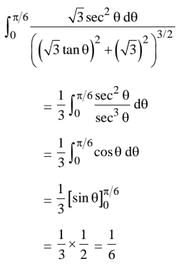
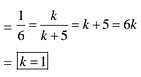
Q.56. The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is: (2016)
(1) 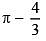
(2)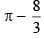
(3)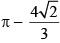
(4)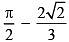
Ans. (2)
Solution.
x2 + y2 ≤ 4x & y2 ≥ 2x
To find point of intersection,
x2 + y2 = 4x ⇒ x2 + 2x = 4x
⇒ x2 - 2x = 0 ⇒ x (x - 2) = 0
⇒ x = 0 or x = 2
∴ y = 0 or y = 2
Solve (x, y) = (0, 0) & (x, y) = (2, 2)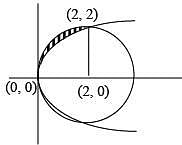
Area = 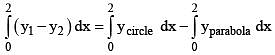
Q.57. (2016)
(2016)
(1) log 2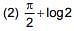
(3) log 4
(4) 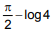
Ans. (1)
Solution.

Q.58. The area (in sq. units) of the region described by A = {(x, y) | y ≥ x2 - 5x + 4, x + y ≥ 1, y ≤ 0} is: (2016)
(1) 7/2
(2) 13/6
(3) 17/6
(4) 19/6
Ans. (4)
Solution.
A = {(x,y)|y ≥ x2 - 5x + 4, x + y ≥ 1, y ≤ 0}
Here y ≥ x2 - 5x + 4, x + y ≥ 1 , y ≤ 0

Q.59. For x ∈ R, x ≠ 0, if y(x) is a differentiable function such that  equals (2016)
equals (2016)
(where C is a constant) 



Ans. (4)
Solution.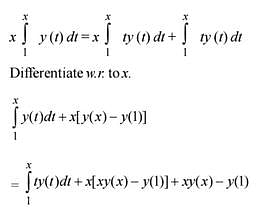
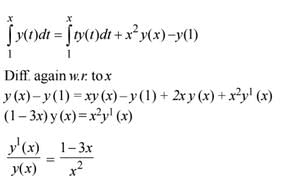
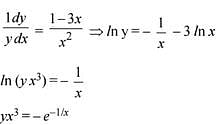
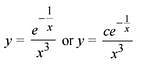
Q.60. The value of the integral 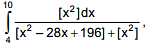 where [x] denotes the greatest integer less than or equal to x, is (2016)
where [x] denotes the greatest integer less than or equal to x, is (2016)
(1) 3
(2) 7
(3) 6
(4) 1/3
Ans. (1)
Solution.

|
149 videos|192 docs|197 tests
|


















