JEE Main Previous Year Questions (2016-2025): Differentiation | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. The number of real roots of the equation 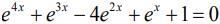 is (2020)
is (2020)
(1) 1
(2) 3
(3) 2
(4) 4
Ans. (1)
The given equation is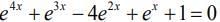
Let ex = t, so
Dividing both sides of the equation by t2,we get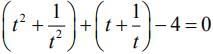
Again,
Let 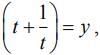
Then, y2 +y −3 =0 ⇒ (y − 2)(y +3) = 0
⇒ y = -2, 3
Now, 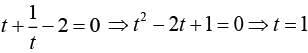 and
and 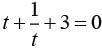 (not possible)
(not possible)
Hence, ex = 1 ⇒ x = 0
Q.2. If x = 2 sinθ - sin2θ and y = 2cosθ - cos2θ, θ∈[0,2π], then at θ = π is (2020)
(1) 3/4
(2) 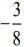
(3) 3/2
(4) 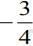
Ans. (Bonus)
We have,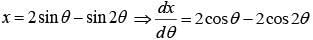 (1)
(1)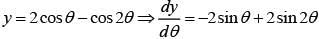 (2)
(2)
From Eqs. (1) and (2), we have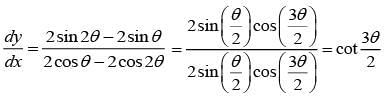
Now,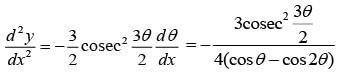

Q.3. If x = 3 tan t and y = 3 sec t, then the value of 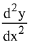 at t = π/4, is: (2019)
at t = π/4, is: (2019)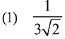
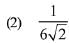
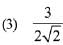
(4) 1/6
Ans. (2)
Solution.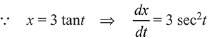
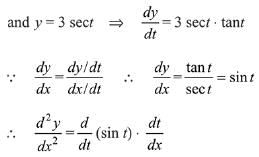

Q.4. Let f : R → R be a function such that f(x) = x3 + x2f'(1) + xf"(2) + f"'(3), x∈R Then f(2) equals: (2019)
(1) -4
(2) 30
(3) -2
(4) 8
Ans. (3)
Solution.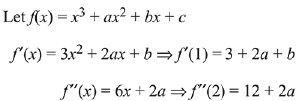
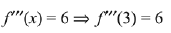
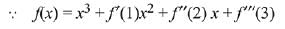
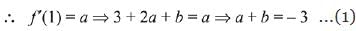
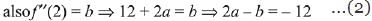
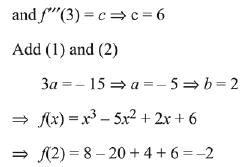
Q.5. If x loge (loge x) - x2 + y2 = 4(y > 0), then dy/dx at x = e is equal to: (2019)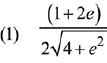
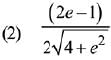
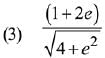
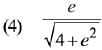
Ans. (2)
Solution. Consider the equation,
x loge (loge x) - x2 + y2 = 4
Differentiate both sides w.r.t. x,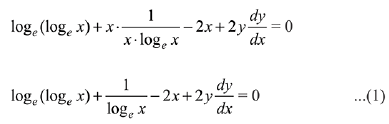

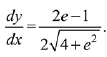
Q.6. For x > 1, if (2x)2y = 4e2x-2y, then (1 + loge 2x)2 dy/dx equal to: (2019)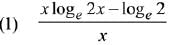
(2) loge 2x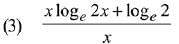
(4) x loge 2x
Ans. (1)
Solution.
(2x)2y = 4e2x-2y
⇒ 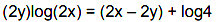

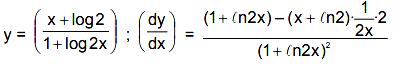
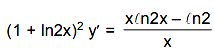
Q.7. Let f be a differentiable function such that f(1) = 2 and f' (x) = f(x) for all x ∈ R. If h (x) = f(f(x)), then h' (1) is equal to: (2019)
(1) 2e2
(2) 4e
(3) 2e
(4) 4e2
Ans. (2)
Solution.
Since, f'(x) = f(x)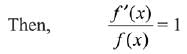
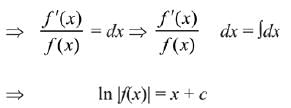
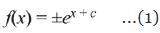
Since, the given condition
f(1) = 2
From eqn (1)
f(x) = ex+c = ecex
Then, f(1) = ec.e1
⇒ 2 = ec.e
⇒ 2/e = ec
Then, from eqn (1)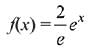
⇒ 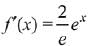
Now 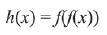
⇒ 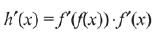

Q.8.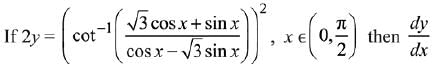 is equal to: (2019)
is equal to: (2019)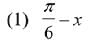
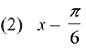
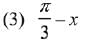
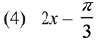
Ans. (Bouns)
Solution.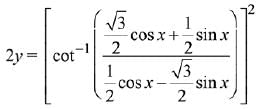
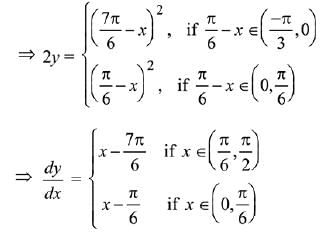
Q.9. If f(1) = 1, f'(1) = 3, then the derivative of f(f(f(x))) + (f(x))2 at x = 1 is: (2019)
(1) 33
(2) 12
(3) 15
(4) 9
Ans. (1)
Solution.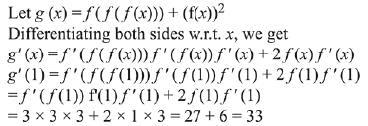
Q.10. If ey + xy = e, the ordered pair 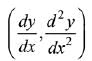 at x = 0 is equal to: (2019)
at x = 0 is equal to: (2019)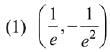
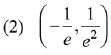
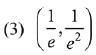
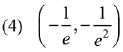
Ans. (2)
Solution.
Given, ey +xy = e ...(i)
Putting x = 0 in (i), ⇒ ey = e ⇒ y = 1
On differentiating (i) w. r. to x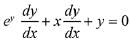 ...(ii)
...(ii)
Putting y = 1 and x= 0 in (ii),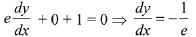
On differentiating (ii) w. r. to x,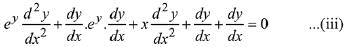
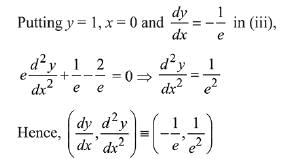
Q.11. The derivative of 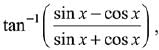 , with respect to x/2, where (2019)
, with respect to x/2, where (2019)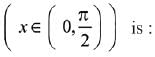
(1) 1
(2) 2/3
(3) 1/2
(4) 2
Ans. (4)
Solution.
Q.12. If 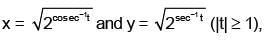 then dy/dx is equal to: (2018)
then dy/dx is equal to: (2018)
(1) y/x
(1) - y/x
(1) - x/y
(1) x/y
Ans: (2)
Solution: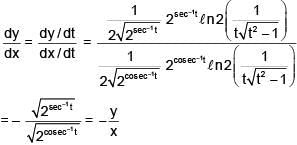
Q.13. If x2 + y2 + sin y = 4, then the value of d2y/dx2 at the point (-2, 0) is: (2017)
(1) -34
(2) -2
(3) 4
(4) -32
Ans: (1)
Solution: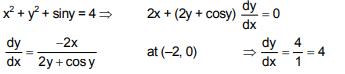

Q.14. Let f be a polynomial function such that f(3x) = f'(x). f"(x), for all x ∈ R. Then: (2017)
(1) f(2) + f'(2) = 28
(2) f"(2) - f'(2) = 0
(3) f(2) - f'(2) + f"(2) = 10
(4) f"(2) - f(2) = 4
Ans. (2)
Solution.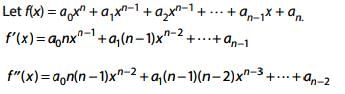
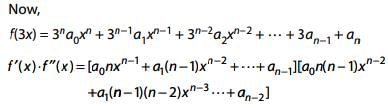
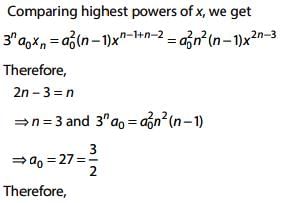
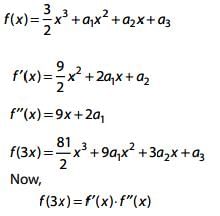
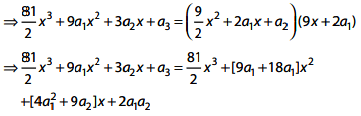

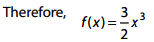
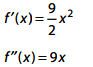
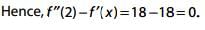
Q.15. For x ∈ R, x ≠ 0, x ≠ 1, let f0(x)= 1/1-x and fn + 1(x) = f0 (f(n(X)), n = 0, 1, 2, ....... Then the value of 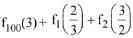 is equal to: (2016)
is equal to: (2016)
(1) 4/3
(2) 1/3
(3) 5/3
(4) 8/3
Ans. (3)
Solution.
We have
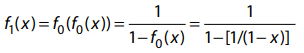
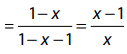
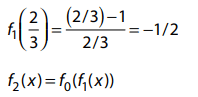


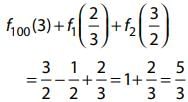
|
347 docs|185 tests
|





















