JEE Main Previous Year Questions (2016- 2024): Circle | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. Let the tangents drawn from the origin to the circle, x2+ y2 - 8x - 4y + 16 = 0 touch it at the points A and B. The (AB)2 is equal to (2020)
(1) 52/5
(2) 56/5
(3) 64/5
(4) 32/5
Ans. (3)
Solution. The equation of the given circle is
x2+ y2 - 8x - 4y + 16 = 0
Therefore,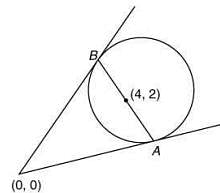
Radius of the circle, R = 
Length of tangent, L = √S1 = √16 = 4
Now, the length of chord AB = 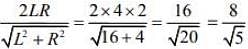
Hence, the square of length of chord is 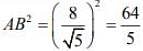
Q.2. If a line y = mx + c is a tangent to the circle (x - 3)2 + y2 = 1 and it is perpendicular to a line L1, where L1 is the tangent to the circle x2 + y2 = 1 at the point 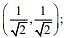 then (2020)
then (2020)
(1) c2 - 7c + 6 = 0
(2) c2 + 7c + 6 = 0
(3) c2 + 6c + 7 = 0
(4) c2 - 6c + 7 = 0
Ans. (3)
Solution.
Given, L1 is the tangent to the circle x2 + y2 = 1 at point (1/√2, 1/√2); so
Now, the slope of line y = mx + c is
m = -1/mL = 1
Therefore, y = x + c is tangent to (x - 3)2 + y2 = 1, so the length of perpendicular from the center (3, 0) to the tangent is equal to the radius of the circle.
Now, 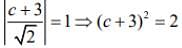
⇒ c2 + 6c + 7 = 0
Q.3. A circle touches the y-axis at the point (0, 4) and passes through the point (2, 0). Which of the following lines is not a tangent to this circle? (2020)
(1) 4x + 3y + 17 =0
(2) 3x + 4y - 24 = 0
(3) 3x + 4y - 6 = 0
(4) 4x + 3y - 8 = 0
Ans. (4)
Solution. We have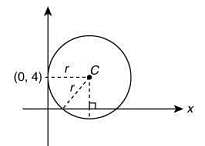
Therefore, the equation of the circle is
(x - 0)2 + (y - 4)2 + λx = 0 ...(1)
It passes through the (2,0) , then
4 + 16 + 2λ = 0 ⇒ λ = - 10
The equation of the circle is
x2 + y2 - 10x + 8y + 16 = 0
Hence, the radius of the circle is
⇒ 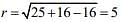
Now, the lengths of perpendicular drawn from the center (5,4) to the given lines are
Q.4. If the curves x2 - 6x + y2 + 8 = 0 and x2 - 8y + y2 +16 - k = 0, (k > 0) touch each other at a point, then the largest value of k is ________. (2020)
Ans. (36.00)
Solution. For the circle x2 - 6x + y2 +8 = 0, we have
C1 = (3, 0) and r1 =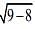 = 1
= 1
For the circle x2 - 8y + y2 + 16 - k = 0, we have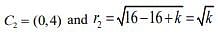
Two circles touch each other if C1C2 = |r1 ± r2|
⇒ k = 16 or 36
Q.5. Equation of a common tangent to the circle, x2 + y2 - 6x = 0 and the parabola, y2 = 4x, is: (2019)
(1) 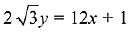
(2) 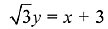
(3) 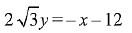
(4) 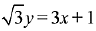
Ans. (2)
Solution. Since, the equation of tangent to parabola y2 = 4x is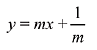 ...(1)
...(1)
The line (1) is also the tangent to circle
x2 + y2 - 6x = 0
Then centre of circle = (3, 0)
Radius of circle = 3
The perpendicular distance from centre to tangent is equal to the radius of circle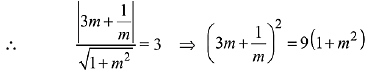
⇒ 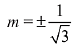
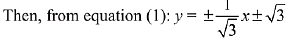
Hence, 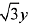 = x + 3 is one of the required common tangent.
= x + 3 is one of the required common tangent.
Q.6. Three circles of radii a, b, c (a < b < c) touch each other externally. If they have x-axis as a common tangent, then: (2019)
(1) 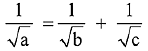
(2) 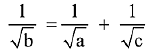
(3) a, b, c are in A.P
(4) 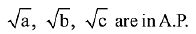
Ans. (1)
Solution.

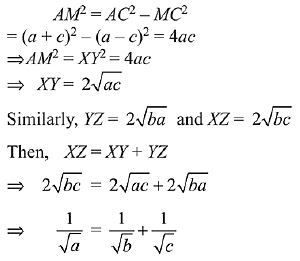
Q.7. If the circles x2 + y2 - 16x - 20y + 164 = r2 and (x - 4) + (y - 7)2 = 36 intersect at two distinct points, then: (2019)
(1) r > 11
(2) 0 < r < 1
(3) r = 11
(4) 1 < r < 11
Ans. (4)
Solution. Consider the equation of circles as,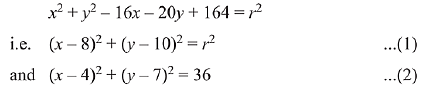
Both the circles intersect each other at two distinct points. Distance between centres
Q.8. If a circle C passing through the point (4, 0) touches the circle x2 + y2 + 4x - 6y = 12 externally at the point (1, -1), then the radius of C is: (2019)
(1) 2√5
(2) 4
(3) 5
(4) √57
Ans. (3)
Solution. The equation of circle x2 + y2 + 4x - 6y = 12 can be written as (x + 2)2 + (y - 3)2 = 25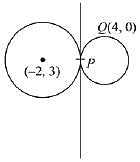
Let P = (1, -1) & Q = (4, 0)
Equation of tangent at P (1, -1) to the given circle:
x(1) + y(-1) + 2(x+1) - 3(y-1) - 12 = 0
3x - 4y - 7 = 0 ...(1)
The required circle is tangent to (1) at (1, -1).
∴ (x-1)2 + (y+1)2 + λ(3x-4y-7) = 0 ...(2)
Equation (2) passes through Q(4, 0)
⇒ 32+12+λ(12-7) = 0 ⇒ 5λ+10 = 0
⇒ λ = -2
Equation (2) becomes x2 + y2 - 8x + 10y + 16 = 0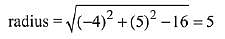
Q.9. If the area of an equilateral triangle inscribed in the circle, x2 + y2 + 10x + 12y + c = 0 is 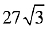 sq. units then c is equal to: (2019)
sq. units then c is equal to: (2019)
(1) 13
(2) 20
(3) -25
(4) 25
Ans. (4)
Solution.
Let the sides of equilateral Δ inscribed in the circle be a, then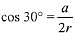
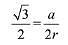
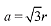
Then, area of the equilateral triangle 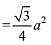
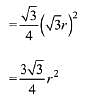
But it is given that area of equilateral triangle
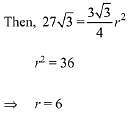
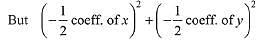 - constant term = r2
- constant term = r2
(-5)2 + (-6)2 - c = 36
c = 25
Q.10. A square is inscribed in the circle x2 + y2 - 6x + 8y - 103 = 0 with its sides parallel to the coordinate axes. Then the distance of the vertex of this square which is nearest to the origin is: (2019)
(1) 6
(2)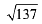
(3)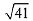
(4) 13
Ans. (3)
Solution. The equation of circle is,
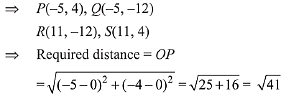
Q.11. Two circles with equal radii are intersecting at the points (0, 1) and (0, -1). The tangent at the point (0, 1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is: (2019)
(1) 1
(2) 2
(3) 2√2
(4) √2
Ans. (2)
Solution.
∵ Two circles of equal radii intersect each other orthogonally. Then R is mid point of PQ.
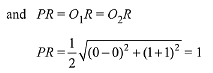
∴ Distance between centres = 1 + 1 = 2.
Q.12. A circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distant 2b from the origin. Then the locus of the centre of this circle, is: (2019)
(1) a hyperbola
(2) an ellipse
(3) a straight line
(4) a parabola
Ans. (4)
Solution.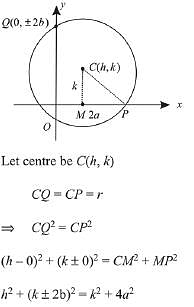
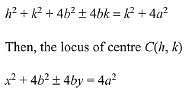
Hence, the above locus of the centre of circle is a parabola.
Q.13. Let C1 and C2 be the centres of the circles x2 + y2 - 2x - 2y - 2 = 0 and x2 + y2 - 6x - 6y + 14 = 0 respectively. If P and Q are the points of intersection of these circles then, the area (in sq. units) of the quadrilateral PC1QC2 is: (2019)
(1) 8
(2) 6
(3) 9
(4) 4
Ans. (4)
Solution.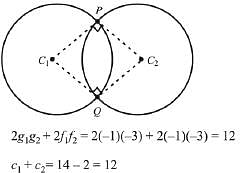
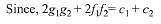
Hence, circles intersect orthogonally
∴ Area of the quadrilateral PC1QC1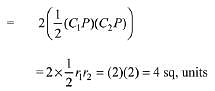
Q.14. If a variable line, 3x + 4y - λ = 0 is such that the two circles x2 + y2 - 2x - 2y + 1 =0 and x2 + y2- 18x - 2y + 78 = 0 are on its opposite sides, then the set of all values of λ is the interval: (2019)
(1) (2,17)
(2) [13,23]
(3) [12,21]
(4) (23,31)
Ans. (3)
Solution.
Condition 1: The centre of the two circles are (1, 1) and (9, 1). The circles are on opposite sides of the line 3x + 4y - λ = 0.
Put x = 1, y = 1 in the equation of line,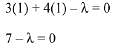
Now, put x = 9, y = 1 in the equation of line,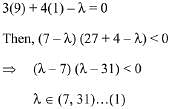
Condition 2: Perpendicular distance from centre on line ≥ radius of circle.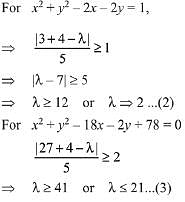
Intersection of (1), (2) and (3) gives λ ∈ [12, 21].
Q.15. If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is: (2019)
(1)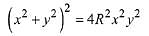
(2) 
(3) 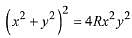
(4) 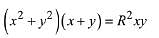
Ans. (2)
Solution. As ∠AOB = 90°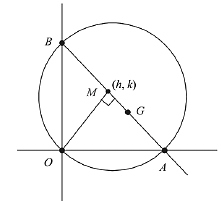
Let AB diameter and M(h, k) be foot of perpendicular, then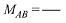
Then, equation of AB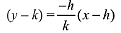

∴ AB is the diameter, then
AB = 2R
⇒ AB2 = 4R2
Hence, required locus is (x2 + y2)3 = 4R2 x2 y2
Q.16. The sum of the squares of the lengths of the chords intercepted on the circle, x2 + y2 = 16, by the lines, x + y = n, n∈N, where N is the set of all natural numbers, is: (2019)
(1) 320
(2) 105
(3) 160
(4) 210
Ans. (4)
Solution. Let the chord x + y = n cuts the circle x2 + y2 = 16 at P and Q Length of perpendicular from O on PQ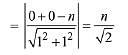
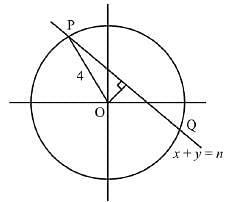
Then, length of chord 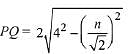
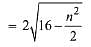
Thus only possible values of n are 1, 2, 3, 4, 5.
Hence, the sum of squares of lengths of chords
Q.17. The tangent and the normal lines at the point (√3, 1) to the circle x2 + y2 = 4 and the x-axis form a triangle. The area of this triangle (in square units) is: (2019)
(1) 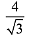
(2) 1/3
(3) 
(4) 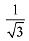
Ans. (3)
Solution. 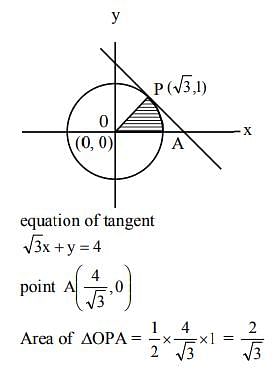
Q.18. If a tangent to the circle x2 + y2 - 1 intersects the coordinate axes at distinct points P and Q, then the locus of the midpoint of PQ is: (2019)
(1) x2 + y2 - 4x2y2 = 0
(2) x2 + y2 - 2xy = 0
(3) x2 + y2 - 16x2y2 = 0
(4) x2 + y2 - 2x2y2 = 0
Ans. (1)
Solution. Let any tangent to circle x2 + y2 = 1 is
x cosθ + y sinθ = 1
Since, P and Q are the point of intersection on the coordinate axes.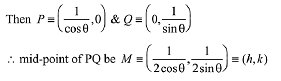
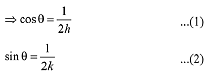
Now squaring and adding equation (1) and (2)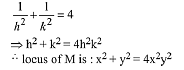
Q.19. The common tangent to the circles x2 + y2 = 4 and x2 + y2 + 6x + 8y - 24 = 0 also passes through the point: (2019)
(1) (4,-2)
(2) (-6,4)
(3) (6,-2)
(4) (-4,6)
Ans. (3)
Solution. By the diagram, 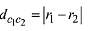
Equation of common tangent is,
S1 - S2 = 0
6x + 8y - 20 = 0
⇒ 3x + 4y - 10 = 0
Hence (6, -2) lies on it.
Q.20. If the circles x2 + y2 + 5Kx + 2y + K = 0 and 2(x2 + y2) + 2Kx + 3y - 1=0, (K∈R), intersect at the points P and Q, then the line 4x + 5y - K = 0 passes through P and Q, for: (2019)
(1) infinitely many values of K
(2) no value of K.
(3) exactly two values of K
(4) exactly one value of K
Ans. (2)
Solution.
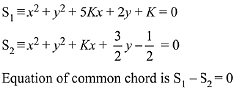
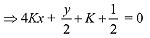 ...(1)
...(1)
Equation of the line passing through the intersection points P & O is.
4x + 5y - K = 0 ...(2)
Comparing (1) and (2),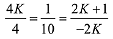 ...(3)
...(3)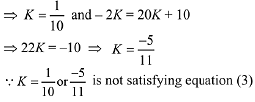
∴ No value of K exists.
Q.21. The line x = y touches a circle at the point (1, 1). If the circle also passes through the point (1, -3), then its radius is: (2019)
(1) 3
(2) 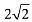
(3) 2
(4) 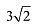
Ans. (2)
Solution. Equation of circle which touches the line y = x at (1,1) is, (x-1)2 + (y-1)2 + λ(y-x) = 0
This circle passes through (1,-3)
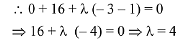
Hence, equation of circle will be,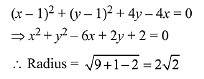
Q.22. The locus of the centres of the circles, which touch the circle, x2 + y2 = 1 externally, also touch the y-axis and lie in the first quadrant, is: (2019)
(1) 
(2) 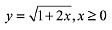
(3) 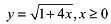
(4) 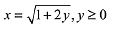
Ans. (2)
Solution. Let centre of required circle is (h, k).
∴ OO' = r + r' [By the diagram]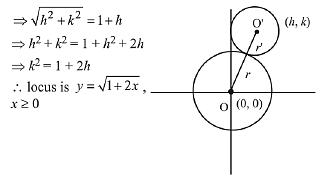
Q.23. If the angle of intersection at a point where the two circles with radii 5 cm and 12 cm intersect is 90°, then the length (in cm) of their common chord is: (2019)
(1) 13/5
(2) 120/13
(3) 60/13
(4) 13/2
Ans. (2)
Solution.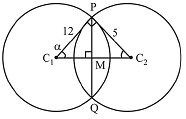
According to the diagram,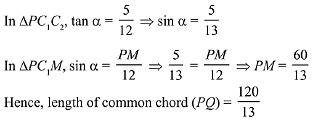
Q.24. A circle touching the x-axis at (3,0) and making an intercept of length 8 on the y-axis passes through the point: (2019)
(1) (3,10)
(2) (3,5)
(3) (2,3)
(4) (1,5)
Ans. (1)
Solution. Let centre of circle is C and circle cuts the v-axis at B and A. Let mid-point of chord BA is M.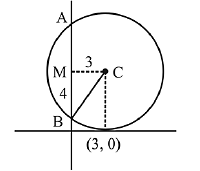
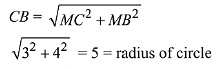
equation of circle is,
(x - 3)2 + (y - 5)2 = 52
(3, 10) satisfies this equation.
Although there will be another circle satisfying the same conditions that will lie below the x-axis having equation (x - 3)2 + (y - 5)2 = 52
Q.25. Let the orthocenter and centroid of a triangle be A(-3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, than the radius of the circle having line segment AC as diameter, is: (2018)
(1) √10
(2) 2√10
(3) 
(4) 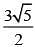
Ans. (3)
Solution. Orthocentre A (-3, 5) centroid B (3, 3)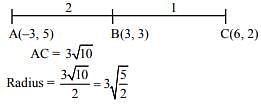
Q.26. If the tangent at (1,7) to the curve x2 = y - 6 touches the circle x2 + y2 + 16x + 12y + c = 0 than the value of c is: (2018)
(1) 195
(2) 185
(3) 85
(4) 95
Ans. (4)
Solution. Equation tangent at (1, 7)
⇒ 2x - y + 5 = 0
perpendicular (-8, -6) to line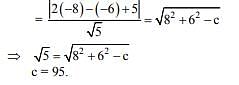
Q.27. A circle passes through the points (2, 3) and (4, 5). If its centre lies on the line, y - 4x + 3 = 0, then its radius is equal to: (2018)
(1) √5
(2) 2
(3) √2
(4) 1
Ans. (2)
Solution. Let centre of circle is c(α,β)
it lies is line y – 4x + 3 = 0 B = 4α – 3
∴ c(α, 4α–3)
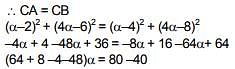
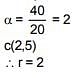
Q.28. If a circle C, whose radius is 3, touches externally the circle, x2 + y2 + 2x – 4y – 4 = 0 at the point (2, 2), then the length of the intercept cut by this circle C, on the x-axis is equal to: (2018)
(1) 2√3
(2) √5
(3) 3√2
(4) 2√5
Ans. (4)
Solution.
Q.29. If a point P has co - ordinates ( 0,–2) and Q ia any point on the circle, x2 + y2 – 5x – y + 5 = 0, then the maximum value of (PQ)2 is: (2017)
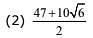
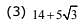
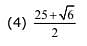
Ans. (3)
Solution.
The center of the circle 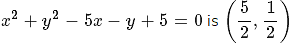 and radius is
and radius is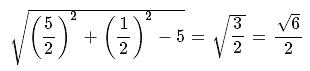
Let us put the values of the corrdinates of P(0,-2) in the LHS of the equation of circle 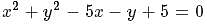 , we get
, we get 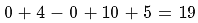 and as it is is greater than 0, the point is outside the circle and maximum distance of P from any point on the circle would be, distance of P from centrer of circle plus radius.
and as it is is greater than 0, the point is outside the circle and maximum distance of P from any point on the circle would be, distance of P from centrer of circle plus radius.
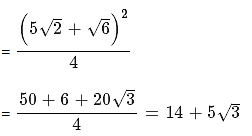
Q.30. If two parallel chords of the a circle, having diameter 4 units, lie on the opposite sides of the centre and subtend angles  and sec–1 (7) at the centre respectively, then the distance between these chords, is: (2017)
and sec–1 (7) at the centre respectively, then the distance between these chords, is: (2017)
(2) 16/7
(4) 8/7
Ans. (1)
Solution.
Distance between chords
= Radius Cos(subtended angle/2) by chord1 + Radius Cos(subtended angle/2) by chord 2
Radius = Diameter /2 = 4/2 = 2
= 2 Cos (θ₁/2) + 2Cos(θ₂/2)
θ₁ = Cos⁻¹(1/7) => Cosθ₁ = 1/7
θ₂ = Sec⁻¹7 => Secθ₂ = 7 => 1/Cosθ₂ = 7 => Cosθ₂ = 1/7
Applying Cos2θ = 2Cos²θ - 1 => Cos²θ = (1 + cos2θ)/2
Putting θ = θ₁/2
Cos²(θ₁/2) = ( 1 + 1/7)/2 = 4/4
=> Cos(θ₁/2) = 2/√7
Putting θ = θ₂/2
Cos²(θ₂/2) = ( 1 + 1/7)/2 = 4/7
=> Cos(θ₁/2) = 2/√7
2 Cos (θ₁/2) + 2Cos(θ₂/2) = 2 *2/√7 + 2 * 2/√7
= 4/√7 + 4/√7
= 8/√7
Q.31. A line drawn through the point P(4,7) cuts the circle x2+y2 = 9 at the points A and B. Then PA.PB is equal to: (2017)
(1) 74
(2) 53
(3) 56
(4) 65
Ans. (3)
Solution.
Length of a tangent from external point (x1,y1) = 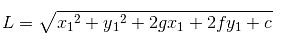
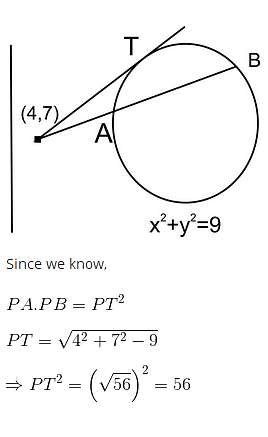
Q.32. The centres of those circles which touch the circle, x2 + y2 - 8x - 8y - 4 = 0, externally and also touch the x-axis, lie on: (2016)
(1) a circle
(2) an ellipse which is not a circle
(3) a hyperbola
(4) a parabola
Ans. (4)
x2 + y2 - 8x - 8y - 4 = 0
Centre (4, 4)
Radius = 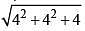 = 6
= 6
Let centre of the circle is (h, k) 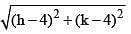 = (6 + k)
= (6 + k)
(h - 4)2 + (k - 4)2 = (6 + k)2
h2 - 8h + 16 + k2 - 8k + 16 = 36 + k2 + 12k
h2 - 8h - 20k - 4 = 0
x2 - 8x - 20y - 4 = 0
Which is an equation of parabola
Q.33. If one of the diameters of the circle, given by the equation, x2 + y2 - 4x + 6y - 12 = 0, is a chord of a circle S, whose centre is at (-3, 2), then the radius of S is: (2016)
(1) 5√2
(2) 5√3
(3) 5
(4) 10
Ans. (2)
x2 + y2 - 4x + 6y - 12 = 0
Centre (2, -3)
Radius 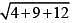 = 5
= 5
Distance b/w two centres c1(2, -3) and c2(-3, 2)
d = 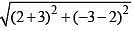 = √50
= √50
Radius of (S) = 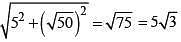
Q.34. A circle passes through (-2, 4). Which one of the following equations can represent a diameter of this circle? (2016)
(1) 4x + 5y - 6 = 0
(2) 5x + 2y + 4 = 0
(3) 2x - 3y + 10 = 0
(4) 3x + 4y - 3 = 0
Ans. (3)
Required circle is
(x - 0)2 + (y - 2)2 + λ(x) = 0
it passes (-2, 4)
∴ 4 + 4 - 2λ = 0
λ = 4
∴ circle is x2 + y2 - 4y + 4x + 4 = 0
centre (-2, 2) which satisfy
2x - 3y + 10 = 0
Q.35. Equation of the tangent to the circle, at the point (1, -1), whose centre is the point of intersection of the straight lines x - y = 1 and 2x + y = 3 is (2016)
(1) 3x - y - 4 = 0
(2) x + 4y + 3 = 0
(3) x - 3y - 4 = 0
(4) 4x + y - 3 = 0
Ans. (2)
Centre of circle is 
⇒ equation of circle is 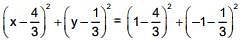
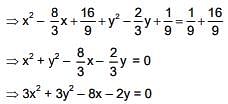
Equation of tangent at (1, -1) is 3x - 3y - 4(x + 1) - (y - 1) = 0
⇒ - x - 4y - 3 = 0
⇒ x + 4y + 3 = 0
|
149 videos|192 docs|197 tests
|



















