JEE Main Previous Year Questions (2016- 2025): Limits, Continuity and Differentiability | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. Let the function, f :[ 7,0] → 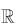 be continuous on [−7, 0] and differentiable on (−7, 0). If f (−7) = −3 and f'(x) < for all x ∈(-7, 0), then for all such functions f, f(-1) + f(0) lies in the interval (2020)
be continuous on [−7, 0] and differentiable on (−7, 0). If f (−7) = −3 and f'(x) < for all x ∈(-7, 0), then for all such functions f, f(-1) + f(0) lies in the interval (2020)
(1) (-∞ , 20]
(2) [ -3,11]
(3) ( -∞ ,11]
(4) [ -6, 20]
Ans. (1)
Using LMVT in [ -7, -1], we get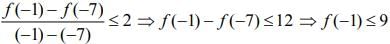 .....(1)
.....(1)
Using LMVT in [ -7, -0], we get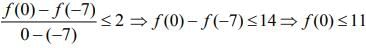 ....(2)
....(2)
From Eqs. (1) and (2), we get f(0) + f(-1) < 20
Q.2. Let S be the set of points where the function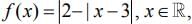 is not differentiable. Then
is not differentiable. Then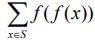 is equal to ________. (2020)
is equal to ________. (2020)
Ans. (3.00)
We have,
f (x) = 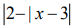
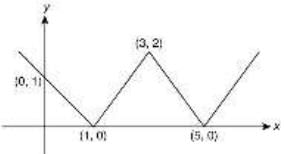
It is clear from the graph that the function is not differentiable at x =1,3 and 5.
Now, 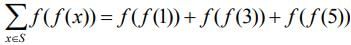
= f(0) + f(2) + f (0) = 1 + 1 + 1 = 3
Q.3. The value of c in the Lagrange’s mean value theorem for the function f(x) = x3 - 4x2 + 8x + 11, when x ∈[0,1] is (2020)
(1) 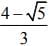
(2) 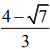
(3) 2/3
(4) 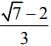
Ans. (2)
f(x) is a polynomial function, so it is continuous and differentiable in [0,1].
Now, f(x) = x3 - 4x2 + 8x + 11 ⇒ f'(x) = 3x2 - 8x + 8
f(0) = 11 and f(1) = 1 − 4 + 8 + 11 = 16
Using Lagrange’s mean value theorem, we get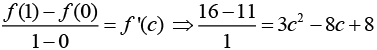

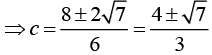
Now,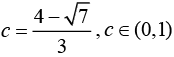
Q.4. If the function f defined on 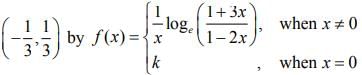 is continuous, then k is equal to ________. (2020)
is continuous, then k is equal to ________. (2020)
Ans. (5.00)
We have,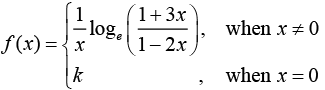
The function is continuous, then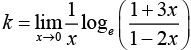
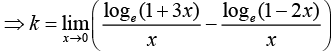
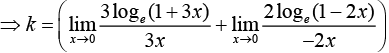
⇒ k =3+2 =5
Q.5. If c is a point at which Rolle’s theorem holds for the function 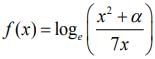 in the interval [3, 4], where
in the interval [3, 4], where 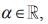 then f"(c) is equal to (2020)
then f"(c) is equal to (2020)
(1)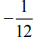
(2)1/12
(3) 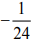
(4)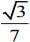
Ans. (2)
Given, Rolle’s theorem holds for the function 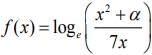 in the interval [3, 4], Then,
in the interval [3, 4], Then,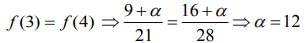
Now,
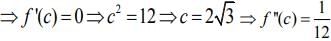
Q.6. Let S be the set of all functions f : [0,1] → which are continuous on [0, 1] and differentiable on (0, 1). Then for every f in S, there exists a c ∈(0,1), depending on f, such that (2020)
which are continuous on [0, 1] and differentiable on (0, 1). Then for every f in S, there exists a c ∈(0,1), depending on f, such that (2020)
(1) 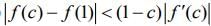
(2) 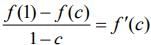
(3)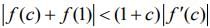
(4) 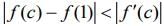
Ans. (Bonus)
S is a set of all functions
If we consider a constant function, then option 1, 3 and 4 are incorrect.
For option 2: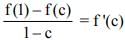
This may not be true for all the function
If we apply LMVT in (c, 1) then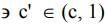 such that
such that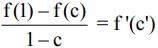
None of the option are incorrect
Q.7. Let f be any function continuous on [a,b] and twice differentiable on (a,b). If for all 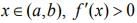 and f"(x)< 0, then for any
and f"(x)< 0, then for any  is greater than (2020)
is greater than (2020)
(1)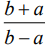
(2) 1
(3) 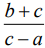
(4)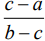
Ans. (4)
Using LMVT for we get
we get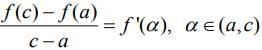
Also, using LMVT for x ∈ [c,b], we get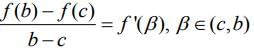
Since f"(x)< 0, then f'(x) is decreasing. Hence,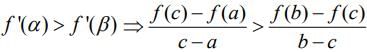
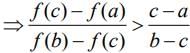
Q.8. If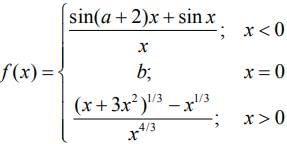 is continuous at x = 0, then a + 2b is equal to (2020)
is continuous at x = 0, then a + 2b is equal to (2020)
(1) 1
(2) -1
(3) 0
(4) -2
Ans. (3)
Given, the function f(x) is continuous at x = 0, then
f(0-) = f(0) = f(0+)
Therefore,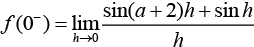
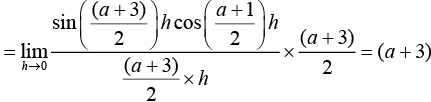
Now, 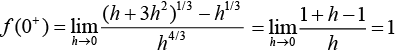
Therefore, a + 3 = b = 1 ⇒ a = -2 and b = 1
⇒ a+2b = −2+2= 0
Q.9. Let [t] denote the greatest integer ≤ t and 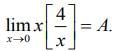 Then, the function f(x) = [x2]sin(πx) is discontinuous, when x is equal to (2020)
Then, the function f(x) = [x2]sin(πx) is discontinuous, when x is equal to (2020)
(1)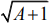
(2)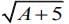
(3)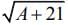
(4) 
Ans. (1)
We have,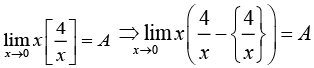
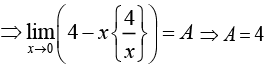
On solving options (2),(3) and (4), we obtain the integer values and integral multiple of π in sin is always zero.
For option (1), we get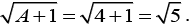 Hence, f (x) is discontinuous at x =
Hence, f (x) is discontinuous at x = 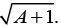
Q.10. Let  (a, k >0)
(a, k >0) 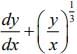 =0, then k is (2020)
=0, then k is (2020)
(1) 3/2
(2) 4/3
(3) 2/3
(4) 1/3
Ans. (3)
Given,
xk + yk = ak , (a, k > 0)... (1)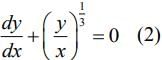
Now, using Eq. (1), we get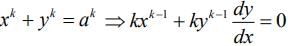
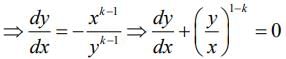
On comparing with Eq. (2), we get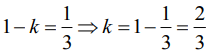
Q.11. 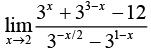 is equal t0 _______. (2020)
is equal t0 _______. (2020)
Ans. (36.00)
Given
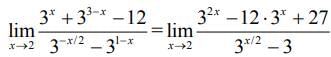
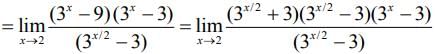
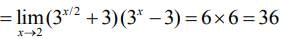
Q.12. Let y = y (x) be a function of x satisfying 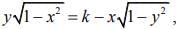 where k is a constant and
where k is a constant and 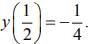
Then 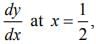 is equal to (2020)
is equal to (2020)
(1) 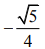
(2)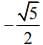
(3)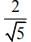
(4)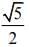
Ans. (2)
Given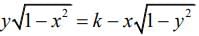
Let x = sin θ and y = sin ϕ, then the equation becomes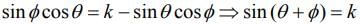
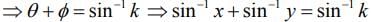 .....(1)
.....(1)
Differentiating Eq. (1) w.r.t. x, we get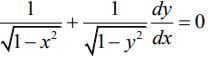

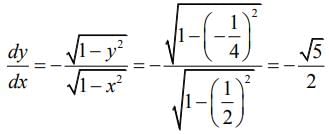
Q.13.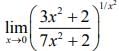 is equal to (2020)
is equal to (2020)
(1) 1/e
(2) 1/e2
(3) e2
(4) e
Ans. (2)
We have,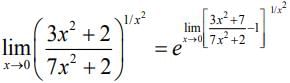
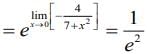
Q.14. Let f(x) = (sin(tan-1 x) + sin (cot-1 x))2 -1,  and
and 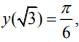 then
then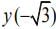 is equal to (2020)
is equal to (2020)
(1) 2π/3
(2) 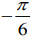
(3) 5π/6
(4) π/3
Ans. (3)
Let tan-1 x =θ ⇒ x = tanθ ⇒ 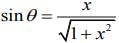
Now, 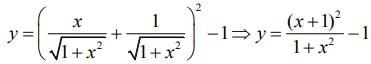
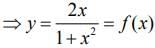
Now,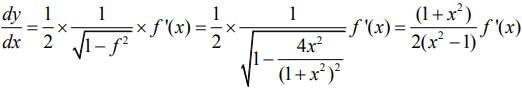
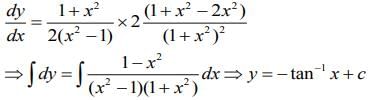
Given,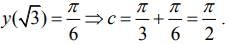
Therefore,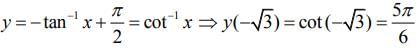
Q.15. 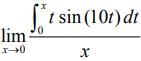 is equal to (2020)
is equal to (2020)
(1) 0
(2) 1/10
(3)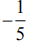
(4)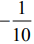
Ans. (1)
We have,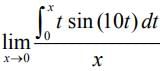
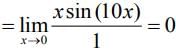 ....(using L Hospital rule)
....(using L Hospital rule)
Q.16. 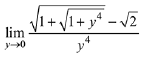 (2019)
(2019)
(1) exists and equals 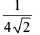
(2) exists and equals 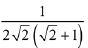
(3) exists and equals 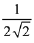
(4) does not exist
Ans. (1)
Solution.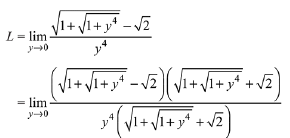
Q.17. For each x∈R, let [x] be greatest integer less than or equal to x. Then
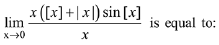 (2019)
(2019)
(1) - sin 1
(2) 1
(3) sin 1
(4) 0
Ans. (1)
Solution.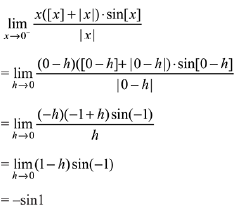
Q.18. For each t∈R, let [t] be the greatest integer less than or equal to t. Then,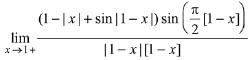 (2019)
(2019)
(1) equals 1
(2) equals 0
(3) equals - 1
(4) does not exist
Ans. (2)
Solution.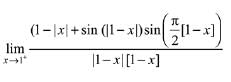
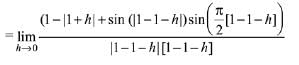
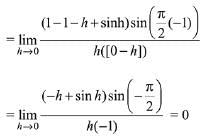
Q.19. Let f : R → R be a function defined as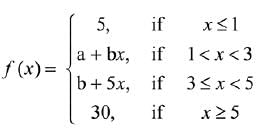
Then, f is: (2019)
(1) continuous if a = 5 and b = 5
(2) continuous if a = - 5 and b = 10
(3) continuous if a = 0 and b = 5
(4) not continuous for any values of a and b
Ans. (4)
Solution.
Let f(x) is continuous at x = 1, then
f(1-) = f(1) = f(1+)
⇒ 5 = a + b ...(1)
Let f(x) is continuous at x = 3, then
f(3-) = f(3) = f(3+)
⇒ a + 3b = b + 15 ...(2)
Let f(x) is continuous at x = 5, then
f(5-) = f(5) = f(5+)
⇒ b + 25 = 30
⇒ b = 30 - 25 = 5
From (1), a = 0
But a = 0, b = 5 do not satisfy equation (2)
Hence, f(x) is not continuous for any values of a and b
Q.20.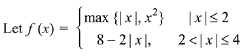
Let S be the set of points in the interval (- 4, 4) at which f is not differentiable. Then S: (2019)
(1) is an empty set
(2) equals {- 2, - 1, 0, 1, 2}
(3) equals {-2, - 1, 1, 2}
(4) equals {-2,2}
Ans. (2)
Solution.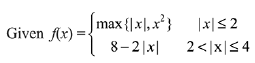
∵ f(x) is not differentiable at -2, -1,0, 1 and 2.
∴ S = {-2,-1,0, 1,2}
Q.21. Let f be a differentiable function such that f'(x) 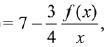 (x > 0) and f'(1) ≠ 4. Then
(x > 0) and f'(1) ≠ 4. Then 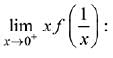 (2019)
(2019)
(1) exists and equals 4/7.
(2) exists and equals 4.
(3) does not exist.
(4) exists and equals 0.
Ans. (2)
Solution. Let y = f(x)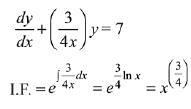
Solution of differential equation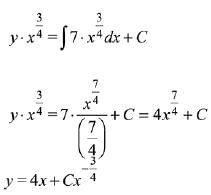
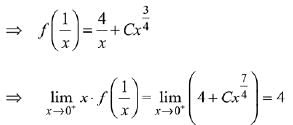
Q.22. Let [x] denote the greatest integer less than or equal to x. Then: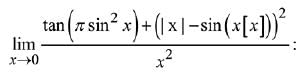 (2019)
(2019)
(1) does not exist
(2) equals π
(3) equals π + 1
(e) equals 0
Ans. (1)
Solution.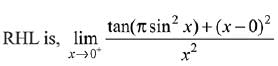
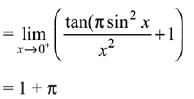
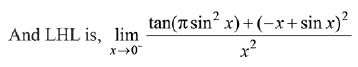
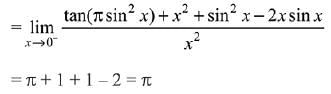
Since, LHL ≠ RHL
Hence, limit does not exist.
Q.23. 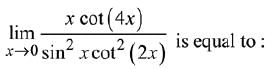 (2019)
(2019)
(1) 0
(2) 2
(3) 4
(4) 1
Ans. (4)
Solution.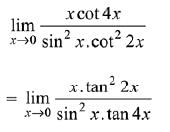
Q.24. Let f = R → R be differentiable at c ∈ R and f (c) = 0. If g (x) = |f(x)|, then at x = c, g is: (2019)
(1) not differentiable if f' (c) = 0
(2) differentiable if f’(c) ≠ 0
(3) differentiable if f’(c) = 0
(4) not differentiable
Ans. (3)
Solution.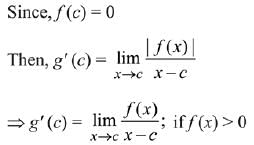
Q.25.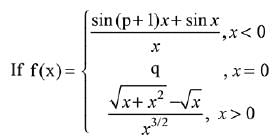
is continuous at x = 0, then the ordered pair (p, q) is equal to: (2019)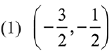
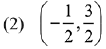
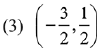
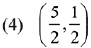
Ans. (3)
Solution.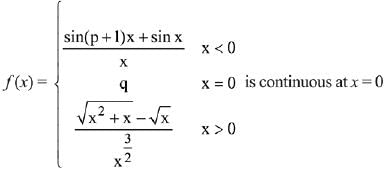
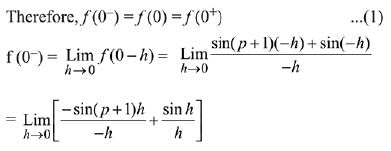
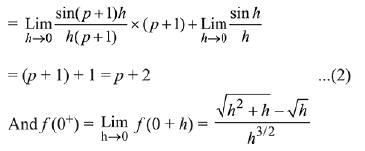
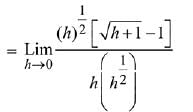
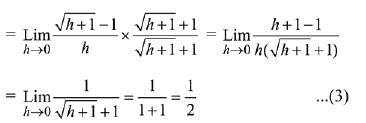
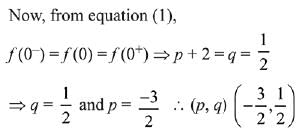
Q.26. Let f : R → R be a continuously differentiable function such that f(2) = 6 and f'(2) = 1/48. (2019)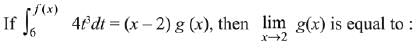
(1) 18
(2) 24
(3) 12
(4) 36
Ans. (1)
Solution.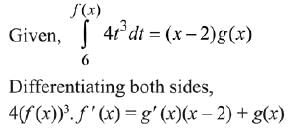
Q.27. 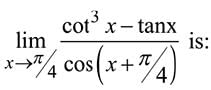 (2019)
(2019)
(1) 4
(2) 4√2
(3) 8√2
(4) 8
Ans. (4)
Solution.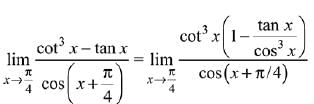
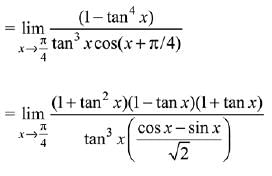
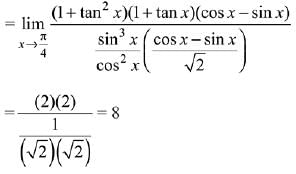
Q.28. 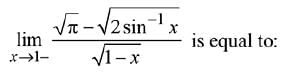 (2019)
(2019)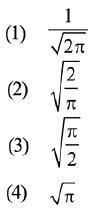
Ans. (2)
Solution.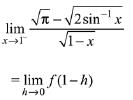
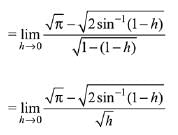
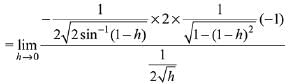
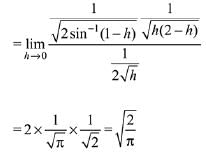
Q.29. If the function f defined on 
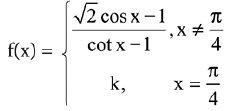
is continuous, then k is equal to: (2019)
(1) 2
(2) 1/2
(3) 1
(4) 1/√2
Ans. (2)
Solution.
Since, f(x) is continuous, then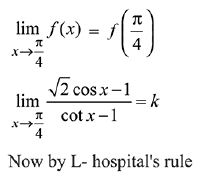
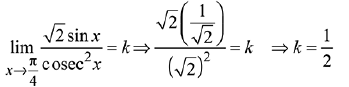
Q.30. Let f(x) = 15 - |x - 10|; x ∈ R. Then the set of all values of x, at which the function, g(x) = f (f(x)) is not differentiable, is: (2019)
(1) {5,10,15}
(2) {10,15}
(3) {5, 10,15,20}
(4) {10}
Ans. (1)
Solution.
Since, f(x)= 15 - |(10-x)|
∴ g(x) = f(f(x)) = 15 - |10 - [15 - |10-x|]|
= 15 — || 10 — x| — 5|
∴ Then, the points where function g(x) is Non-differentiable are
10 - x = 0 and |10 — x| = 5
⇒ x = 10 and x - 10 = ± 5
⇒ x = 10 and x = 15, 5
Q.31. 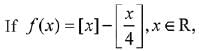 where [x] denotes the greatest
where [x] denotes the greatest
integer function, then: (2019)
(1) f is continuous at x = 4.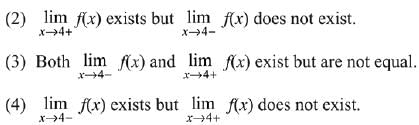
Ans. (1)
Solution.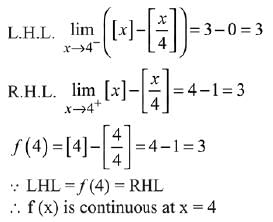
Q.32. If the function 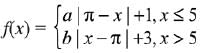 is continuous at x = 5, then the value of a - b is: (2019)
is continuous at x = 5, then the value of a - b is: (2019)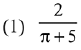
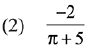
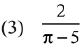
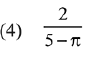
Ans. (4)
Solution.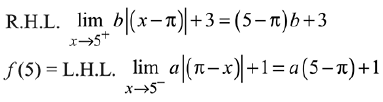
∵ Function is continuous at x = 5
LHL = RHL
(5 - π) b + 3 = (5 - π) a + 1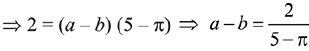
Q.33. 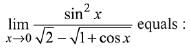 (2019)
(2019)
(1) 4√2
(2) √2
(3) 2√2
(4) 4
Ans. (1)
Solution.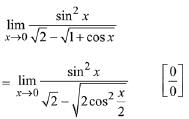
Q.34. Let f : R → R be a differentiable function satisfying f'(3)+f’(2) = 0. Then 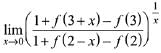 is equal to: (2019)
is equal to: (2019)
(1) 1
(2) e-1
(3) e
(4) e2
Ans. (1)
Solution.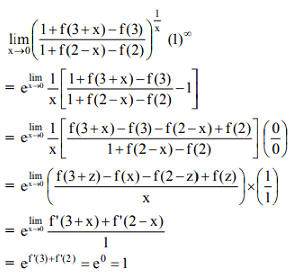
Q.35. If f: R → R is a differentiable function and f(2) = 6, then  (2019)
(2019)
(1) 24f'(2)
(2) 2f'(2)
(3) 0
(4) 12f'(2)
Ans. (4)
Solution.
Using L' Hospital rule and Leibnitz theorem, we get
Putting x = 2,
2f(2)f'(2) = 12f'(2) [∵ f(2) = 6]
Q.36.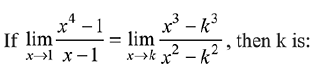 (2019)
(2019)
(1) 8/3
(2) 3/8
(3) 3/2
(4) 4/3
Ans. (1)
Solution.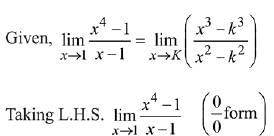
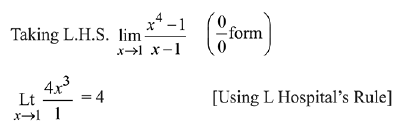
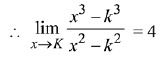
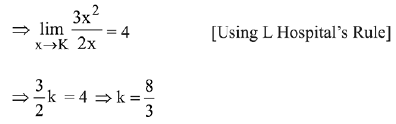
Q.37.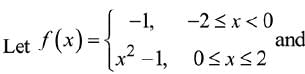
g(x)= |f(x)|+f(|x|). Then, in the interval (-2,2), g is: (2019)
(1) differentiable at all points
(2) not continuous
(3) not differentiable at two points
(4) not differentiable at one point
Ans. (4)
Solution.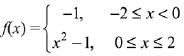
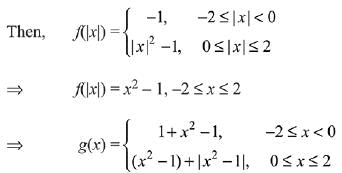
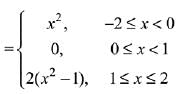
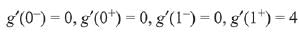
⇒ g(x) is non-differentiable at x = 1
⇒ g(x) is not differentiable at one point.
Q.38. Let K be the set of all real values of x where the function f(x) = sin |x| - |x| + 2 (x - π) cos |x| is not differentiable. Then the set K is equal to: (2019)
(1) φ (an empty set)
(2) {π}
(3) {0}
(4) {0,π}
Ans. (1)
Solution.
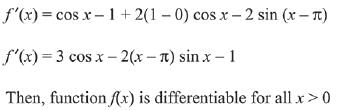
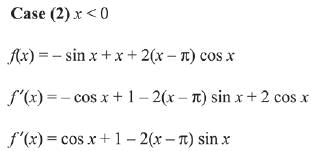
Then, function f(x) is differentiable for all x < 0
Now check for x = 0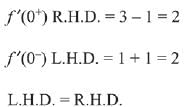
Then, function f(x) is differentiable for x = 0. So it is differentiable everywhere
Hence, k = φ
Q.39. Let S be the set of all points in (- π , π) at which the function f(x) = min {sinx, cosx} is not differentiable. Then S is a subset of which of the following? (2019)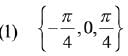
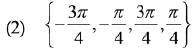
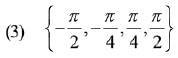
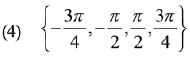
Ans. (2)
Solution.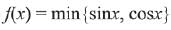
∵ f(x) is not differentiable at 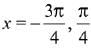
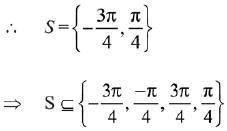
Q.40. Let f: [- 1, 3] → R be defined as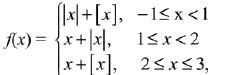
where [t] denotes the greatest integer less than or equal to t. Then, f is discontinuous at: (2019)
(1) only one point
(2) only two points
(3) only three points
(4) four or more points
Ans. (3)
Solution. Given fumction is,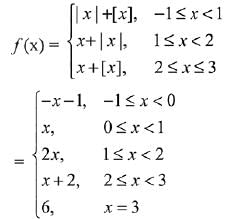
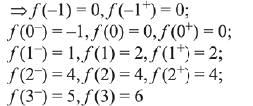
f(x) is discontinuous at x = {0, 1, 3}
Hence, f(x) is discontinuous at only three points.
Q.41. 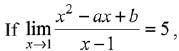 then a + b is equal to: (2019)
then a + b is equal to: (2019)
(1) -4
(2) 5
(3) -7
(4) 1
Ans. (3)
Solution.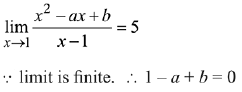

⇒ 2 - a = 5 ⇒ a = - 3 and b = - 4
Then a + b = -3-4 = -7
Q.42.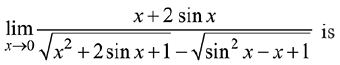 (2019)
(2019)
(1) 6
(2) 2
(3) 3
(4) 1
Ans. (2)
Solution.
Given limit is,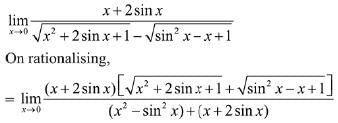
Q.43. Let f(x) = 5-|x - 2| and g(x) = |x+ 1|, x ∈ R. If f(x) attains maximum value at α and g(x) attains minimum value at β, then 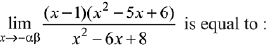 (2019)
(2019)
(1) 1/2
(2) -3/2
(3) -1/2
(4) 3/2
Ans. (1)
Solution.
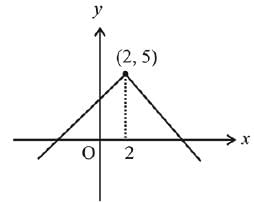
By the graph f(x) is maximum at x = 2
∴ α = 2
g (x) = |x + 1|
Graph of y = g (x)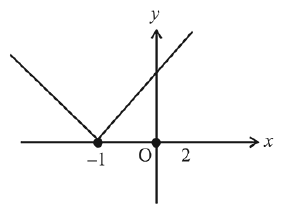
By the graph g (x) is minimum at x = - 1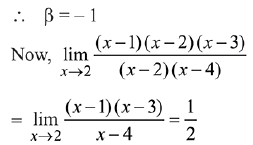
Q.44. Let f: (- 1, 1) → R be a function defined by f(x) = max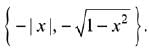 If K be the set of all points at which f is not differentiable, then K has exactly: (2019)
If K be the set of all points at which f is not differentiable, then K has exactly: (2019)
(1) five elements
(2) one element
(3) three elements
(4) two elements
Ans. (3)
Solution. Consider the function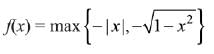
Now, the graph of the function
From the graph, it is clear that f(x) is not differentiable at 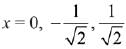
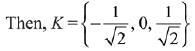
Hence, K has exactly three elements.
Q.45. For each t ∈ R, let [t] be the greatest integer less than or equal to t. Than 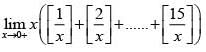 (2018)
(2018)
(1) is equal to 0
(2) is equal to 50
(3) is equal to 120
(4) does not exist (in R)
Ans. (3)
Solution.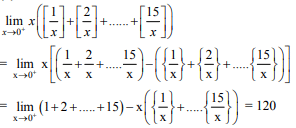
Q.46. Let S = {t ∈ R:f(x)= |x - π|.(e|x| - 1) sin |x| is not differentiable at t}. Then the set S is equal to: (2018)
(1) ϕ (an empty set)
(2) {0}
(3) {π}
(4) {0,π}
Ans. (1)
Solution.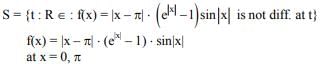
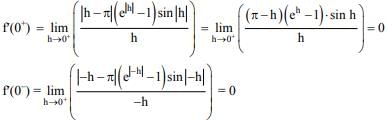
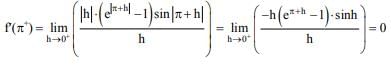

Q.47. Let S = {λ, µ) ∈ R × R : f(t) = (|λ|e|t| − µ).sin (2|t|), t ∈R, is a differentiable function}. Then S is a subset of∶ (2018)
(1) R × [0, ∞)
(2) R × (-∞, 0)
(3) (-∞, 0) × R
(4) [-∞, 0) × R
Ans: (1)
Solution:
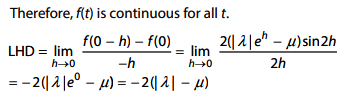
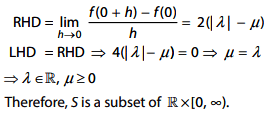
Q.48. If f(x) = 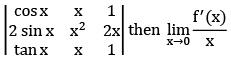 (2018)
(2018)
(1) Exists and is equal to -2
(2) Exists and is equal to 0
(3) Does not exist
(4) Exists and is equal to 2
Ans: (1)
Solution: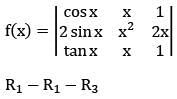
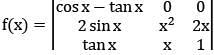
= cos x − tan x [x2 − 2x2]
= x2 tan x − x2 cos x
f′(x) = 2x tan x + x2 sec2 x − 2x cos x + x2 sin x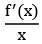 = 2 tan x + x sec2 x − 2 cos x + x sin x
= 2 tan x + x sec2 x − 2 cos x + x sin x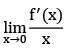 = 0 + 0 − 2 + 0 = −2
= 0 + 0 − 2 + 0 = −2
Q.49.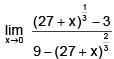 equals: (2018)
equals: (2018)
(1) -1/6
(2) 1/6
(3) 1/3
(4) -1/3
Ans: (1)
Solution: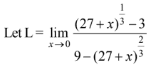
Here ‘L’ is in the indeterminate i.e., 0/0
∴ using the L’ Hospital rule we get: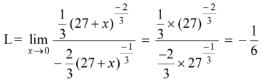
Q.50. If the function f defined as f(x) = 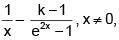 is continuous at x = 0, then the ordered pair (k, f(0)) is equal to: (2018)
is continuous at x = 0, then the ordered pair (k, f(0)) is equal to: (2018)
(1) (2, 1)
(2) (3, 1)
(3) (3, 2)
(4)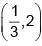
Ans: (2)
Solution:
If the function is continuous at x = 0, then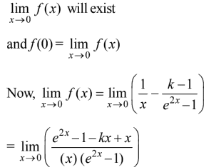
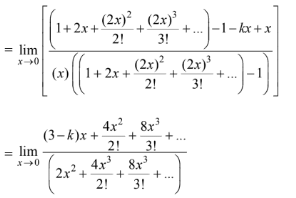
For the limit to exist, power of x in the numerator should be greater than or equal to the power of x in the denominator. Therefore, coefficient of x in numerator is equal to zero
⇒ 3 - k = 0
⇒ k = 3
So the limit reduces to
Q.51. 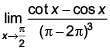 equals (2017)
equals (2017)
(1) 1/4
(2) 1/24
(3) 1/16
(4) 1/8
Ans. (3)
Solution.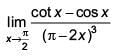
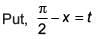
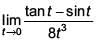
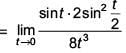
= 1/16.
Q.52. 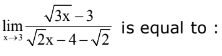 (2017)
(2017)
(1) 1/√2
(2) 1/2√2
(3) √3/2
(4) √3
Ans. (1)
Solution.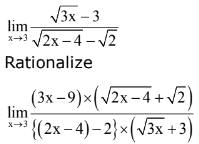
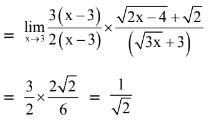
Q.53. The value of K for which the function is continuous at x = π/2, is (2017)
(1) 2/5
(2)
(3) 17/20
(4) 3/5
Ans. (4)
Solution.
k + 2/5 = 1
k = 1 - 2/5 = 3/5
Q.54. for some positive real number a, then a is equal to (2017)
(1) 17/2
(2) 15/2
(3) 7
(4) 8
Ans. (3)
Solution.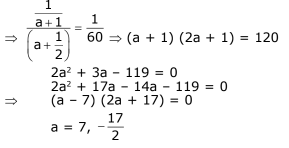
Q.55. Let p = 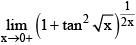 then loge p is equal to: (2016)
then loge p is equal to: (2016)
(1) 2
(2) 1
(3) 1/2
(4) 1/4
Ans. (3)
Solution: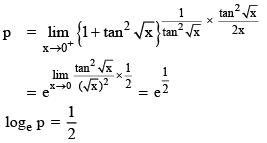
Q.56. For x ∈ R, f(x) = |log 2 - sin x| and g(x) = f(f(x)), then: (2016)
(1) g is not differentiable at x = 0
(2) g'(0) = cos (log 2)
(3) g'(0) = - cos(log 2)
(4) g is differentiable at x = 0 and g'(0) = -sin(log 2)
Ans. (2)
Solution: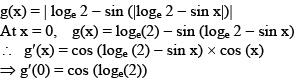
Q.57. is equal to: (2016)
is equal to: (2016)
(1)
(2)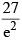
(3)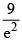
(4) 3 log 3 - 2
Ans. (2)
Solution.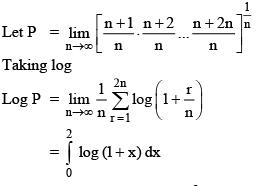
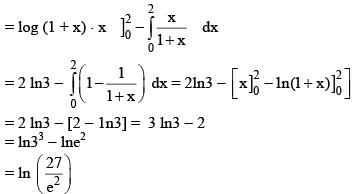
P = 27/e2
Q.58. If f(x) is a differentiable function in the interval (0, ∞) such that f(1) = 1 and for each x > 0, then f(3/2) is equal to: (2016)
(1) 13/6
(2) 23/18
(3) 25/9
(4) 31/18
Ans. (4)
Solution.
Differentiate w.r.t. t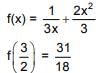
Q.59. 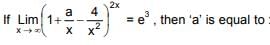 (2016)
(2016)
(1) 2/3
(2) 3/2
(3) 2
(4) 1/2
Ans. (2)
Solution.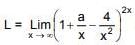 must be of the from 1∞
must be of the from 1∞
⇒
= e2a = e3
a = 3/2
Q.60. Let a,b ∈ R, (a ≠ 0). If the function f defined as (2016)
Ans. (1)
Solution.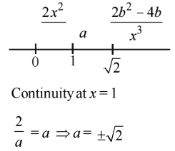
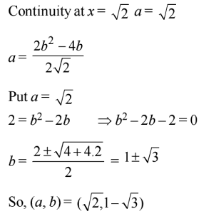
Q.61.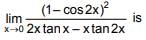 (2016)
(2016)
(1) 2
(3) 1/2
(4) -2
Ans. (4)
Solution.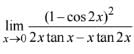




|
152 videos|196 docs|201 tests
|





















