Jacobian, Complex Analysis | Basic Physics for IIT JAM PDF Download
Although we will not prove it, the general result for a change of coordinates in an n-dimensional integral from a set xi to a set yj (where i and j both run from 1 to n) is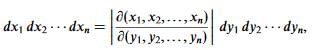
where then-dimensional Jacobian can be written as an n×n determinant in an analogous way to the two- and three-dimensional cases.
For readers who already have sufficient familiarity with matrices and their properties, a fairly compact proof of some useful general properties of Jacobians can be given as follows. Other readers should turn straight to the results (6.16) and (6.17) and return to the proof at some later time.
Consider three sets of variables xi,yi and zi, with i running from 1 to n for each set. From the chain rule in partial differentiation , we know that 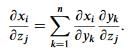 (6.13)
(6.13)
Now let A,B and C be the matrices whose ijth elements are∂xi/∂yj,∂yi/∂zj and∂xi/∂zj respectively. We can then write (6.13) as the matrix product 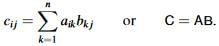 (6.14)
(6.14)
We may now use the general result for the determinant of the product of two matrices, namely |AB|=|A||B|, and recall that the Jacobian 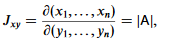 (6.15)
(6.15)
and similarly for Jyz and Jxz. On taking the determinant of (6.14), we therefore obtain
Jxz=Jxy Jyz
or, in the usual notation,
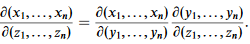 (6.16)
(6.16)
As a special case, if the set zi is taken to be identical to the set xi,and the obvious result Jxx= 1 is used, we obtain
Jxy Jyx=1
or, in the usual notation,
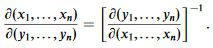 (6.17)
(6.17)
The similarity between the properties of Jacobians and those of derivatives is apparent, and to some extent is suggested by the notation. We further note from(6.15) that since|A|=|AT|,where AT is the transpose of A, we can interchange the rows and columns in the determinantal form of the Jacobian without changing its value.
|
210 videos|156 docs|94 tests
|
FAQs on Jacobian, Complex Analysis - Basic Physics for IIT JAM
| 1. What is the Jacobian matrix and how is it used in mathematics? |  |
| 2. How does complex analysis contribute to physics? |  |
| 3. What are some applications of complex analysis in physics? |  |
| 4. What are the key concepts in complex analysis relevant to physics? |  |
| 5. How does complex analysis relate to the study of quantum mechanics? |  |

|
Explore Courses for Physics exam
|

|

















