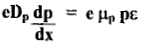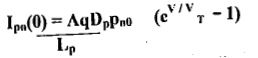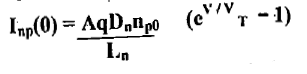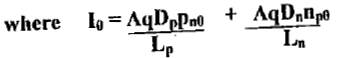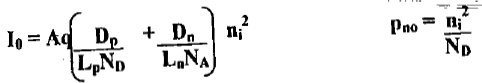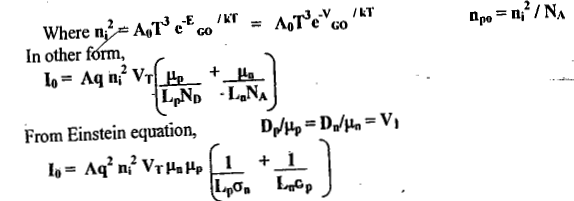Junction Theory & Different Types of Diodes & Their Characteristics - 1 | Electronic Devices - Electronics and Communication Engineering (ECE) PDF Download
Semiconductor Diode Characteristic
The p- and n-type silicon or germanium can be obtained by adding appropriate acceptor or donor impurity into Si or Ge-mell while growing a crystal.
These crystals arc cut into thin slices called ‘Wafers’. Semiconductor devices are usually made on these wafers.
These aremany methods of making a p-n junction as given below.
(a) ‘Alloying’ technique
(b) Diffusion technique
(c) Vapour deposition (epitaxial growth) and
(d) Rate growth junction.The donor ion is indicated schematically by a plus sign ( + ) because, after this impurity atom “donates” ah electron it becomes a positive ion. The acceptor ion is indicated by a minus sign
(-) because, after this atom “accepts” an electron, it becomes a negative ion.
Initially, there are nominally only p-type carriers to the left of the junction and only n-lypc carriers to the right.
Because, there is a density gradient across the junction holes will diffuse to the right across the junction and electrons to the left.
Asa result of the displacement of these carriers, an electric field will appear across the junction. Equilibrium will be established when the field becomes large enough to restrain the process of diffusion.
The un neutralized ions in the neighborhood of the junction are referred to as “uncovered charges”. Since the region of the junction is depleted of mobile charges, it is called the “depletion region, the space-charge region, or the transition region”.
The thickness of this region is of the order of 10-4 cm = 10-6 m = 1 micron
The general shape of the charge distribution may be as shown in figure 1.1b.
The electric field intensity in the neighborhood of the junction is indicated in fig 1.1c.
The electrostatic-potential variation in the depletion region is shown in fig l.ld.
This variation constitutes a potential energy barrier against the further diffusion of holes across the barrier.
The form of the potential energy barrier against the flow of electrons from the n-side across the junction as shown in fig l.le.
The potential bamer (or field across the junction) and the depletion layer width (or junction width) depends upon the doping concentration on the two sides.
At equilibrium, there is no net current flowing across the p-n junction.
The current due to the drift of carriers in the electric field must exactly cancel the diffusion current. Jp(drift) + Jp(diffusion) - 0
Jn(drift) + Jn(diffusion) - 0Since the net hole current density is zero, the negative of the hole diffusion current must equal the hole drift current.

The potential barrier V0 called the contact, or diffusion, potential is of the order of magnitude of a few tenths of a volt.V2V = d2V/dx2 = - ρ/ε → Poisson equation is satisfied inside the junction.
V2V = d2V/dx2 = 0 → Laplace equation is satisfied outside the junction.
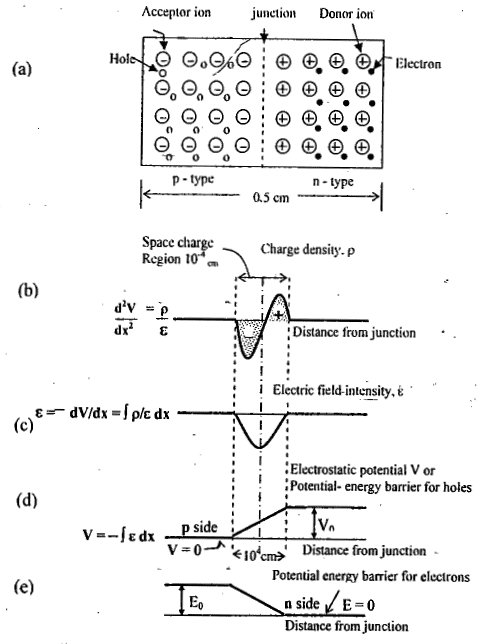 A schematic diagram of a p - n junction, including the charge density, electric field intensity, and potential - energy barriers at the junctions, (not drawn to scale.)
A schematic diagram of a p - n junction, including the charge density, electric field intensity, and potential - energy barriers at the junctions, (not drawn to scale.)
The P-N Junction as a Diode
Diode permits the easy flow of current in one direction but restrains the flow in die opposite direction.
Forward Bias:
Suppose we apply a voltage V such that n-side is negative and p-side is positive.
The applied voltage V (or bias V) is opposite to the junction barrier potential V
The consequences of this are:
(i) The effective barrier potential becomes (Vo — V) and hence the energy barrier across the junction decreases.
(ii) more majority carriers will be allowed to flow across the junction.
(iii) the junction width decreases.The current flow is principally due to majority charge carriers and is large (mA).
Reverse Bias:
The applied voltage V on the n-side is positive and is negative on the p-side.
The applied bias V and the barrier potential V# are in the same direction making the effective junction potential as V + Vo. As a result, the junction width will increase.
The higher junction potential would restrict the flow of majority carriers to a much greater extent.
However, such a field will favour the flow of minority carriers (as they have opposite charges).
So, the reverse bias current will be due to the minority carriers only.
Since, the number of minority carriers is very small as compared to the majority carriers, the reverse bias current is small (≈ μA).
The short circuited and Open circuited P-N Junction
- If the voltage V applied to the p-n junction is set equal to zero, the p-n junction would beshort-circuited.
- Under this condition, no current can flow (I = 0) and the electrostatic potential Vo remains uncharged and equal to the value under open circuit conditions.
- The sum of the voltages around the closed loop must be zero, the junction potential V0 must be exactly compensated by the metal to semiconductor contact potentials at the ohmic contacts.
- It is not possible to measure contact difference of potential directly with a voltmeter across an open-circuited p-n junction diode and the voltmeter would read zero voltage.
Band AND Structure Of An Open-Circuited PN Junction
- The Fermi level must be constant throughout the specimen at equilibrium.
- The Fermi level EF is closer to the conduction band edge Ecn in the n-type material and closer to the valence band edge Evp in the p-side.
- The conduction band edge Ecp in the p material cannot be at the same level as Ecn, nor can the valence band edge Evn in the n-side line up with Evp. Hence the energy bandagram for a p-n junction appears as shown in fig.2 Where a shift in energy levels E0 is indicated. Note that
E0 = Ecp - Ecn = Evp - Evn = E1 + E2
This energy E0 represents the potential energy of the electrons at junction.
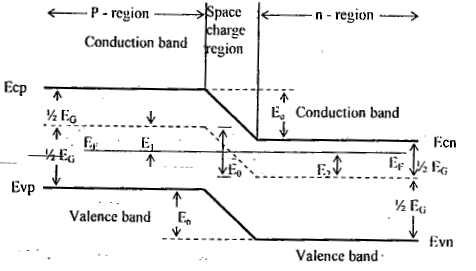 Band diagram for a p-n junction under open-circuit conditions. This sketch corresponds to fig (le) and represents potential energy for electrons. The width of the forbidden gap is Eg in electron volts.From figure,
Band diagram for a p-n junction under open-circuit conditions. This sketch corresponds to fig (le) and represents potential energy for electrons. The width of the forbidden gap is Eg in electron volts.From figure,
EF - Evp - 1/2 EG - E1 and ECn - EF - 1/2 EG - E2 EG = forbidden energy gap
By adding the above equations
E0 = E1 + E2 = EG - (ECn - EF) - (EF - EVp)
EG = kT In |(NCNv) / ni2] ....(1)
Ecn - EF = kT ln (NC/ND) ....(2) ∴ KT = 26 meV
EF - Evp = kT ln (Nv/NA) ....(3)
The E’s are expressed in electron volts and-k has the dimensions of electron volts per degree Kelvin. The Contact difference in potential V0 is expressed in volts and is numerically equal to E0 and it is depends only upon the equilibrium concentrations, and not at all upon the charge density in the transition region(space charge region).
Other expressions for E0 are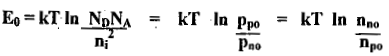 ....(4)
....(4)
Rewriting the above equation (4) in another form
pp0 = pn0 ev0/vT
nn0 = np0 ev0/vT ....(5)
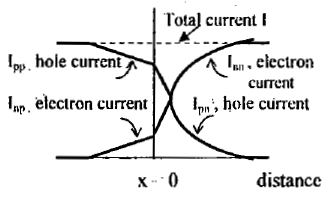
The hole and electron-current components vs, distance in a p-n junction diode. The space-charge region at the junction is assumed to be negligibly email
The Current Components in p-n Diode
- When a forward bias is applied to a diode, holes are injected into the n-side and electrons into the p-side.
- The number of these injected minority carriers falls off exponentially with distance from the junction as shown in fig.(3)
- The symbol Ipn(x) represents the hole current in the n material, and Inp(x) indicates the electron current in the p-side as a function of x.
- Electrons crossing the junction at x = 0 from right to left constitute a current in the same direction as holes crossing the junction from left to right. Hence the total current I at x = 0 is
I = Ipn(0) + Inp(0)
- Consequently, in the p-side, there must be a second component of current Ipp which, when added to Iup, gives.the total current I. Hence this hole current in the p-side Ipp(a majority carrier current) is given by
Ipp(x) = I - Inp(x)
- This current is plotted as a function of distance as shown in fig.(3) as is also the corresponding electron current lnn in the n material.
- For an un symmetrically doped diode, Ipn ≠ Inp.
- The current in a p-n diode is bipolar in character since it is made up of both positive and negative carriers of electricity.
- The total current is constant throughout the device, but the proportion due to holes and that due to electrons varies with distance.
Quantitative Theory of the P-N diode Currents
If the forward bias is applied to the diode, holes are injected from the p side into the n material. The concentration pn of holes in the n-side is increased above its thermal equilibrium value pno and, is given byPn(x) = Pno + Pn(0)e-x/Lp ....(6)
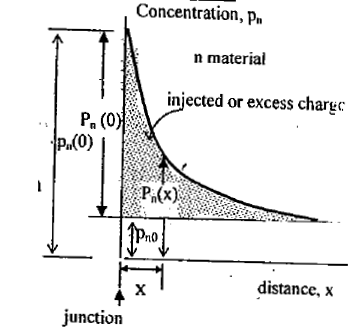
Defining the several components of hole concentration in the n side of a forward - biased diode.
Where the parameter Lp is called the diffusion length for holes in the n material.
And the injected or excess concentration at x = 0 is
Pn(0) = Pn(0) - Pno
The diffusion hole current in the n-side is given by
junction
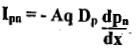 ....(7)
....(7)
Taking the derivative of equation (6) and substituting in equation (7) we obtain
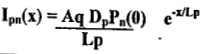 .... (8)
.... (8)
This equation verifies that the hole current decreases exponentially with distance.
Where q = charge of an electron
The Law of the Junction
- If the barrier potential across the depletion layer is VB, then
Pp = PnevB/VT ....(9)
This is the Boltzmann relationship of kinetic gas theory. - If we apply above equation to the case of an open-circuited p-n junction, then
Pp = Ppo, Pn = Pn0 and VB = V0. - Consider now a junction biased in the forward direction by an applied voltage V.
- Then the barrier voltage VB is decreased from its equilibrium value V0 by the amount or
Vb = V0 - V
V0 = equilibrium value - At the edge of the depletion layer, x = 0, pn = pn(0), then the above equation(9) is
Pp0 = Pn(0)e(V0 -V/Vt] ....(10)
Combining this equation with the above said equation(5), i.e., pp0 = pn0 eV0/VT
We obtain,
Pn(0) = Pn0ev/vT ....(11) - This boundary condition is called the “law of the junction”. It indicates that, for a forward bias (V > 0), the hole concentration pn(0) at the junction is greater than the thermal - equilibrium value pn0.
- A similar equation, valid for electrons, is obtained by interchanging p and n itt above equation( II).
- The hole concentration Pn(0) injected into the n side at the junction is given by
Pn(0) = Pn0(eV/VT-1) ....(12)
The Forward Currents
- The hole current Ipn(0) crossing the junction into the n-side at x = 0 is given by

- The electron current Inp(0) crossing the junction into the p-side is obtained from above equation by interchanging n and p, or

The total diode current I is the sum of Ipn(0) and Inp(0), or
I = I0(CV/VT -1)
Hence I0 is called the "‘reverse saturation current!’ and depends on doping concentration.

Where, σn = NDμnq and σp = NAμpq
VGO is a voltage which is numerically equal to the forbidden gap energy in electron volts. If we consider the recombination of carriers, then the total current I
I = I0(ev/n VT -1) ....(13)
Where η ≈ 2 for small (rated) currents and η ≈ 1 for large currents.
η ≅ 2 for silicon
η ≅ 1 for germanium - I0 depends on material and it is fixed for a given device. But varies with temperature
Io2 = I01 x 2I(T2 - T1)10l ....(14) - Where Io1 (I02) is the reverse saturation current at a temperature T1 (T2).
- I0 doubles for every 10°C rise in temperature. That is, it increases 7% / °C.
- I0 is in the range of microamperes for a germanium diode andTVano amperes for a silicon diode.
- Since n = 2 for small currents in silicon, the current increases as ev/2vT for the first several tenths of a volt and increases as ev/vT only at higher voltages.
The Volt-Ampere Characteristic
For a p-n junction, the current I is related to the voltage V by the equation
I = I0(ev/ηvT -1) ....(13)
η ≅ 1 for Ge
η ≅ 2 for Si
VT = T/11,600 = 26 m V at T = 300°K.
At room temperature,
(a) When the voltage V is positive and several times VT , the unity in the parenthesis of equation (13) may be neglected, i.e., ev/ηvT >>1,
∴ l = l0 ev/ηv T
Accordingly except for a small range in the neighborhood of the origin, the current increases exponentially with voltage.
(b) When the diode is reverse-biased and |V| is several times VT, I ≈ - I0. The “reverse
current” is therefore constant, independent of the applied reverse bias. Consequently, I0 is referred to as the “reverse saturation current”
At a reverse biasing voltage Vz, the diode characteristic exhibits an abrupt and marked departure from (13). At this critical voltage a large reverse current flows, and the diode is said to be in the “break down region”.
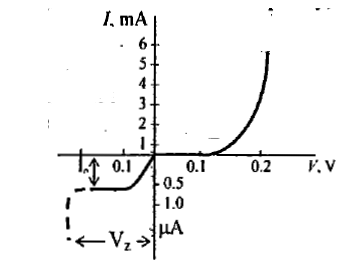 The volt-ampere characteristic for a germanium diode
The volt-ampere characteristic for a germanium diode
The Cutin Voltage, Offset, break-point, or threshold voltage (Vy):
Below Vy the current is very small (say, less than 1 per cent of max. rated voltage).
Beyond Vy the current rises very rapidly. Vy = 0.2 V for Ge, 0.6V for Si.
The reverse saturation current 10 in a Ge is normally larger by a factor of about 1000 than the 10 in a silicon diode of comparable ratings. Since n = 2 for small currents in Si, the 1 increases as eV/2VT only at higher voltages.
The resistance R, cutin voltage Vy, power dissipation and noise margin of Germanium is less— than the silicon. But Germanium is not used in switching characteristics.
The temperature dependence of p-n diode characteristics:
The dependence of 10 on temperature T is given approximately by
I0 = kTm e-v Go/ηvT
Where k is constant and qVGO (q is the magnitude of the electron charge) is the forbidden gap energy in Joules:
For Ge : n = 1 m = 2 VGO = 0.785V
For Si: n = 2 m = 1.5 VGO = 1.21V
Taking the derivative of the logarithm of above equation, we find
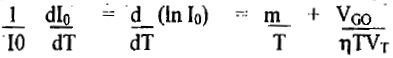
At room temperature, d(lnl0)/dT = 0.08 /°C for Silicon and 0.11 / °C for Germanium.
The 10 increases approximately 7 percent / °C for both Si and Ge. Since (1.07)10 ≈ 2.0, we conclude that the “reverse saturation current(Io)” approximately doubles for every 10°C rise in temperature.
Consider a diode operating at room temperature (300°K) and just beyond the Vy.
Then we find,
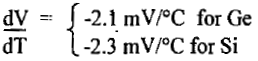
Since these data are based on “average characteristics”, it might be well for conservative design to assume a value of
dV / dT = -2.5 mV/°C ....(14)
for either Ge or Si at room temperature.
For Germanium, an increase in temperature from room temperature (25°C) to 90°C increases the 10 to hundreds of microamperes, although in Silicon at 100°C the 10 has increased only to some tenths of a micro ampere.
|
21 docs|29 tests
|
FAQs on Junction Theory & Different Types of Diodes & Their Characteristics - 1 - Electronic Devices - Electronics and Communication Engineering (ECE)
| 1. What is junction theory in electronics? |  |
| 2. What are diodes and what are their characteristics? |  |
| 3. What are the different types of diodes? |  |
| 4. How does a diode work? |  |
| 5. What are the applications of diodes? |  |