Kepler's Laws of Planetary Motion | Science Class 9 PDF Download
Kepler's Laws of Planetary Motion
Johannes Kepler was a 16th century astronomer who established three laws which govern the motion of planets (around the sun). These are known as Kepler's laws of planetary motion. The same laws also describe the motion of satellites (like the moon) around the planets (like the earth). The Keplar's laws of planetary motion are given below.
Kepler's First Law
The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit.
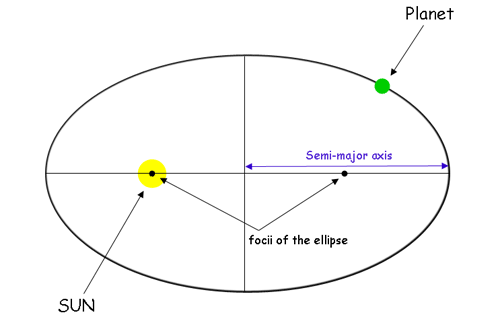
Kepler's Second Law
Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time.
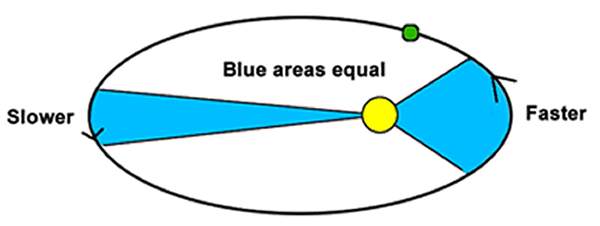
Kepler's Third Law
The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun.The law can be expressed as :
r3 ∝ T2
or r3 = constant × T2
where r = Mean distance of planet from the sun
and T = Time period of the planet (around the sun)
Through Kepler gave the laws of planetary motion but he could not give a theory to explain the motion of planets. It was Newton who showed that the cause of the motion of planets is the gravitational force which the sun exerts on them. In fact, Newton used the Kepler's third law of planetary motion to develop the law of universal gravitation.
Newton's Inverse-square Rule
The force between two bodies is inversely proportional to the square of distance between them' is called the inverse-square rule.
Consider a planet of mass m moving with a velocity (or speed) v around the sun in a circular orbit of radius r, A centripetal force F acts on the orbiting planet (due to the sun) which is given by :
The mass m of a given planet is constant
If the planet takes time T to complete one revolution (of 2pr) around the sun, then its velocity v is given by:
The factor 2π is a constant
Now, taking square on both sides
If we multiply as well as divide the right side of this relation by r
The factor is constant by Kepler's third law.
by putting 1/r in place of v2 in relation
or
Newton's Third Law of Motion and Gravitation
Newton's third law of motion also holds good for the force of gravitation. This means that when earth exerts a force of attraction on an object, then the object also exerts an equal force on the earth, in the opposite direction.
According to Newton's second law,
Force = Mass × Acceleration
F = ma
Acceleration
The mass of earth is very very large and acceleration produced in the earth very very small and cannot be detected with even the most accurate instrument available to us.
Free Fall
Any object dropped from some height always falls towards the earth. If a feather and a stone are dropped from the top of a tower, it is observed that feather falls onto the ground much later than the stone. So, it was thought that object of different masses dropped from same height take different times to reach the ground
However, Galileo dropped three iron balls of different masses simultaneously from the top of the tower of Pisa and found that all the three balls reached the earth's surface at the same time.
Galileo explained that the feather suffered much air resistance during fall because of its large surface area. Due to this opposing force, feather takes longer time to reach the ground than the stone. He further explained that if air resistance is eliminated, both feather and the stone will reach the ground simultaneously.
Conclusion: Galileo concluded that the bodies of different masses dropped simultaneously from the same height hit the ground at the same time, if air resistance is neglected.
Definition of Free Fall
The falling body on which only force of gravitaion of the earth acts is known as freely falling body and such fall of a body is known as free fall. A freely falling body has acceleration equal to acceleration due to graveily(g).
Experimental Verification
This fact was verified experimentally by Robert Boyle just after the death of Galileo. Robert Boyle used his newly invented vacuum pump to evacuate the air from a long jar containing a lead bullet and a feather. Then he inverred the jar and found that both the bullet and the reached the bottom of the jar at the same time.
If the air resistance is neglected or not taken into account, then the only force acting on the falling body is the force of gravitation of the earth. This force of gravitation of the earth is constant and hence produces a constant acceleration in the body. Since this acceleration is produced by the gravitational force of the earth and hence known as acceleration due to gravitational force of earth or acceleration due to gravity.
Acceleration due to Gravity
The acceleration with which a body falls towards the earth due to earth's gravitational pull is known as acceleration due to gravity. It is denoted by 'g'.
Thus, all bodies irrespective of their masses fall down with constant acceleration.
To Calculate the Value of g
When a body of mass m is dropped from a certain distance R from the centre of earth of mass M, then the force exerted by the earth on the body is
Let this force produces an acceleration a in mass m.
∴ F = ma or F = mg ... (ii)
From (i) and (ii),
For bodies falling near the surface of earth, this acceleration is called acceleration due to gravity and is represented by g.
where M is the mass of the earth i.e., 6 × 1024 kg and R, the radius of the earth i.e., 6.4 × 106 m
Value of g on Moon
Mass of moon = 7.4 × 1022 kg and its radius = 1,740 km
or R = 1,740,000 m = 1.74 × 106 m
Mass of the Earth
We can determine mass of the earth from equation (A)
∴
Average Density of the Earth
It can also be determined from equation (A) above.
Calculation of acceleration due to gravity on the moon and to prove that it is 1/6th of the acceleration due to gravity on the earth.
Mass of the moon (M) = 7.4 × 1022 kg
Radius of the moon (R) = 1.74 × 106 m
Gravitational constant (G) = 6.7 × 10-11 Nm2/kg2
Acceleration due to gravity on the moon,
High Order Thinking Skill
Variation in the value of 'g'
1. Variation in the value of 'g' with the shape of the earth.
The acceleration due to gravity 'g' on the surface of the earth is given by
This expression for 'g' is calculated by considering the earth as a spherical body.
In fact, the earth is not sphereical in shape but it is egg shaped as shown in figure.
Therefore, the radius of the earth (R) is not constant throughout. Hence, the value of 'g' is different at different points on the earth.
The equatorial radius (RE) of the earth is about 21 km longer than its polar radius RP).
Now from equation (1), value of 'g' at equator is given by
Value of 'g' at pole is given by
Dividing equation (3) by equation (2), we get
Since RE > RP ∴ gP > gE
Thus, value of 'g' is more at equator than at poles
2. Variation in the value of 'g' with the altitude (or height) above the surface of the earth.
We know, acceleration due to gravity on the surface of the earth. The distance of the body from the centre of the earth = (R h).
Therefore, acceleration due to gravity at height 'h' is given by
Dividing (2) by (1), we get
Since (R + h) > R
This shows that the value of 'g' decreases as we go higher and higher.
Thus, value of 'g' decreases with the height from the surface of the earth.
3. Variation in the value of 'g' with depth below the surface of the earth
The value of 'g' decreases with depth below the surface of the earth.
The value of 'g' at depth d below the surface of the earth is given by
division (2) by (1)
At the centre of the earth d = R g' = g0
Do You Know?
1. The acceleration due to gravity of a planet depends on its mass and its radius. Its value is high if mass is large and radius is small.
2. The value of g at the surface of earth is 9.8 ms-2 on an average.
3. The value of g decreases with height.
4. The value of g decreases with depth.
5. The value of g is more at poles and less at equator.
6. The value of g is zero at the centre of the earth.
7. The value of acceleration due to gravity is minimum at planet mercury and maximum at planet jupiter.
8. Acceleration due to gravity is independent of mass shape size etc of falling body i.e. there will be equal acceleration in a light and heavy falling body.
9. The rate of decrease of the acceleration due to gravity with height is twice as compared to that with depth.
10. If the rate of rotation of earth increases the value of acceleration due to gravity decreases at all places on the surface of the earth except at of poles.
11. If earth stops rotating there will be increase in the value of acceleration due to gravity at equator by a value =RW2 = 0.034 m/s2 but there will be no change in the value of g at poles.
Difference between "G" and "g"
| Sr. No. | Acceleration due to gravity (g) | Universal gravitational constant (G) |
| 1 | The acceleration produced in a body falling freely under the action of gravitational pull of the earth is known as acceleration due to gravity | The gravitational force between two bodies of unit masses separated by a unit distance is known as universal gravitational constant. |
| 2 | The value of 'g' is different at different points on the earth. | The value of 'G' is same at every point on the earth. |
| 3 | The value of 'g' decreases as we go higher from the surface of the earth or as we go deep into the earth. | The value of 'G' does not change with height and depth from the surface of the earth. |
| 4 | The value of 'g' at the centre of the earth is | The value of 'G' is not zero at the centre of the earth or anywhere else. |
| 5 | The value of 'g' is different on the surfaces of different heavenly bodies like the sun, the moon, the planets. | The value of 'G' is same throughout the universe. |
| 6 | The value of 'g' on the surface of the earth is 9-8 ms–2. | The value of G = 6.673 × 10–11 Nm2 kg–2 , throughout the universe. |
Motion of Objects under the influence of Gravitational Force of the Earth
When the bodies are falling under influence of gravity, they experience acceleration g i.e., 9.8 ms-2. However, when these are going up against gravity, they move with retardation of 9.8 ms-2. All the equations of motion already read by us are valid for freely falling body with the difference that a is replaced by g. For motions vertically upwards (a) is replased by (-g).
The equation of motion
v = u + at
Replace a = g
v = a + gt when body falls in downward
v = a - gt when body through upward
s = ut + (1/2) at2
Replace a = g & s = h
h = ut +(1/2) gt2
v2 - u2 = 2as
Replace s = h
v2 - u2 = 2gh
|
84 videos|478 docs|60 tests
|
FAQs on Kepler's Laws of Planetary Motion - Science Class 9
| 1. What are Kepler's Laws of Planetary Motion? |  |
| 2. What is Free Fall? |  |
| 3. What is a High Order Thinking Skill? |  |
| 4. What is the difference between "G" and "g"? |  |
| 5. What is the motion of objects under the influence of the gravitational force of the Earth? |  |






















