Kinematic Equations of Motion - Class 11 - CBSE/Schools PDF Download
Ref: https://edurev.in/question/682752/Needed-a-Document-for-kinematics-equations-for-uniformly-accelerated-motion-Related-Motion-Motion-in
Uniform Acceleration
A body under constant acceleration is uniformly accelerated motion. This is when a constant external force is applied to the body. The direction of acceleration is very important in the change of velocity. However, the direction of acceleration of a body may not be same as the direction of its motion. For example, if a car travels at a speed of 60 km/hour then it will cover a distance of 1 km/minute. Here the motion of car acceleration is uniform.
Kinematic Equations of Motion
If an object starts with velocity ”u” and after some time “t” its velocity changes to v, if the uniform acceleration is a and distance traveled in time (t) is s, then we obtain the following kinematic equations of uniformly accelerated motion.
First Equation Of Motion
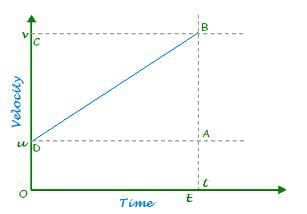
Let an object is moving with uniform acceleration
u = initial velocity of the object
v = final velocity of object
a = uniform acceleration
Let object reach point B after time (t) Now, from the graph
Slope= Acceleration(a)= changeinvelocitytime
Change in velocity = AB= v⃗ −u⃗
Time = AD = t
a = v⃗ −u⃗ t
Solving this we get the first equation of motion:
v⃗ =u⃗ +a⃗ t
Learn more about Relative Velocity Motion in Two Dimensions here.
Second Equation Of Motion
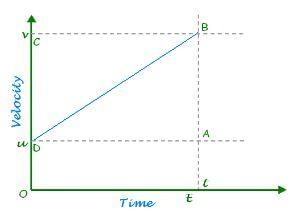
Consider an object starting with an initial velocity u and moving with uniform acceleration a. Distance covered by the object at the given time t is given by the area of the trapezium ABDOE. Let in the given time ‘t’, the displacement covered by the moving object ‘s’ is given by the area of trapezium, ABDOE
Displacement (s) = Area of ABD + Area of ADOE
12 × AB× AD+ AE ×OE, AB= dc= at
= 12 at× t+ ut
Hence, the second equation of motion is:
s⃗ =u⃗ t+12a⃗ t²
Velocity time graph of a uniformly accelerated motion
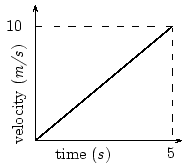
The velocity-time graph of a uniformly accelerated motion is a straight line graph inclining towards the time axis. If the object has positive constant acceleration, the graph slopes upward. In case the object has negative constant acceleration, the velocity-time graph will slope downward.
Learn more about Instantaneous Velocity and Speed here.
Solved Examples For You
Q. An automobile traveling with a speed of 60 Km/h can apply brake to stop within a distance of 20 m If the car is going twice as fast i.e., 120 Km/h the stopping distance will be
- 60m
- 40m
- 20m
- 80m
Answer: D
Q2. A cart that is free to move in one dimension is moving in the positive direction and slowing down under the influence of a constant backward pull until the cart comes to a momentary stop and reverses direction. What are the signs of the cart’s velocity and acceleration during the moment it is stopped?
- velocity : 0 acceleration : +
- acceleration : 0 velocity : +
- velocity : 0 acceleration : –
Answer: C. Since the cart has stopped at the moment, the speed and velocity of the cart are zero.Hence the cart achieves negative velocity which means that it should be accelerating in the negative direction to raise velocity from zero to finite value in the negative direction.
FAQs on Kinematic Equations of Motion - Class 11 - CBSE/Schools
| 1. What are the three kinematic equations of motion? |  |
| 2. How are the kinematic equations derived? |  |
| 3. Can the kinematic equations be used for any type of motion? |  |
| 4. What are the units of the variables in the kinematic equations? |  |
| 5. How can the kinematic equations be used to solve numerical problems? |  |

|
Explore Courses for CBSE/Schools exam
|

|
















