Kinetic Theory of Gases: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q1: One mole of gas is contained in cube of side 0.2m.if these molecules, each of mass 5 x 10-26kg, moves with translation speed 1 483ms-1 ,calculate the pressure exerted by the gas on the side of cube .
Ans: Time interval between successive collision .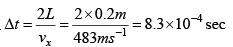
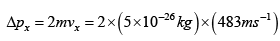 = 4.83 x1023 N-S
= 4.83 x1023 N-S
Force exerted for one molecule 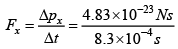 = 0.582 x 10-19N
= 0.582 x 10-19N
Total force exerted by one mole gas is ( 6 x1023 ) x ( 0.582 x 10-19 N ) = 3.49 x 104N
Average pressure is given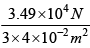 = 2.95 x 105 NM-2
= 2.95 x 105 NM-2
Q.2. Calculate the fraction of gas molecules which have the mean–free path in the range λ to 2λ .
Ans: The fraction of gas molecules that do not undergoes collision after path length x is 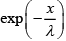 . Therefore the fraction of molecules that has free path values between λ to 2λ is
. Therefore the fraction of molecules that has free path values between λ to 2λ is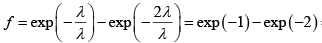 = 0.37 - 0.14 = 0.23
= 0.37 - 0.14 = 0.23
Q.3. The molecules of a gas move an average speed of 1 450ms-1 . If η = 16.6 x 10-6 Nsm-2, ρ = 1.25kgm-3 and n = 2.7 x 1025 m-3. Calculate the mean free path and diameter of the gas molecules.
Ans: We can write as
λ = 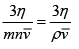
On inserting the given numerical values, we get
λ = 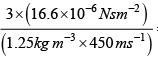 = 8.85 x 10-8m
= 8.85 x 10-8m
λ = 
We can invert this relation to express d in terms of λ :
d = 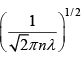 =
= 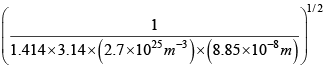 = 3.42 x 10-10m
= 3.42 x 10-10m
Q.4. (a) Three closed vessel A, B and C at the same temperature T and contains gases which obey the MB distribution of velocities. Vessel A contains only O2 , B only N2 and C a mixture of equal quantities O2 and N2 . If the average speed of the O2 molecules in vessel A is v1 , that of N2 molecules in vessel B in v2 , calculate the average speed of the molecules in vessel C
(b) The temperature of an ideal gas is increased from 120K to 480K . The rms velocity of the gas molecules is v , at 480K Calculate the rms velocity of the gas molecule.
Ans: (a) The average speed of molecules of an ideal gas is given by for same gas.
for same gas.
Since, the percentage of A & C are same, average speed of O2 molecules will be equal in A & C i.e. v1 .
(b) 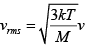
= 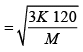
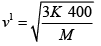
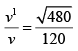
v1 = 2v
Q.5. (a) Two identical containers A and B with friction less pistons contain the same ideal gas at the same temperature and same volume V . The mass of the gas in A is mA and that in B is mB . The gas in each cylinder is allowed to expand isothermally to the same volume 2V . The changes in the pressure in A & B are found to be ΔP and 1.5ΔP respectively. Then find the ratio 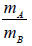
(b) Find the ratio of the speeds of sound in nitrogen gas to that in helium gas, at 300K
Ans: (a) Process is isothermal. Therefore, T = constt × 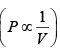 volume is increasing, therefore pressure will decrease.
volume is increasing, therefore pressure will decrease.
In Chamber (A)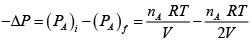
= 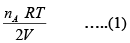
In Chamber (B) 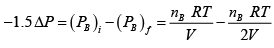
= 
From (1) & (2) 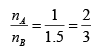
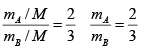
3mA = 2mB
(b) v = 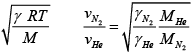
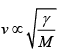
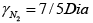
= 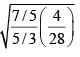
= √3/5
Q.6. Plot the Density of states as a function of energy and momentum in three, two and one dimensional systems.
(a) 3D
(b) 2D
(c) 1D
Ans: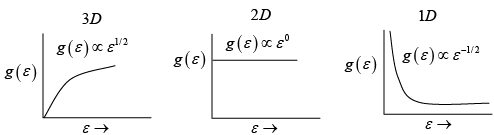
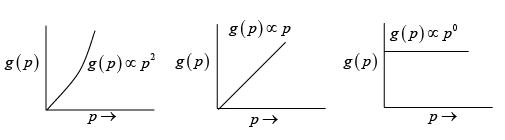
Q.7. In the interstellar space, the density of hydrogen molecule H2 is about one molecule / cm3 .Taking the diameter of H2 approximately 1A0 , calculate
(a) Average velocity of the molecule at kinetic temperature is 100K
(b) Mean free path of the H2 molecules
(c) Collision frequency
Ans: ρ = 1 molecule / cm3 diameter d = 1A0 T = 300K
m = 2x (1.67 x 10-24) = 3.34 x 10-24 gm
(a) Average velocity 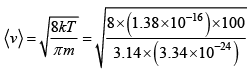 = 1 x 105cm/sec
= 1 x 105cm/sec
(b) Mean free path λ = 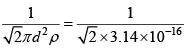 = 2 x 1015 cm
= 2 x 1015 cm
(c) v = 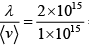 = 2 collision per second
= 2 collision per second
Q.8. The mean free path of the molecules of a gas at a pressure p and temperature T is 3x107m . Calculate the mean free path if
(a) the temperature is doubled and
(b) the pressure is doubled.
Ans: (a) We know
λ = 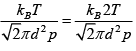
When the temperature is doubled, we note that the mean free path will increase by a factor of two. Hence, 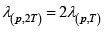 = 6 x10-7 m
= 6 x10-7 m
(b) When the pressure is doubled, the mean free path will be halved: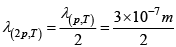 = 1.5 x10-7 m
= 1.5 x10-7 m
Q.9. (a) At the room temperature, the rms speed of the molecules of a certain diatomic gas is found to be 1930m/ s . What is the name of the gas?
(b) If one mole of a monatomic gas (γ = 5/ 3) is mixed with one mole of a diatomic gas (γ = 7/ 5) . Calculate the value of γ for the mixture?
Ans: (a) 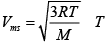 = 300K
= 300K
1930m/s = 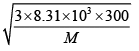
M = 2 g/ mol or the gas is H2 .
(b) γ1 = 5/3 means gas monatomic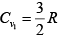
γ2 = 7/5 means gas diatomic 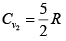
Cv (for mixture) = 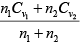
= 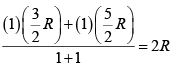
Cp = Cv + R = 3R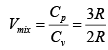 = 1.5
= 1.5
Q.10. (a) The average translational energy and the rms speed of molecules in a sample of oxygen gas at 300K are 6.21x10-21 J & 484m/ s respectively. The corresponding values at 600K are nearly (assuming ideal gas behavior)
(b) The average translational energy of O2 (molar mass 32) molecules at a particular temperature is 0.048eV . Calculate the translation K.E. of N2 (molar mass 28 ) molecules in eV at the same temperature?
(c) A vessel contains 1mole of O2 gas (molar mass 32) at a temperature T . The pressure of the gas is P' . An identical vessel containing one mole of the gas (molar mass 4 ) at a temperature 2T , Calculate the pressure.
(d) A vessel contains a mixture of one mole of O2 & two moles of N2 at 300K .
Calculate the ratio of the average rotational kinetic energy per O2 molecule to per N2 molecule.
Ans: (a) 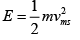
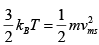
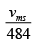 = √2
= √2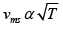
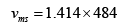
 = 684.37m/s
= 684.37m/s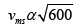
K.E = 6.21 x 2 x10-21 J
= 12.42 x 10-21 J
(b) Average translational energy of an ideal gas molecule is 3/2kT which depends on temperature only, Therefore if same temperature 0.048eV
(c) PV = μ RT
P ∝ T
P' = 2P
(d) Average kinetic energy per molecule per degree of freedom= 1/2kT. Since, both the gases are diatomic and at same temperature ( 300K ), both will have same rotational DOF = 2 therefore, both the gases will have the same average rotational K ×E× per molecule
=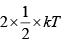 = kT
= kT
Q11: If a black body emits photon at the rate of 1600 Js-1 at 527°C what will be the rate of emission of photon by the same body when its temperature is 127°C
(a) 100 J/s
(b) 200 J/s
(c) 250 J/s
(d) More than one of the above
(e) None of the above
Ans: 100 J/s
Concept:
A black body is an object that absorbs all the radiant energy reaching its surface. No actual body is perfectly black; the concept of a black body is an idealization with which the radiation characteristics of real bodies can be compared.
Properties of the black body:
- It absorbs all the incident radiation falling on it and does not transmit or reflect regardless of wavelength and direction
- It emits the maximum amount of thermal radiation at all wavelengths at any specified temperature
- It is a diffuser emitter (i.e. the radiation emitted by a black body is independent of direction)
Stefan's Law: According to it the radiant energy emitted by a perfectly black body per unit area per sec (i.e. emissive power of black body) is directly proportional to the fourth power of its absolute temperature i.e.
E ∝ T4 ⇒ E = σT4
Here,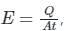 Thus this equation is also known as Intensity of radiated energy
Thus this equation is also known as Intensity of radiated energy
Whereas, 
Here R is the rate of radiation emitted and for this the equation can be modified as
R = AσT4
The value of Stefan's constant is 5.67 × 10-8 W/m2 K4.
Where,
σ = a constant called Stefan’s constant,
T = temperature of black-body
E = energy radiated per unit area per unit time.
Q = Amount of heat radiation emitted by perfectly black body.
t =Time for which black body radiates emitted
A = surface area of Black body
Calculation:
Given that,
Rate of emission of photon at 527°C, R1 = 1600 Js-1
Temperature of surface, T2 = 127°C = 127 + 273 = 400 K
Temperature of surface, T1 = 527°C = 800 K
Now according to Stefan’s Law
R = AσT4
By substituting the given value
Q12: Find the amount of heat required to increase the temperature of 5 mole of water by 10°C.
(a) 4.5R
(b) 45R
(c) 450R
(d) More than one of the above
(e) None of the above
Ans: 450R
CONCEPT:
Specific heat capacity of water:
- We can use the law of equipartition of energy to determine the specific heat of the water.
- We treat water like a solid.
- We consider every atom vibrating about its mean position. So the average energy of each atom is given as,
⇒ E = 3kBT
- The water molecule has three atoms, two hydrogens, and one oxygen.
- If NA is the number of molecules in one mole of water, then the average energy of one mole of water is given as,
⇒ U = 9NAkBT = 9RT
Where kB = Boltzmann constant, T = absolute temperature, and R = universal gas constant
- So the molar specific heat of water is given as,
⇒ C = 9R
- This is the value observed and the agreement is very good.
- In the calorie, gram, degree units, water is defined to have unit specific heat.
- The predicted specific heats are independent of temperature.
CALCULATION:
Given N = 5 mole and ΔT = 10°C
- According to the law of equipartition of energy, the molar specific heat of water is given as,
⇒ C = 9R
Where R = universal gas constant
- So the amount of heat required to increase the temperature of N mole of water by ΔT temperature is given as,
⇒ E = NCΔT
⇒ E = 5 × 9R × 10
⇒ E = 450R
- Hence, option 3 is correct.
Q13: For an adiabatic expansion of an ideal gas, the fractional change in its pressure is equal to (where γ is the ratio of specific heats) :
(a)
(b)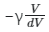
(c)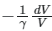
(d) More than one of the above
(e) None of the above
Ans: 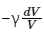
CONCEPT
- An adiabatic expansion is the thermodynamic process in which no exchange in energy or matter is allowed.
- The equation of state for an adiabatic change is PVγ = constant.
EXPLANATION
We know,
PVγ = constant.
Differentiating on both sides,
VγdP +PγVγ-1dV = 0
Diving by Vγ/P we have,
dP/P + γ dv/V = 0
so, dP/P = - 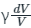
So, the correct answer is option (1).
Q14: The molecule of a monatomic gas has only three translational degrees of freedom. Thus, the average energy of a molecule at temperature 'T' is ____________.
(a) 3kBT
(b) (3/4) kBT
(c) (1/3)kBT
(d) (3/2)kBT
Ans: (3/2)kBT
CONCEPT:
- According to kinetic energy theory, if we increase the temperature of a gas, it will increase the average kinetic energy of the molecule, which will increase the motion of the molecules.
- This increased motion increases the outward pressure of the gas.
The average kinetic energy (KE) or energy (E) of translation per molecules of the gas is related to temperature by the relationship: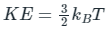 (degree of freedom of a monoatomic gas = 3)
(degree of freedom of a monoatomic gas = 3)
Where K E = kinetic energy, kB = Boltzmann constant and T = temperature.
EXPLANATION:
The average energy of a molecule is given by:
KE = E = (3/2)kBT
So option 4 is correct.
Q15: What is the relation between Kinetic energy (E) of a gas and its pressure (P)?
(a)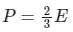
(b)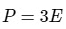
(c)
(d)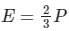
Ans:
CONCEPT:
- The pressure in a gas developed due to the collisions between the gaseous molecules.
- The energy possessed by the molecule of the gas due to its motion is called kinetic energy of the gas molecules.
From the kinetic theory of gases, the pressure (P) exerted by an ideal gas is given by
where ρ is the density of ideal gas and C is its root mean square velocity.
We know, density = mass/volume which implies that mass = density × volume. So, for a unit volume of gas, mass= ρ × 1 = ρ
Now, the mean kinetic energy of translation per unit volume of gas (E) = 
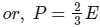
EXPLANATION:
The pressure(P) that is exerted by an ideal gas is equal to two-thirds of the mean kinetic energy of translation(E) per unit volume of the gas: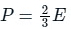
So option 1 is correct.
|
6 videos|20 docs|32 tests
|
FAQs on Kinetic Theory of Gases: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is the kinetic theory of gases? |  |
| 2. How does the kinetic theory of gases explain pressure? |  |
| 3. What assumptions are made in the kinetic theory of gases? |  |
| 4. How does the kinetic theory of gases explain temperature? |  |
| 5. Can the kinetic theory of gases explain deviations from ideal behavior? |  |
















