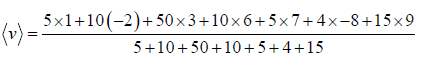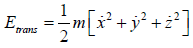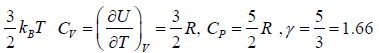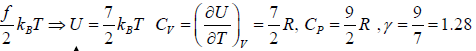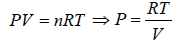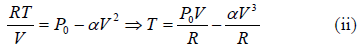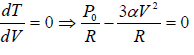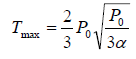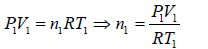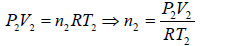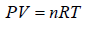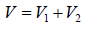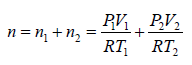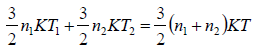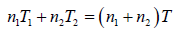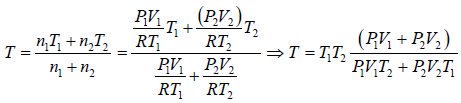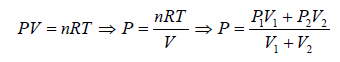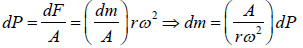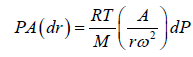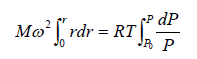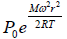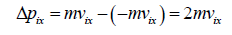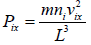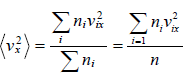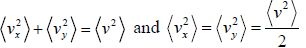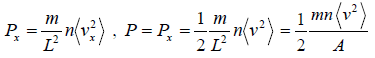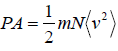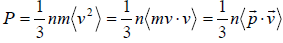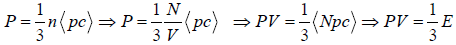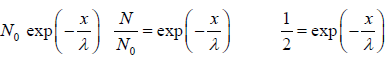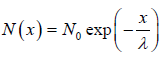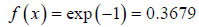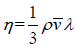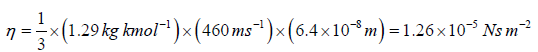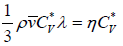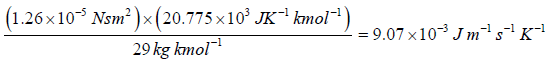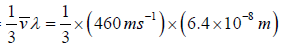Kinetic Theory of Gases | Kinetic Theory & Thermodynamics - Physics PDF Download
Kinetic theory is a basic mathematical modeling that bridges mechanics and
thermodynamics.
Postulates of kinetic theory of gases
- Matter is made up of identical molecules.
- Thermal energy can be identified with molecular motion.
Methodology
Using laws of classical mechanics and statistical averaging one can find total energy of Ideal gases. We can use this theory to study viscosity, conduction, diffusion, effusion and Brownian motion.
Basic Assumption of Kinetic Theory
1. Any infinitely small volume of a gas contains a large number of molecules. The order of number of molecule is 1023
2. A gas is made up of identical molecules, which behaves as rigid, perfectly elastic, hard sphere but considered as point mass .
The diameter of molecule is order of 10-10m at STP
3. The molecules continuously moves in random directions. All direction of motion are equally probable.
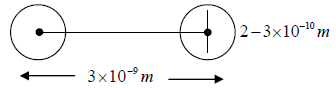
4. The size of the molecules is much less than the average distance between them. The average distance between them is order of 10-9m and diameter is of order of 10-10m.
5. The molecule of a gas exerts no force on each other except when they collide. These forces are due to only exchange of momentum during collision
6. The collision between molecules and with walls are perfectly elastic.
7. The molecular velocities are assumed to be uniformly distributed in all directions, which means velocity is isotropic symmetric and there is not any preferential direction.
8. The molecules move with all speeds ranging from 0 to ∞.
9. The time of collision is much less than the time between collisions.
Basic Statistical Formula to be used for Kinetic Theory:
If there is a sample random variable X = 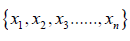
And total number of variable is N , then some statistical phenomena is defined as Mean Value:
If group of
n1 number of x1
n2 number of x2
...
nn number of xn
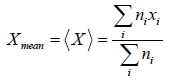
Root mean square value 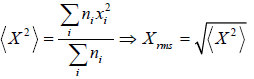
ΔX = 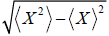 is identified as standard deviation
is identified as standard deviation
Example 1: Consider a system of particles and its velocities in one-dimension given in the table.
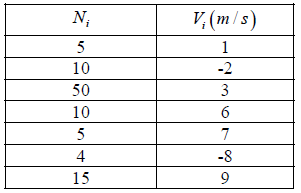
Find:
(a) Average velocity
(b) Root Mean Square velocity
(c) Most probable velocity
(a)
3.36m/ s
(b)
= 25 9697
(c) vp = 3 m/s most number of particles are having velocity 3 m/s
Pressure Exerted by a Gas
Suppose there are N molecules per cubic meter each of mass m and it is assumed that ni number of molecule have velocity vi .
Mathematically, and
and 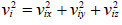 , where vix,, viy and viz are x, y and z components of velocity of gases respectively
, where vix,, viy and viz are x, y and z components of velocity of gases respectively
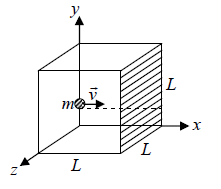
Figure 1, shows a typical gas molecule, of mass m and velocity 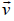 , that is about to collide with the shaded wall, where the time Δt between collisions is the time the molecule take to travel to the opposite wall and back again at speed vix.
, that is about to collide with the shaded wall, where the time Δt between collisions is the time the molecule take to travel to the opposite wall and back again at speed vix.
From assumptions of kinetic theory of gases, 
Suppose, molecules are kept in the cubic container of parameter L .
A molecule moving in the x - direction will have momentum mvix normal to face of the cube before collision.
Hence, the momentum Δpix delivered to the wall by the molecule during collision is
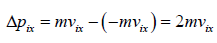
Force acting on the wall by molecule is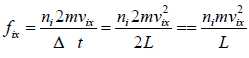
Pressure exerted on the walls of container by molecules, 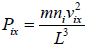
So, the pressure in the x - direction exerted by all molecules is,
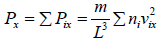
Average value of v2 is given by,
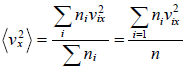
For three dimensional system, 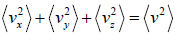 and
and
For isotropic system, 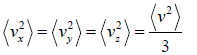
So, Px can be written as
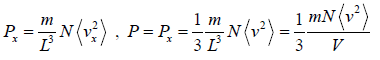
PV = 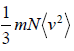
where V is volume of the container and (v2) is average value of square of velocity.
Gas Law for Ideal Gases
Boyle’s Law
At constant temperature (T), the pressure (P) of a given mass of a gas is inversely proportional to its volume (V) i.e. 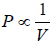

Charle’s Law at constant pressure and Gay Lussac’s law at constant volume
At constant pressure (P) the volume of a given mass of a gas is proportional to its temperature (T), V ∝ T.
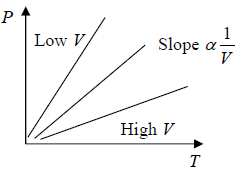
At constant volume (V) the Pressure of a given mass of a gas is proportional it temperature (T), P ∝ T.
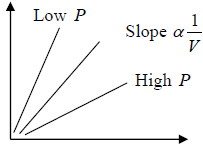
Avogadro’s Law
At the same temperature and pressure, equal volume of all gases contain equal number of molecules (N)
N1 = N2
Graham’s Law of Diffusion
When two gases at the same pressure and temperature are allowed to diffuse into each
other, the rate of diffusion (r) of each gas is inversely proportional to square root of density of gas (ρ)
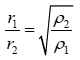
Dalton’s Law of Partial Pressure
The sum of pressure exerted (P) by each gas occupying the same volume as that of the mixture (P1,P2,P3,....) where P = P1 + P2 + P3+...
Ideal Gas Equation
Consider a sample of an Ideal gas at pressure P , volume V and temperature T, the gas follows the equation
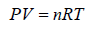
where, n is the number of molecules and R is proportionality constant known as gas constant
R = 8.314 J/mol/K
Boltzmann constant K is ratio between R to Avogadro number NA i.e.
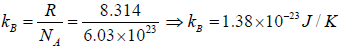
Kinetic Interpretation of Temperature
According to the assumption of kinetic theory of gases, there is only translation motion of the molecule and there is not any potential acting between them, so
Average Energy (E) of gases are equivalent to average translational energy of a molecule i.e. 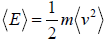
Pressure, PV = 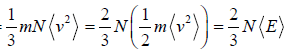
= 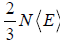 where PV = nRT
where PV = nRT 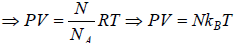
= 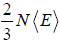 put value of PV =
put value of PV = 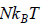
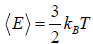 , where kB is Boltzmann constant kB = 1.38 x 1023 J/K
, where kB is Boltzmann constant kB = 1.38 x 1023 J/K
So, average kinetic energy is given by (E) = 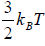 , where T is absolute temperature
, where T is absolute temperature
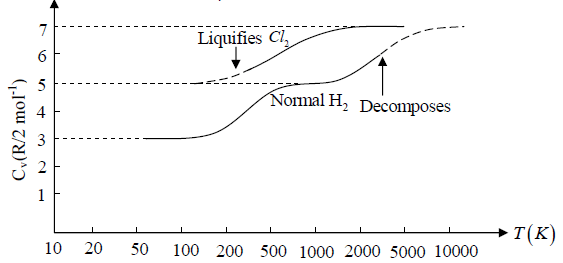
Internal energy of gases with degree of freedom
Number of independent coordinates required to specify its position correctly
f = 3N - k
Where N is number of particles and k is Total number of constraints. For a system in
equilibrium at temperature T , the total energy is equally partitioned among the different degrees of freedom and Energy associated with each degree of freedom is 1/2kBT. If there is f degree of freedom then internal energy of system molecule is U = 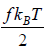
If U is internal energy of Ideal gas then specific Heat at constant volume is defined as 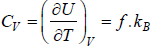
Example 2: Mono atomic gas in three dimensional volume:
f = 3x1- 0 = 3⇒ f = 3
U =
Example 3: Diatomic molecule at low temperature:
At low temperature Diatomic molecule can be under stood by a model in which two points mass are connected by a mass less rod .so distance between both of particle is constant so k = 1
So, degree of freedom is f = 3 x 2 -1 = 5
U =
Example 4: Diatomic molecule at high temperature:
At high temperature Diatomic molecule can be under stood by a model in which two point mass are connected by a mass less spring. Due to spring one extra mode of degree of freedom(one due to potential energy) will excited hence
So degree of freedom is f =
= 7
U =
Example 5: Find the maximum attainable temperature of ideal gas in each process given by, 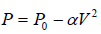 , where and P0 and α are positive constants, and V is the volume of one mole of gas.
, where and P0 and α are positive constants, and V is the volume of one mole of gas.
P = P0 - αV2 (i)
Number of moles of gas = 1
We know that,
Putting in (i),
For T maximum,
Putting in equation (ii), one will get
Example 6: Two thermally insulated vessel 1 and 2 are filled with air. They are connected by a short tube with a valve. The volume of vessels and the pressure and temperate of air in them are  respectively. Calculate the air temperate and pressure established after opening of valve, if air follows Ideal gas equation.
respectively. Calculate the air temperate and pressure established after opening of valve, if air follows Ideal gas equation.
For vessel (1),
For vessel (2),
After opening the valve, let pressure, volume and temperature are P, V and T respectively.
Hence, system is isolated and thus,
Energy of system (1) + energy of system (2) = energy of composite system
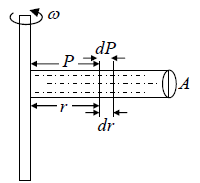
Example 7: A horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature equal to T and the molar mass of air equal to M. Find the air pressure as a function of the distance r from the rotation axis. The molar mass is assumed to be independent of r .
Force equation of dr element,
, if A is cross section area then
Also we know that , PV = nRT
P =
Example 8: Prove that, PA = 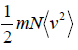 and
and 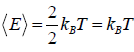 in two dimension.
in two dimension.
A molecule moving in the x direction will have momentum
normal to face of the cube before collision.
Hence, the momentum
delivered to the wall by the molecule during collision is,
Force acting on the wall by molecule is
Pressure exerted on the walls of container by molecule is,
So, the pressure in the x - direction exerted by all molecules is,
Average value of v2 is given by,
For two dimensional system
So,Px can be written as
Thus,
Example 9: It is possible to treat electromagnetic radiation in a container whose walls are mirror, as a gas of particle (photons) with a constant speed c and whose energy is related to their momentum p , which is directed parallel to their velocity by, E = pc . Show that if container is full of radiation, the equation of state is PV = 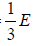
Pressure
For photon v = c and velocity is parallel to momentum, so
Mean Free Path (λ)
The Mean free path is the average distance travelled by molecule between two successive
collisions. If 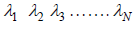 denotes successive free length path traversed in time t and N is total number of ion suffered in this period then mean free path λ given by
denotes successive free length path traversed in time t and N is total number of ion suffered in this period then mean free path λ given by 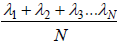 which is equivalent to total distance travelled divided by total number of collision.
which is equivalent to total distance travelled divided by total number of collision.
Consider two molecules of masses m1 and m2 diameters d1 and d2
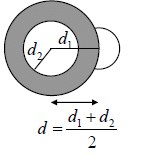
After collision they can be considered as one body system. Reduced mass, 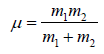 and centre to centre distance,
and centre to centre distance, 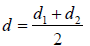
Let the number of densities of these gases = n1 and n2
We construct a cylinder of cross section area πd2, length 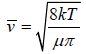 , which defines
, which defines
Average speed characterizing maxwellian molecules when molecule of first type moves it collides will all the molecules of second type in the cylinder.
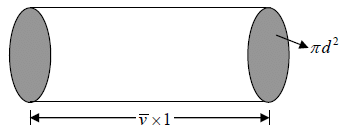
Total number of such collisions is given by 
= 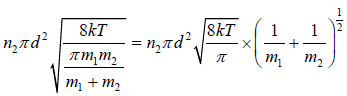
If all molecule will identical d1 = d2 = d , m1 = m2 = m and n1 = n2 = n
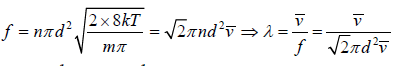
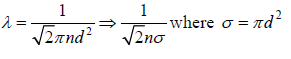
Distribution of Free Path
We wish to estimate the numbers that have not made a collision at some later time. Let the number of molecules surviving a collision in traveling a distance x be N = N(x). If N0 is number of molecule at x = 0 then number of molecule N = N(x) which will suffer no collision between distance x to 0 is N(x) = N0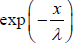 with mean path λ as parameter of gas.
with mean path λ as parameter of gas.
The equation N(x) = N0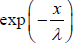 is identified as survival equation. For Maxwellian distribution into account the survival equation can be represented as
is identified as survival equation. For Maxwellian distribution into account the survival equation can be represented as
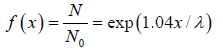
The survival equation is shown in figure.
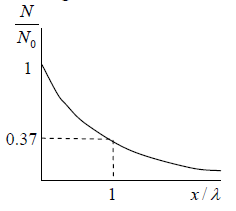
Example 10: The fraction of molecules that are undeflected is 1/2, then find the distance that undeflected particles will travel .
N =
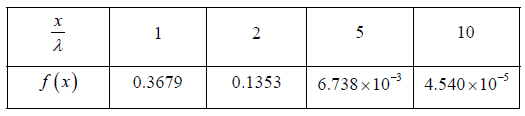
Example 11: In a sample of 1026 gas molecules, each molecule is moving with the same speed. Calculate the fraction of molecules that will continue to travel undeflected after traversing of λ,2λ,5λ and 10λ.
The values of f (x) are tabulated below for different below for distance traversed by the gas molecules and you can readily verify these using Eq.
To illustrate for x= λ we can write
We will note that after traversing a distance of λ and 2λ , nearly 37% and 13.5% molecules respectively survive collisions. However, after covering a distance of 10λ , almost all molecules will have undergone a collision.
Basic of Transport phenomenon
When a gas is endowed with mass motion, random molecular motion can lead to transport of energy, momentum or mass, depending on the physical conditions, which lead to the phenomena of thermal conduction, viscosity and diffusion, respectively.
Coefficient of viscosity (η) : The coefficient of viscosity for a gas having velocity gradient in a direction normal to the direction of mass motion is given by 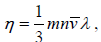 where m is the molecular mass and v' is the average speed of a molecule. At a given temperature, η is independent of pressure.
where m is the molecular mass and v' is the average speed of a molecule. At a given temperature, η is independent of pressure.
Thermal conductivity (K) : The thermal conductivity, K is given by 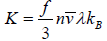 , where f denotes the number of degrees of freedom.
, where f denotes the number of degrees of freedom.
K and η are connected by the relation  , where M is molecular weight of gas.
, where M is molecular weight of gas.
Coefficient of diffusion (D) : The coefficient of diffusion D is given by
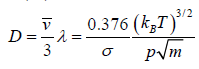
Example 12: Calculate the coefficient of viscosity, thermal conductivity and diffusion coefficient for air. Given ρ = 1.29kgm-3 , v' = 460 ms-1 and λ = 6.4x10-8m. Take molecular weight of air as 29kg kmol-1 and R = 8.31kJ K-1 kmol-1 .
We know that the coefficient of viscosity η is given by
That the coefficient of thermal conductivity K is given by K =
Here
is specific heat capacity per unit mass, and M = 29kg kmol-1
For a diatomic gas,
= 20.775 x 103 JK-1kmol-1. hence
K =
The coefficient of diffusion D is given as D =
= 9.8x10-6 m2 s-1
Phase space and Gibbs postulates and Density of state
Phase curve any between positions coordinate along horizontal axis and conjugate momentum along vertical axis for given value of energy is known as phase curve.
Gibbs take account of uncertain principle then Gibbs make postulates
The minimum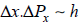 for one dimension
for one dimension
Minimum 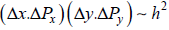 for two dimension
for two dimension
Minimum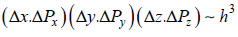 for two dimension
for two dimension
Density of State
g(E)dE is number of level (number of quantum state) in the range of E to E + dE then
g (E) is known as Density of state
Density of State in three dimension
where V is volume of container
which is equation of sphere with coordinate px, py, pz.
So, is volume of sphere with radius
is volume of sphere with radius 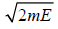
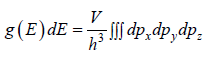 is equivalent to
is equivalent to 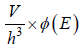
where ∅(E) volume of spherical shell between radius 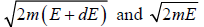
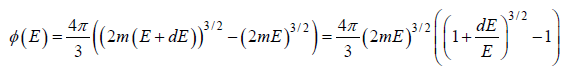
Using Taylor expansion then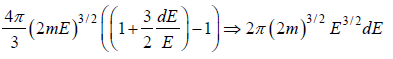
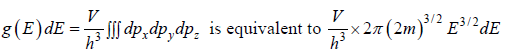
g(E)dE in three dimension g(E)dE = 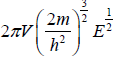 where V is volume of three dimensional space.
where V is volume of three dimensional space.
Density of State in Two Dimension
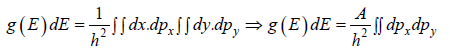
where A is volume of container 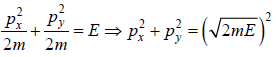
which is equation of circle with coordinate px , py
So, 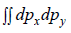 is area of circle with radius
is area of circle with radius 
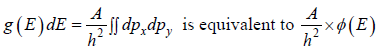
where ∅(E) volume of spherical shell between radius 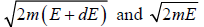
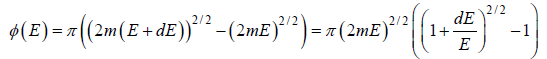
Using Taylor expansion, then 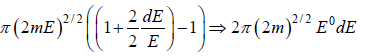
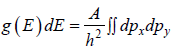 is equivalent to
is equivalent to 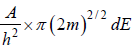
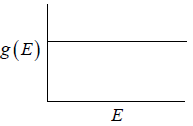
g(E)dE in two dimension g(E)dE = 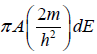 , where A is area of the two dimensional space.
, where A is area of the two dimensional space.
Density of State in One Dimension
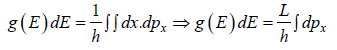
where A is volume of container 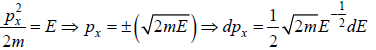
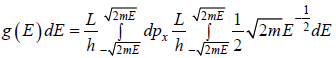
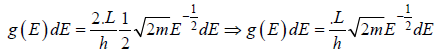
g(E)dE in one dimension g(E)dE = 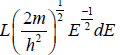 where L is area of the one dimensional space
where L is area of the one dimensional space
|
6 videos|20 docs|32 tests
|
FAQs on Kinetic Theory of Gases - Kinetic Theory & Thermodynamics - Physics
| 1. What are the postulates of the kinetic theory of gases? |  |
| 2. What is the gas law for ideal gases? |  |
| 3. What is the kinetic interpretation of temperature? |  |
| 4. What is the mean free path (λ) in the kinetic theory of gases? |  |
| 5. What is the density of state in three dimensions? |  |