Kondo effect | Basic Physics for IIT JAM PDF Download
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change in electrical resistivity with temperature. The effect was first described by Jun Kondo, who applied third-order perturbation theory to the problem to account for s-d electron scattering. Kondo's model predicted that the scattering rate of conduction electrons of the magnetic impurity should diverge as the temperature approaches 0 K.Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements like cerium, praseodymium, and ytterbium, and actinide elements like uranium. The Kondo effect has also been observed in quantum dot systems.
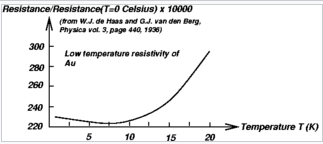
Kondo effect: How gold with a small amount of what were probably iron impurities behaves at low temperatures
Theory
The dependence of the resistivity p on temperature T, including the Kondo effect, is written as
where ρ0 is the residual resistivity, the term aT2 shows the contribution from the Fermi liquid properties, and the term bT5 is from the lattice vibrations: a, b, cm and μ are constants independent of temperature. Jun Kondo derived the third term with logarithmic dependence on temperature.
Background
Kondo's model was derived using perturbation theory, but later methods used non-perturbative techniques to refine his result. These improvements produced a finite resistivity but retained the feature of a resistance minimum at a non-zero temperature. One defines the Kondo temperature as the energy scale limiting the validity of the Kondo results. The Anderson impurity model and accompanying Wilsonian renormalization theory were an important contribution to understanding the underlying physics of the problem. Based on the Schrieffer-Wolff transformation, it was shown that Kondo model lies in the strong coupling regime of the Anderson impurity model. The Schrieffer-Wolff transformation projects out the high energy charge excitations in Anderson impurity model, obtaining the Kondo model as an effective Hamiltonian.
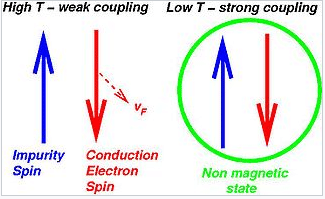
Schematic of the weakly coupled high temperature situation in which the magnetic moments of conduction electrons in the metal host pass by the impurity magnetic moment at speeds of vF, the Fermi velocity, experiencing only a mild antiferromagnetic correlation in the vicinity of the impurity. In contrast, as the temperature tends to zero the impurity magnetic moment and one conduction electron moment bind very strongly to form an overall non-magnetic state.
The Kondo effect can be considered as an example of asymptotic freedom, i.e. a situation where the coupling becomes non-perturbatively strong at low temperatures and low energies. In the Kondo problem, the coupling refers to the interaction between the localized magnetic impurities and the itinerant electrons.
Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements like cerium, praseodymium, and ytterbium, and actinide elements like uranium. In heavy fermion materials, the nonperturbative growth of the interaction leads to quasi-electrons with masses up to thousands of times the free electron mass, i.e., the electrons are dramatically slowed by the interactions. In a number of instances they actually are superconductors. More recently, it is believed that a manifestation of the Kondo effect is necessary for understanding the unusual metallic delta-phase of plutonium.
More recently the Kondo effect has been observed in quantum dot systems. In such systems, a quantum dot with at least one unpaired electron behaves as a magnetic impurity, and when the dot is coupled to a metallic conduction band, the conduction electrons can scatter off the dot. This is completely analogous to the more traditional case of a magnetic impurity in a metal.
In 2012, Beri and Cooper proposed a topological Kondo effect could be found with Majorana fermions, while it has been shown that quantum simulations with ultracold atoms may also demonstrate the effect.
In 2017, teams from the Vienna University of Technology and Rice University conducted experiments into the development of new materials made from the metals cerium, bismuth and palladium in specific combinations and theoretical work experimenting with models of such structures, respectively. The results of the experiments were published in December 2017 and, together with the theoretical work, lead to the discovery of a new state , a correlation-driven Weyl semimetal. The team dubbed this new quantum material Weyl-Kondo semimetal.
|
210 videos|156 docs|94 tests
|
FAQs on Kondo effect - Basic Physics for IIT JAM
| 1. What is the Kondo effect? |  |
| 2. How does the Kondo effect occur? |  |
| 3. What are the implications of the Kondo effect? |  |
| 4. How does the Kondo effect affect electronic devices? |  |
| 5. Can the Kondo effect be controlled or manipulated? |  |

|
Explore Courses for Physics exam
|

|

















