Lab Manual: Verify that if Two Lines Intersect Each Other | Lab Manuals for Class 9 PDF Download
Objective
To verify experimentally that if two lines intersect each other, then(i) the vertically opposite angles are equal.
(ii) the sum of two adjacent angles is 180°.
(iii) the sum of all the four angles is 360°.
Materials Required
Cardboard, White paper, A full protractor, A nail, Two transparent strips marked as AB and CD, Adhesive
Prerequisite Knowledge
(i) Basic knowledge of lines and angles.
(ii) Pair of angles; adjacent angles, linear pair of angles, vertically opposite angles.
Theory
1. Lines and Angles- Line Segment: A part of a line with two end points, is called a line segment. Line segment AB is denoted by
 .
. A line segment has a definite length, which can be measured. The line segment
A line segment has a definite length, which can be measured. The line segment  is the same thing as the line segment
is the same thing as the line segment  .
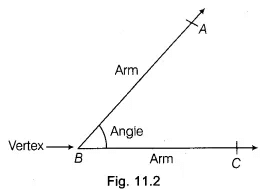
. - Angle: The figure formed by two rays with the same initial point, is called an angle.
In Fig. 11.2, the common initial point B is known as the vertex of the angle and the rays forming the angle are called its arms or sides.
 There are different types of angles such as acute angle, right angle, obtuse angle, straight angle, reflex angle and complete angle, which are discussed below :
There are different types of angles such as acute angle, right angle, obtuse angle, straight angle, reflex angle and complete angle, which are discussed below :Acute Angle: An angle whose measure is more than 0° but less than 90°, is called an acute angle.
 In Fig. 11.3, ∠AOB is an acute angle.
In Fig. 11.3, ∠AOB is an acute angle.
Since, 0° < ∠AOB < 90°Right Angle: An angle whose measure is 90°, is called a right angle.
 In Fig. 11.4, ∠AOB is a right angle and BO ⊥ OA.
In Fig. 11.4, ∠AOB is a right angle and BO ⊥ OA.Obtuse Angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.
 In Fig. 11.5, ∠AOB is an obtuse angle.
In Fig. 11.5, ∠AOB is an obtuse angle.
Since, 90° < ∠AOB < 180°Straight Angle: An angle whose measure is 180°, is called a straight angle. In Fig. 11.6, ∠AOB = 180° is a straight angle.
 A straight angle has two right angles.
A straight angle has two right angles.Reflex Angle: An angle whose measure is more than 180° but less than 360°, is called a reflex angle.
 In Fig. 11.7 and Fig. 11.8, ∠AOB and ∠PQR are reflex angles.
In Fig. 11.7 and Fig. 11.8, ∠AOB and ∠PQR are reflex angles.
180° < reflex ∠AOB < 360°
180° < reflex ∠PQR < 360°
Complete Angle: An angle whose measure is 360°, is called a complete angle. In Fig. 11.9, ∠AOA = 360° is a complete angle.

2. Pair of Angles
There are some relations between the angles which are described below:
- Adjacent Angles: Two angles are called adjacent angles, if
- they have a common vertex,
- they have a common arm and
- their non-common arms are on different sides of the common arm.
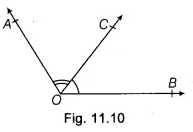
In Fig. 11.10, ∠AOC and ∠COB are adjacent angles because these angles have a common vertex 0, a common arm OC and non-common arms OA and OB are on different sides of the common ray OC. When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. So, here ∠AOB = ∠AOC + ∠COB.Note Here, ∠AOB and ∠AOC are not adjacent angles because their non-common arms OC and OB lie on the same side of the common arm OA
When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. So, here ∠AOB = ∠AOC + ∠COB.Note Here, ∠AOB and ∠AOC are not adjacent angles because their non-common arms OC and OB lie on the same side of the common arm OA
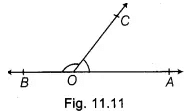
- Linear Pair of Angles: If the non-common arms of two adjacent angles form a line, then these angles are called linear pair of angles.
In Fig. 11.11, ∠AOC and ∠BOC form a linear pair of angles.
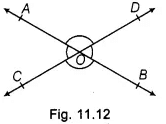
- Vertically Opposite Angles: Two angles are called a pair of vertically opposite angles, if their arms form two pairs of opposite rays.
In other words, when two lines intersect each other at a point, then there are two pairs of vertically opposite angles.
In Fig. 11.12, lines AB and CD intersect each other at 0. So, ∠AOC and ∠BOD are vertically opposite angles. Also, ∠AOD and ∠BOC are vertically opposite angles.
Procedure
- Take a cardboard of suitable size and by using adhesive paste a white paper on it.
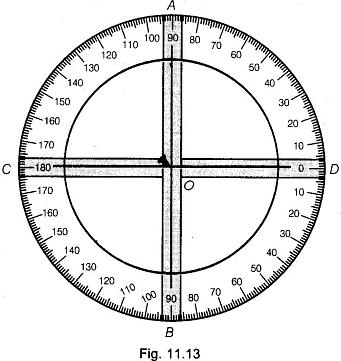
- Also, paste a full protractor (0° to 360°) with the help of adhesive on the cardboard. (see Fig. 11.13)

- Mark the centre of protractor as O.
- Now, make a hole in the middle of both transparent strips which contain two intersecting lines.
- Fix both strips at 0 by putting a nail, (see Fig. 11.13)
Demonstration
In the different positions of the strips, observe the adjacent angles and the vertically opposite angles.
In the different positions, also compare vertically opposite angles formed by the two lines.
Check the relationship between the vertically opposite angles.
Check whether the vertically opposite angles, ∠AOD and ∠COB are equal.
Similarly, check whether the vertically opposite angles, ∠BOD and ∠AOC are equal.
Find the sum of two adjacent angles such that ∠AOD + ∠AOC which is equal to 180°.
i.e. ∠AOC + ∠COB = ∠COB + ∠BOD
= ∠BOD + ∠AOD =180°
Now, we obtain the sum of all the four angles formed at the point 0 and it is equal to 360°.
Observation
In one position of the strips, by actual measurement of angles
- ∠AOD = ……… , ∠AOC = ……… ,
∠COB = ……… , ∠BOD = ……… ,
Hence, ∠AOD = ∠COB and ∠AOC = ∠BOD (vertically opposite angles) - ∠AOC + ∠AOD = ……… , ∠AOC + ∠BOC = ……… ,
∠COB + ∠BOD = ……… , ∠AOD + ∠BOD = ……… (linear pairs) - ∠AOD + ∠AOC + ∠COB + ∠BOD = ……… (angles formed at a point)
Result
We have verified experimentally that if two lines intersect each other, then
- the vertically opposite angles are equal.
- the sum of two adjacent angles is 180°.
- the sum of all the four angles is 360°.
Application
These properties are very useful in several geometrical operations.
|
15 videos|98 docs
|

|
Explore Courses for Class 9 exam
|

|
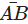 .
. A line segment has a definite length, which can be measured. The line segment
A line segment has a definite length, which can be measured. The line segment 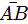 is the same thing as the line segment
is the same thing as the line segment 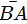 .
. There are different types of angles such as acute angle, right angle, obtuse angle, straight angle, reflex angle and complete angle, which are discussed below :
There are different types of angles such as acute angle, right angle, obtuse angle, straight angle, reflex angle and complete angle, which are discussed below :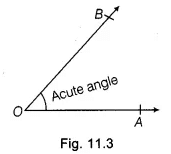 In Fig. 11.3, ∠AOB is an acute angle.
In Fig. 11.3, ∠AOB is an acute angle.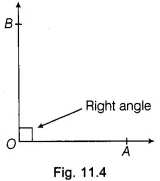 In Fig. 11.4, ∠AOB is a right angle and BO ⊥ OA.
In Fig. 11.4, ∠AOB is a right angle and BO ⊥ OA.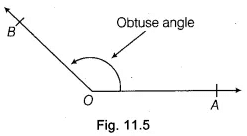 In Fig. 11.5, ∠AOB is an obtuse angle.
In Fig. 11.5, ∠AOB is an obtuse angle.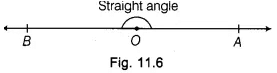 A straight angle has two right angles.
A straight angle has two right angles.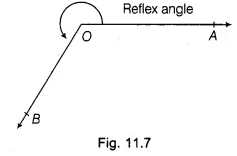 In Fig. 11.7 and Fig. 11.8, ∠AOB and ∠PQR are reflex angles.
In Fig. 11.7 and Fig. 11.8, ∠AOB and ∠PQR are reflex angles.

 When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. So, here ∠AOB = ∠AOC + ∠COB.Note Here, ∠AOB and ∠AOC are not adjacent angles because their non-common arms OC and OB lie on the same side of the common arm OA
When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. So, here ∠AOB = ∠AOC + ∠COB.Note Here, ∠AOB and ∠AOC are not adjacent angles because their non-common arms OC and OB lie on the same side of the common arm OA