Lab Manual: Verify the Algebraic Identity a³ + b³ = (a + b)(a²- ab + b²) | Lab Manuals for Class 9 PDF Download
Objective
To verify the identity a3 + b3 = (a + b) (a2 – ab + b2) geometrically by using sets of unit cubes.Prerequisite Knowledge
- Volume of cube = (edge)3
- Volume of cuboid = I x b x h
Materials Required
A set of 56 cubes each has dimensions (1 x 1 x 1) cubic unit. Cubes may be of wood, plastic, cardboard or thermocol.
Procedure
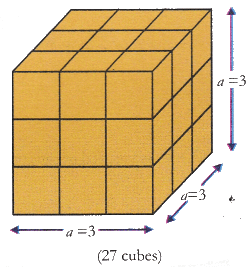
To verify the identity a3 + b3, we shall take a = 3 units and b = 1 unit.
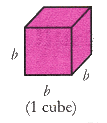
- Make an arrangement of 28 cubes such that we get a cube of 3 x 3 x 3 cubic units and a single unit cube of b = 1 unit as shown in fig. (i) and fig.(ii).

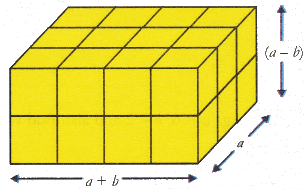
- Now we will use second set of 28 cubes. Consider one stack (24 cubes) as {a x (a+b)} cubic units i.e., (3 x 4 x 2) cu. units and arrange as shown in fig. (iii):

Fig. (iii)
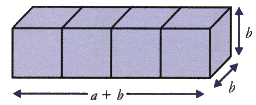
- Consider an other stack of 4 cubes such as (a + b) (b) (b) i.e., (4) (1) (1) cubic units. Arrange them as shown in fig. (iv).

Fig. (iv)
Observation and Calculation
As the arrangements shown in [fig. (i),fig. (ii)] and [fig. (iii), fig. (iv)], have equal number of cubes therefore the total volume in both the cases must be same.
In fig(i) and fig.(ii)
Volume of cube in fig. (i) = volume of 27 unit cubes = a3
Volume of cube of 1 unit = b3
Total volume of 28 cubes = a3 +b3 … (i)
In fig. (iii) and (iv),
Volume of cuboid of 24 unit cubes = (a + b) (a – b) (a)
Volume of cuboid of 4 unit cubes = (a + b)b2
Total volume of 28 cubes = (a+b) (a – b) (a)+(a+b) (b2)
= (a + b) (a2 – ab + b2) … (ii)
From (i) and (ii), we have
∴ a3 + b3 = (a + b) (a2 – ab + b2)
Result
The identity a3 + b3 = (a + b) (a2 – ab + b2) is verified geometrically by using cubes and cuboids.
Learning Outcome
Algebraic identity a3 + b3 = (a + b) (a2 – ab + b2) is verified geometrically. This activity can be performed by using different colours of cubes as shown in fig. (i), (ii), (iii) and (iv). We have learnt making of cuboids of various dimensions by using unit cubes and adding and subtracting cuboids.
Activity Time
By using different values of a and b, students can verify the identity a3 + b3, e.g., a = 6, b = 2 and also find volume of different cubes and cuboids used for this activity.
|
15 videos|98 docs
|

|
Explore Courses for Class 9 exam
|

|