Lagrange’s and Hamilton’s equations | Basic Physics for IIT JAM PDF Download
Elegant and powerful methods have also been devised for solving dynamic problems with constraints. One of the best known is called Lagrange’s equations. The Lagrangian L is defined as L = T − V, where T is the kinetic energy and V the potential energy of the system in question. Generally speaking, the potential energy of a system depends on the coordinates of all its particles; this may be written as V = V(x1, y1, z1, x2, y2, z2, . . . ). The kinetic energy generally depends on the velocities, which, using the notation vx = dx/dt = ẋ, may be written T = T(ẋ1, ẏ1, ż1, ẋ2, ẏ2, ż2, . . . ). Thus, a dynamic problem has six dynamic variables for each particle—that is, x, y, z and ẋ, ẏ, ż—and the Lagrangian depends on all 6N variables if there are N particles.
In many problems, however, the constraints of the problem permit equations to be written relating at least some of these variables. In these cases, the 6N related dynamic variables may be reduced to a smaller number of independent generalized coordinates (written symbolically as q1, q2, . . . qi, . . . ) and generalized velocities (written as q̇1, q̇2, . . . q̇i, . . . ), just as, for the rigid body, 3N coordinates were reduced to six independent generalized coordinates (each of which has an associated velocity). The Lagrangian, then, may be expressed as a function of all the qi and q̇i. It is possible, starting from Newton’s laws only, to derive Lagrange’s equations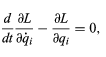 (94)
(94)
where the notation ∂L/∂qi means differentiate L with respect to qi only, holding all other variables constant. There is one equation of the form for each of the generalized coordinates qi (e.g., six equations for a rigid body), and their solutions yield the complete dynamics of the system. The use of generalized coordinates allows many coupled equations of the form to be reduced to fewer, independent equations of the form.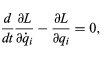 (94)
(94)
There is an even more powerful method called Hamilton’s equations. It begins by defining a generalized momentum pi, which is related to the Lagrangian and the generalized velocity q̇i by pi = ∂L/∂q̇i. A new function, the Hamiltonian, is then defined by H = Σi q̇i pi − L. From this point it is not difficult to derive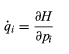 (95)
(95)
and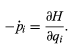 (96)
(96)
These are called Hamilton’s equations. There are two of them for each generalized coordinate. They may be used in place of Lagrange’s equations, with the advantage that only first derivatives—not second derivatives—are involved.
The Hamiltonian method is particularly important because of its utility in formulating quantum mechanics. However, it is also significant in classical mechanics. If the constraints in the problem do not depend explicitly on time, then it may be shown that H = T + V, where T is the kinetic energy and V is the potential energy of the system—i.e., the Hamiltonian is equal to the total energy of the system. Furthermore, if the problem is isotropic (H does not depend on direction in space) and homogeneous (H does not change with uniform translation in space), then Hamilton’s equations immediately yield the laws of conservation of angular momentum and linear momentum, respectively.
|
210 videos|156 docs|94 tests
|
FAQs on Lagrange’s and Hamilton’s equations - Basic Physics for IIT JAM
| 1. What are Lagrange's equations in physics? |  |
| 2. What are Hamilton's equations in physics? |  |
| 3. How do Lagrange's equations differ from Hamilton's equations? |  |
| 4. How are Lagrange's and Hamilton's equations related to each other? |  |
| 5. What are the advantages of using Lagrange's and Hamilton's equations in physics? |  |

|
Explore Courses for Physics exam
|

|

















