Lakhmir Singh & Manjit Kaur: Motion, Solutions- 4 | Science Class 9 PDF Download
Page No:42
Question 38:
Show by means of graphical method that: v = u + at, where the symbols have their usual meanings.
Solution :
Consider the velocity-time graph of a body shown in figure.
The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
Now, Initial velocity of the body, u= OA —–(1)
And,Final velocity of the body, v=BC ——(2)
But from the graph BC =BD + DC
Therefore, v=BD + DC ——(3)
Again DC = OA
So,v =BD + OA
Now, from equation (1), OA =u
So, v=BD + u ——(4)
We should find out the value of BD now. We know the slope of a velocity-time graph is equal to the acceleration, a.
Thus,Acceleration, a= slope of line AB
or a = BD/AD
But AD =OC= t, so putting t in place of AD in the above relation, we get:
or BD=at
Now, putting this value of BD in equation(4), we get:
v= u+ at
consider the velocity - time graph of a body shown in figure:

the body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in graph. The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
Now initial velocity of the body, u = OA --- (1)
and, final velocity of the body, v = BC --- (2)
But from the graph BC = BD+DC
Therefore v = BD+DC ----(3)
Again DC = OA
So, v = BD+ OA
Now, from equation (1), OA = u
So, v= BD+ u ----(4)
we should find out the value of BD now. We know the slope of the velocity -time graph is equal to the acceleration , a
Thus acceleration a = slope of line AB
or a = BD/AD
But AD = OC= t, so putting t in place of AD in the above relation, we get:

or BD = at
Now, Putting the value of BD in equation (4), we get
v= u+at
Question 39:
Show by using the graphical method that:  , where the symbols have their usual meanings.
, where the symbols have their usual meanings.
Solution :
Consider the velocity-time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC.
Suppose the body travels a distance s in time t. In the figure, the distance travelled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC. Thus:
Distance travelled = Area of figure OABC
= Area of rectangle OADC + area of triangle ABD
Now, we will find out the area of rectangle OADC and area of triangle ABD.
(i) Area of rectangle OADC =OA x OC
= u x t
=ut
(ii) Area of triangle ABD= (1/2)x Area of rectangle AEBD
= (1/2) x AD x BD
= (1/2) x t x at
= (1/2) at2
Distance travelled, s = Area of rectangle OADC + area of triangle ABD
Consider the velocity-time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity become v which is equal to BC in the graph. The time t is represented by OC.

Suppose the body travel a distance in time t . in the figure, the distance travelled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC. Thus:
Distance travelled = Area of figure OABC
= Area of rectangle OADC+ area of triangle ABD



Question 40:
Derive the following equation of motion by the graphical method : v2 = u2 + 2as, where the symbols have their usual meanings.
Solution :
Consider the velocity-time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
The distance travelled s by a body in time t is given by the area of the figure OABC which is a trapezium.
Distance travelled, s= Area of trapezium OABC
Now, OA + CB = u + v and OC =t Putting these values in the above relation, we get:
Eliminate t from the above equation. This can be done by obtaining the value of t from the first equation of motion.

Consider the velocity of time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. the time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE
the distance travelled s by a body in time t is given by the area of the figure OABC which is trapezium.

Now, OA +CB = u+v and OC = t putting these values in the above relation, we get:

Eliminate t from the above equation. This can be done obtaining the value of t from the first equation of motion.
thus v = u +at (first equation of motion)
and at = v
Page No:43
Question 53:
The graph given alongside shows the positions of a body at different times. Calculate the speed of the body as it moves from :
(i) A to B,
(ii) B to C, and
(iii) C to D.

Solution :
(i) The distance covered from A to B is( 3-0) =3 cm
Time taken to cover the distance from A to B =(5 -2) =3s

(ii) The speed of the body as it moves from B to C is zero.
(iii) The distance covered from C to D is (7-3)=4 cm
Time taken to cover the distance from C to D = (9-7)=2s

Question 54:
What can you say about the motion of a body if:
(a) its displacement-time graph is a straight line ?
(b) its velocity-time graph is a straight line ?
Solution :
(a) The body has a uniform velocity if its displacement-time graph is a straight line.
(b) The body has a uniform acceleration if its velocity-time graph is a straight line.
Question 55:
A body with an initial velocity x moves with a uniform acceleration y. Plot its velocity-time graph.
Solution :

Question 56:
Given alongside is the velocity-time graph for a moving body :
Find :
(i) Velocity of the body at point C.
(ii) Acceleration acting on the body between A and
(iii) Acceleration acting on the body between B and C.

Solution :
(i) BC represents uniform velocity. From graph, we see that the velocity of the body at point C = 40km/h
(ii) Acceleration between A and B = slope of line AB
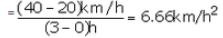
(iii) BC represents uniform velocity, so acceleration acting on the body between B and C is zero.
Question 57:
A body is moving uniformly in a straight line with a velocity of 5 m/s. Find graphically the distance covered by it in 5 seconds.
Solution :
Distance travelled = Area of rectangle OABC
= OA x OC
= 5 x 5 =25 m

Question 58:
The speed-time graph of an ascending passenger lift is given alongside.
What is the acceleration of the lift:
(i) during the first two seconds ?
(ii) between second and tenth second ?
(iii) during the last two seconds ?
Solution:
(i) Acceleration during first two seconds 
(ii) Acceleration between second and tenth second is zero, since the velocity is constant during this time.
(iii) Acceleration during last two seconds 
Question 59:
A car is moving on a straight road with uniform acceleration. The speed of the car varies with time as follows :

Draw the speed-time graph by choosing a convenient scale. From this graph :

(i) Calculate the acceleration of the car.
(ii) Calculate the distance travelled by the car in 10 seconds.
Solution :

(i) Acceleration of the car = slope of line AB 
(ii) Distance travelled by the car in 10 s = area of trapezium OABC

Question 60:
The graph given alongside shows how the speed of a car changes with time:

(i) What is the initial speed of the car ?
(ii) What is the maximum speed attained by the car ?
(iii) Which part of the graph shows zero acceleration ?
(iv) Which part of the graph shows varying retardation ?
(v) Find the distance travelled in first 8 hours.
Solution :
(i) Initial speed of the car=10km/h
(ii) Maximum speed attained by the car= 35km/h
(iii) BC represents zero acceleration.
(iv) CD represents varying retardation.
(v)

Distance travelled in first 8 hrs:
s= Area of trapezium OABF + Area of rectangle BCEF

Question 61:
Three speed-time graphs are given below :



Which graph represents the case of:
(i) a cricket ball thrown vertically upwards and returning to the hands of the thrower ?
(ii) a trolley decelerating to a constant speed and then accelerating uniformly ?
Solution :
(i) Graph (c): The speedof the ball goes on decreasing uniformly as it moves upward, reaches zero at the highest point, and then increases uniformly as it moves downward.
(ii) Grap(a): The speed of the trolley decreases uniformly, then it moves at a constant speed, and then the speed increases uniformly.
Page No:44
Question 62:
Study the speed-time graph of a car given alongside and answer the following questions:

(i) What type of motion is represented by OA ?
(ii) What type of motion is represented by AB ?
(iii) What type of motion is represented by BC ?
(iv) What is the acceleration of car from O to A ?
(v)What is the acceleration of car from A to B ?
(vi) What is the retardation of car from B to C ?
Solution :
(i) OA represents uniform acceleration
(ii) AB represents constant speed.
(iii) BC represents uniform retardation.
(iv) Acceleration of car from O to A = slope of line OA
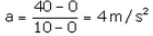
(v) Acceleration of car from A to B is zero as it has uniform speed during this time.
(vi) Retardation of car from B to C = slope of line BC

Question 63:
What type of motion is represented by each one of the following graphs ?




Solution :
(i) Graph (a) represents uniform acceleration.
(ii) Graph (b) represents constant speed.
(iii) Graph (c) represents uniform retardation.
(iv) Graph (d) represents non-uniform retardation.
Question 64:
A car is travelling along the road at 8 ms-1. It accelerates at 1 ms-2 for a distance of 18 m. How fast is it then travelling ?
Solution :
Initial velocity, u=8m/s
Acceleration, a=1m/s2
Distance, s=18m

Question 65:
A car is travelling at 20 m/s along a road. A child runs out into the road 50 m ahead and the car driver steps on the brake pedal. What must the car’s deceleration be if the car is to stop just before it reaches the child ?
Solution :
Initial velocity, u=20m/s
Final velocity, v=0m/s
Distance, s=50m

|
88 videos|369 docs|67 tests
|
FAQs on Lakhmir Singh & Manjit Kaur: Motion, Solutions- 4 - Science Class 9
| 1. What is motion in physics? |  |
| 2. What are the different types of motion? |  |
| 3. How is speed different from velocity? |  |
| 4. What is the difference between distance and displacement? |  |
| 5. How does acceleration affect motion? |  |

|
Explore Courses for Class 9 exam
|

|

















