Equilibrium in Chemical Processes: Dynamic Equilibrium, Law of Chemical Equilibrium | Chemistry for JEE Main & Advanced PDF Download
Equilibrium in Chemical Processes
Chemical reactions, like physical systems, reach a balance known as equilibrium. These reactions can go in two directions: forward and backward.
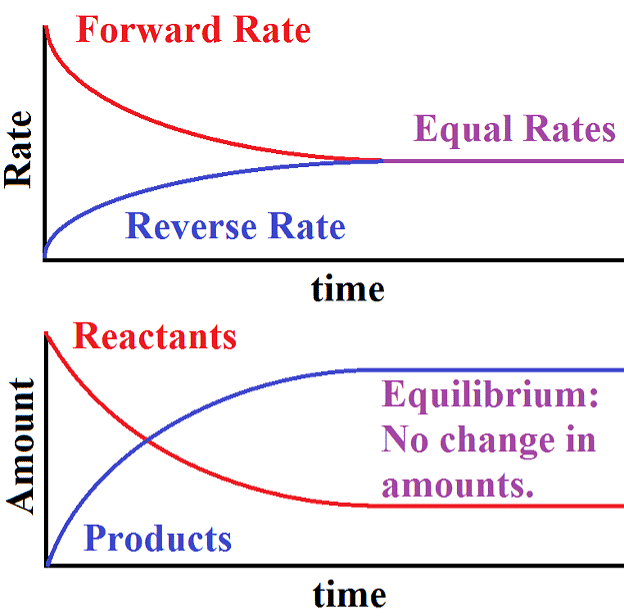
- When the rates of both directions are equal, the concentrations of the starting materials and the resulting products stop changing. This stable situation is called chemical equilibrium.
- It's dynamic because it involves an ongoing process where the forward reaction transforms reactants into products, and the reverse reaction turns products back into the original reactants.
What is Dynamic Equilibrium?
Dynamic Equilibrium can be defined as the state of a given system in which the reversible reaction taking place in it stops changing the ratio of reactants and products, but there is still a movement of substances between the reactants and the products.

- This movement occurs at an equal rate and there is no net change of the reactant and product ratio.
- For these types of equilibria, the equilibrium constants are represented with the help of the rate constants for the forward and backward reactions. Systems maintaining a dynamic equilibrium are examples of systems in steady states.
[Question: 961445]
Dynamic Equilibrium in Haber's Process
In the process of making ammonia using Haber’s method, the dynamic nature of chemical equilibrium is evident. Initially, known amounts of nitrogen (N2) and hydrogen (H2) are combined at high temperatures and pressure. Over time, the amounts of ammonia (NH3), unreacted hydrogen, and nitrogen are measured at regular intervals.
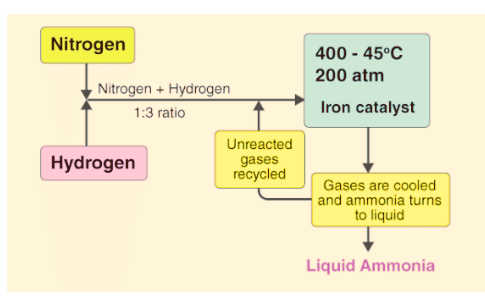
- After a while, a specific composition is reached where the mixture remains constant, indicating equilibrium.
- To understand the dynamic aspect, the synthesis is repeated using deuterium (D2) instead of hydrogen. The equilibrium is achieved with the same composition but with deuterium-containing compounds.
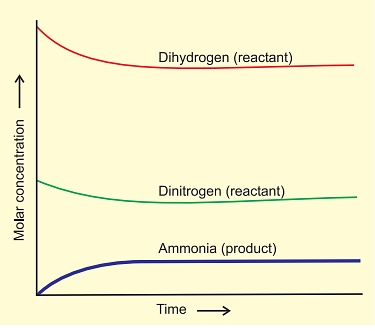 Attainment of Chemical Equilibrium
Attainment of Chemical Equilibrium
- In an intriguing experiment, mixtures from both reactions (H2, N2, NH3, and D2, N2, ND3) are combined. Despite the initial equilibrium composition, further analysis using a mass spectrometer shows a mix of ammonia and its deuterated forms, along with hydrogen and its deuterated forms.
- This reveals that H and D atoms continue to rearrange within the molecules due to ongoing forward and reverse reactions.
- The use of deuterium highlights that chemical reactions reach dynamic equilibrium, where the rates of forward and reverse reactions are balanced, resulting in no net change in composition.
- Equilibrium can be achieved whether starting with H2 and N2 to produce NH3 or starting with NH3 and decomposing it back into N2 and H2.
The balanced chemical equations for the reactions are:
N2 (g) + 3H2 (g) ⇌ 2NH3 (g)
2NH3 (g) ⇌ N2 (g) + 3H2 (g)
[Question: 1236635]
Difference Between Static and Dynamic Equilibrium
- Static equilibrium refers to a condition where the reaction occurring in a system is completely halted and there exists no movement between the reactants and the products corresponding to the chemical reaction.
- If the forces acting on an object cancel each other, in addition to the constancy of content and composition, no movement of the object takes place. This is static equilibrium.

However, the resultant force acting on both of these types of equilibria in a system is zero. Generally, neither of these types of equilibrium display visible changes.
[Question: 1236636]
Equilibrium constant
Let us consider a general reversible reaction,
aA + bB  cC + dD
cC + dD
Based on their experiments with many reversible reactions, Norwegian chemists Cato Maximillian Guldberg and Peter Waage suggested in 1864 that the concentrations in a mixture at equilibrium are connected by the following equilibrium equation.
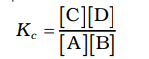
The symbol Kc represents the equilibrium constant, and the formula on the right side is called the equilibrium constant expression.
The equilibrium equation is referred to as the law of mass action because, in the earlier days of chemistry, concentration was termed as "active mass."
Law of Chemical Equilibrium
At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their stoichiometric coefficients has a constant value. This is known as the equilibrium Law or Law of Chemical Equilibrium.
The equilibrium constant (Kc) for a general reaction, where substances A and B react to produce C and D, is given by the formula:
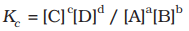
In simpler terms, you calculate it by taking the concentrations of C and D, each raised to their respective coefficients, and then dividing that by the product of the concentrations of A and B, each raised to their respective coefficients.
aA + bB -> cC + dD
Characteristics of the Equilibrium Constant
1. After reversing the reaction the equilibrium constant get reversed.


After reversing the reaction


2. When the two reactions are added their equilibrium constants get multiplied.

 Upon adding the above reactions,
Upon adding the above reactions,
A + B + E + F  C + D + G K3
C + D + G K3
 → K3 = K1 × K2
→ K3 = K1 × K2
3. When the reaction is multiplied by any number then eq. constant gets the same number in its power.


After multiplying by n
nA + nB  nC + nD (K2)
nC + nD (K2)

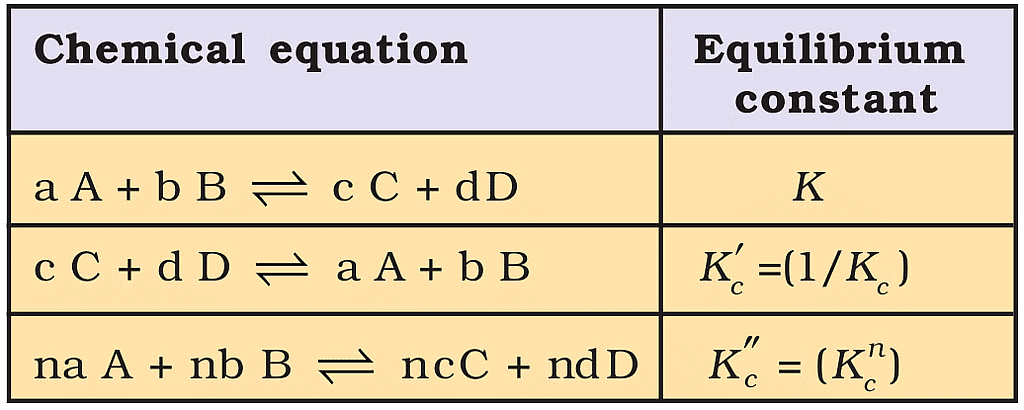 Relations between Equilibrium Constants for a General Reaction and its Multiples.
Relations between Equilibrium Constants for a General Reaction and its Multiples.
Ex. Given the following equilibrium constants:
(1) CaCO3(s) → Ca2+ (aq) + CO32-(aq) K1=10-8.4
(2) HCO3-(aq) → H+ (aq) + CO32-(aq) K2=10-10.3
Calculate the value of K for the reaction CaCO3(s) + H (aq)=Ca2 (aq) + HCO3-(aq)
Sol. The net reaction is the sum of reaction 1 and the reverse of reaction 2:
CaCO3(s) → Ca2 (aq) +CO32-(aq) K1=10-8.4
H+ (aq) + CO32-(aq)→ HCO3-(aq) K-2=10-(-10.3)
-------------------------------------------------
CaCO3(s) + H+ (aq) → Ca2 (aq) + HCO3-(aq),
K=K1/K2=10(-8.4 +10.3) =10+1.9
Note:
- This net reaction describes the dissolution of limestone by acid; it is responsible for the eroding effect of acid rain on buildings and statues.
- This is an example of a reaction that has practically no tendency to take place by itself (the dissolution of calcium carbonate) begin "driven" by a second reaction having a large equilibrium constant.
- From the standpoint of the LeChâtelier principle, the first reaction is "pulled to the right" by the removal of carbonate by the hydrogen ion. "Coupled" reactions of this type are widely encountered in all areas of chemistry, and especially in biochemistry, in which a dozen or so reactions may be linked in this way.
Significance of Equilibrium Constant
(a) Using Keq to Predict Relative Concentrations
The size of the equilibrium constant can give us information about the relative amounts of reactants and products present at equilibrium.
• When K << 1
The reaction lies to the left (mostly reactants)
• When K >> 1
The reaction lies to the right (mostly products)
• When K = 1
The reaction lies in the middle (mix of reactants and products)

(b) Calculating Equilibrium concentrations
Ex. Phosgene is a poisonous gas that dissociates at high temperatures into two other poisonous gases, carbon monoxide and chlorine. The equilibrium constant Kp= 0.0041 atm at 600K. Find the equilibrium composition of the system after 0.124 atm of COCl2 initially is allowed to reach equilibrium at this temperature.
Sol.
| COCl2(g) ⇔ CO(g) + Cl2(g) | ||
initial pressures | 0.124 | 0 | 0 |
change | -x | +x | +x |
equilibrium pressures | 0.124-x | x | x |
Substitution of the equilibrium pressures into the equilibrium expression gives

This expression can be rearranged into standard polynomial form x2 0041x-0.00054=0 and solved by the quadratic formula, but we will simply obtain an approximate solution by iteration.
Because the equilibrium constant is small, we know that x will be rather small compared to 0.124, so the above relation can be approximated by

which gives x=0.025.
To see how good this is, substitute this value of x into the denominator of the original equation and solve again:

This time, solving for x gives 0.0204. Iterating once more, we get

and x = 0.0206 which is sufficiently close to the previous to be considered the final result. The final partial pressures are then 0.104 atm for COCl2, and 0.0206 atm each for CO and Cl2.
Note: using the quadratic formula to find the exact solution yields the two roots -0.0247 (which we ignore) and 0.0206, which show that our approximation is quite good. Note: using the quadraticformula to find the exact solution yields the two roots -0.0247 (which we ignore) and 0.0206, which show that our approximation is quite good.
Reaction Quotient (Q)
At each point in a reaction, we can write a ratio of concentration terms having the same forms as the equilibrium constant expression. The ratio is called the reaction quotient denoted by the symbol Q. It helps in predicting the direction of a reaction.
The expression Q= at any time during the reaction is called the reaction quotient.
at any time during the reaction is called the reaction quotient.
 Reaction Quotient
Reaction Quotient
(i) If Q > KC reaction will proceed in a backward direction until equilibrium is reached.
(ii) If Q < KC reaction will proceed in the forward direction until equilibrium is established.
(iii) If Q = KC reaction is at equilibrium
Ex. For the reaction NOBr (g)  NO(g) + 1/2 Br2(g), Kp=0.15 atm at 90°C. If NOBr, NO, and Br2 are mixed at this temperature having partial pressures 0.5 atm,0.4 atm & 2.0 respectively, will Br2 be consumed or formed?
NO(g) + 1/2 Br2(g), Kp=0.15 atm at 90°C. If NOBr, NO, and Br2 are mixed at this temperature having partial pressures 0.5 atm,0.4 atm & 2.0 respectively, will Br2 be consumed or formed?
Sol. 
KP=0.15
Hence, the reaction will shift in the backward direction. Therefore, Br2 will be consumed.
Degree of Dissociation & Vapour Density
Let us consider the following Reaction:


Here α is the degree of dissociation.
Ex. The Vapour Density of a mixture of PCl5, PCl3, and Cl2 is 92. Find the degree of dissociation of PCl5.
Sol.

1 0 0
1 - x x x
 = 104.25,
= 104.25,
 , α =0.13
, α =0.13
|
352 videos|596 docs|309 tests
|
FAQs on Equilibrium in Chemical Processes: Dynamic Equilibrium, Law of Chemical Equilibrium - Chemistry for JEE Main & Advanced
| 1. What is dynamic equilibrium in chemical processes? |  |
| 2. How is dynamic equilibrium involved in Haber's process? |  |
| 3. What is the difference between static and dynamic equilibrium? |  |
| 4. What is the equilibrium constant in chemical processes? |  |
| 5. What is the law of chemical equilibrium? |  |
|
352 videos|596 docs|309 tests
|

|
Explore Courses for JEE exam
|

|


















