Linear Algebra and Matrices | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
| Table of contents |

|
| Introduction |

|
| Linear Algebra |

|
| Group and Field |

|
| Vector Space |

|
| Basis of a Vector Space |

|
| Linear Transformations |

|
| Kernel and Range of a Linear Transformation |

|
| Matrices and Their Properties |

|
Introduction
Welcome to the world of groups, fields, and vector spaces—the mathematical frameworks that form the backbone of modern physics and mathematics.
Groups, fields, and vector spaces are the building blocks of mathematical physics. They are the key to understanding complex systems, solving differential equations, and tackling real-world problems in mechanics, electromagnetism, and quantum theory.
For IIT JAM students, these concepts aren’t just theoretical—they are the stepping stones to mastering advanced physics and mathematics and exploring the fundamental nature of reality.
Linear Algebra
It plays a fundamental role in various aspects of physics, as demonstrated by the five examples mentioned.
- In the first three examples related to classical physics, we encounter vectors positioned at different points in space and time.
- However, the fifth example presents a vector space where the vectors should not be interpreted as simple arrows in our everyday classical space.
- This highlights the importance of linear algebra as a foundational tool in the study of physics.
- Instead of initially viewing vectors as representations of physical processes, it is more beneficial to approach the topic from a mathematical and abstract perspective.
- By familiarizing ourselves with the techniques involved in linear algebra, we can later apply them to the intuitive concept of vectors as arrows situated at various points in the classical three-dimensional space.
Group and Field
Let X and Y be sets. The Cartesian product X × Y , of X with Y is the set of all possible pairs (x, y ) such that x ∈ X and y ∈ Y .
A group is a non-empty set G, together with an operation, which is a mapping ‘ · ’ : G × G → G, such that the following conditions are satisfied.
1. For all a, b, c ∈ G, we have (a · b) · c = a · (b · c),
2. There exists a particular element (the “neutral” element), often called e in group theory, such that e · g = g · e = g, for all g ∈ G.
3. For each g ∈ G, there exists an inverse element g−1 ∈ G such that g · g−1 = g−1 · g = e.
If, in addition, we have a · b = b · a for all a, b ∈ G, then G is called an “Abelian” group.
A field is a non-empty set F, having two arithmetical operations, denoted by ‘+’ and ‘·’, that is, addition and multiplication.
Under addition, F is an Abelian group with a neutral element denoted by ‘0’. Furthermore, there is another element, denoted by ‘1’, with 1 ≠ 0, such that F \ {0} (that is, the set F, with the single element 0 removed) is an Abelian group, with neutral element 1, under multiplication. In addition, the distributive property holds:
a · (b + c) = a · b + a · c and (a + b) · c = a · c + b · c, for all a, b, c ∈ F .
The simplest example of a field is the set consisting of just two elements {0, 1} with the obvious multiplication. This is the field Z/2Z. Also, as we have seen in the analysis lectures, for any prime number p ∈ N, the set Z/pZ of residues modulo p is a field.
Vector Space
Let (F, +, .) be a field. The elements of F are called scalars. Let V be a non-empty set whose elements are called vectors. Then V is a vector space over the field F (denoted by V(F)) if
Examples
(i) R is a vector space over R denoted by R(R).(ii) C is a vector space over R denoted by C(R).
(iii) Every field is vector space over its subfield.
Vector Subspace
If V(F) is a vector space, then we say W is a subspace of V if W also forms a vector space over the same field F.
Example: The set {0} and V are always subspaces of V.
Linear Combination
 Linear Dependence :
Linear Dependence :
 Linear Independence :
Linear Independence :
Basis of a Vector Space
A subset S of a vector space V(F) is called a basis of V(F) if it meets the following conditions:
(i) The set S contains linearly independent vectors.
(ii) The set S generates the vector space V(F), meaning every vector in V can be expressed as a linear combination of a finite number of vectors from S.
Example: If V is R3, the standard basis b is given by the vectors (1, 0, 0), (0, 1, 0), and (0, 0, 1).
Dimension of a Vector Space: For a vector space V(F) over F with a basis b, the number of vectors in b represents the dimension of the vector space.
Linear Transformations
Let's say we have two vector spaces, U(F) and V(F), both over the same field F.
A mapping T : U → V is called a homomorphism or a linear transformation from U to V if it satisfies the following condition:
T(au + bv) = aT(u) + bT(v)
for all u, v ∈ U and a, b ∈ F.
This means that T preserves the linear structure of the vector space U when mapping it to the vector space V.
Kernel and Range of a Linear Transformation
Kernel of Linear Transformation
Consider a linear transformation T: V → V'. The kernel of T, denoted as ker(T), is the set of all vectors x in V such that T(x) = 0. In other words, it is the set of vectors that are mapped to the zero vector in V' by the transformation T. Mathematically, the kernel is defined as:
ker(T) = { x ∈ V | T(x) = 0 }
The kernel represents the "input" vectors that are collapsed to the zero vector in the output space.
Range of Linear Transformation
The range of a linear transformation T: V(F) → V'(F) is the set of all vectors in V' that can be obtained by applying the transformation T to vectors in V. It is denoted as R(T) and is defined as:
R(T) = { T(x) | x ∈ V }
The range represents the set of all possible outputs that can be produced by the transformation T from the input space V.
Matrices and Their Properties
A matrix is a collection of m n numbers arranged in a rectangular format. It consists of m rows and n columns, and is referred to as an m × n matrix or a matrix of order m × n. It is typically denoted as A = [aij] m×n.
Trace of a Square Matrix
The trace of a square matrix A is the sum of all its diagonal elements. This means that if you take the elements that run from the top left to the bottom right of the matrix, their total is known as the trace.
Example:
Transpose of a matrix
If A = [aij] with dimensions m × n, then the transpose of A, which is written as AT, is defined as AT = [bij] with dimensions n × m.
Example: 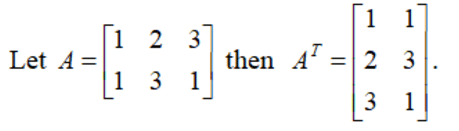
Adjoint of a square matrix
If A is a square matrix represented as A = [aij] of size n x n, then the cofactor matrix B is defined as B = [Aij], where Aij is the cofactor of the element aij in the determinant |A|.
- The transpose of the cofactor matrix B is called the adjoint of matrix A.
- This is denoted as Adj A = [Aij] of size n x n.
- Inverse of A:
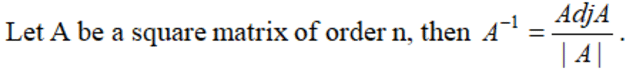
Example: 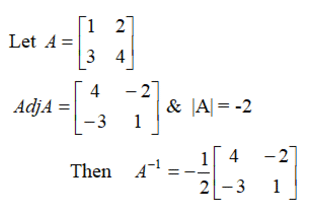
Eigen value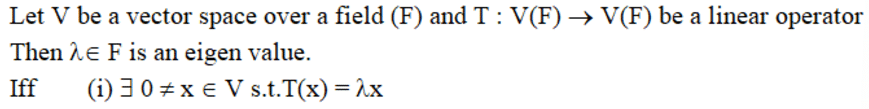
Eigen Vector 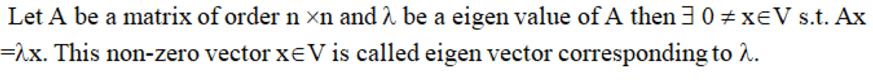
Characteristic polynomial
Let A be square matrix of order n then CA(x) = |A – xI| is a polynomial of degree n called the characteristic polynomial of A.
Minimal polynomial
The monic polynomial of lowest degree that annihilates a matrix A is called the minimal polynomial of A. It is denoted by m(x).
Also if f(x) is the minimal polynomial of A, the equation f(x) = 0 is called the minimal equation of the matrix A.
FAQs on Linear Algebra and Matrices - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the definition of a vector space? |  |
| 2. How do you find a basis for a vector space? |  |
| 3. What are the kernel and range of a linear transformation? |  |
| 4. What is the relationship between matrices and linear transformations? |  |
| 5. What properties do matrices have that are important in linear algebra? |  |






















