Linear Equations in Two Variables | Mathematics for ACT PDF Download
A linear equation in two variables is an equation in which two variables have the exponent 1. A system of equations with two variables has a unique solution, no solutions, or infinitely many solutions. A linear system of equations may have 'n' number of variables. An important thing to keep in mind while solving linear equations with n number of variables is that there must be n equations to solve and determine the value of variables.
The set of solutions obtained by solving these linear equations is a straight line. Linear equations in two variables are the algebraic equations which are of the form (or can be converted to the form) y = mx + b, where m is the slope and b is the y-intercept. They are the equations of the first order. For example, y = 2x + 3 and 2y = 4x + 9 are two-variable linear equations.
What are Linear Equations in Two Variables?
The linear equations in two variables are the equations in which each of the two variables are of the highest exponent order of 1 and have one, none, or infinitely many solutions. The standard form of a two-variable linear equation is ax + by + c = 0 where x and y are the two variables. The solutions can also be written in ordered pairs like (x, y). The graphical representation of the system of linear equations in two variables includes two straight lines which could be intersecting lines, parallel lines, or coincident lines.

Forms of Linear Equations in Two Variables
A linear equation in two variables can be in different forms like standard form, intercept form and point-slope form. For example, the same equation 2x + 3y = 9 can be represented in each of the forms like 2x + 3y - 9 = 0 (standard form), y = (-2/3)x + 3 (slope-intercept form), and y - 5/3 = -2/3(x + (-2)) (point-slope form). Look at the image given below showing all these three forms of representing linear equations in two variables with examples.
The system of equations means the collection of equations and they are referred to as simultaneous linear equations. We will learn how to solve linear equations in two variables using different methods.
Methods of Solving Linear Equations in Two Variables
There are five methods to solve a system of linear equations in two variables. Those methods are explained below
Graphical Method for Solving Linear Equations in Two Variables
The steps to solve linear equations in two variables graphically are given below:
- Step 1: To solve a system of two equations in two variables graphically, we graph each equation.
- Step 2: To graph an equation manually, first convert it to the form y=mx+b by solving the equation for y.
- Step 3: Start putting the values of x as 0, 1, 2, and so on and find the corresponding values of y, or vice-versa.
- Step 4: Identify the point where both lines meet.
- Step 5: The point of intersection is the solution of the given system.

Example: Find the solution of the following system of equations graphically.
-x + 2y - 3 = 0
3x + 4y - 11= 0
Solution: We will graph them and see whether they intersect at a point. As you can see below, both lines meet at (1, 2).
Thus, the solution of the given system of linear equations is x = 1 and y = 2.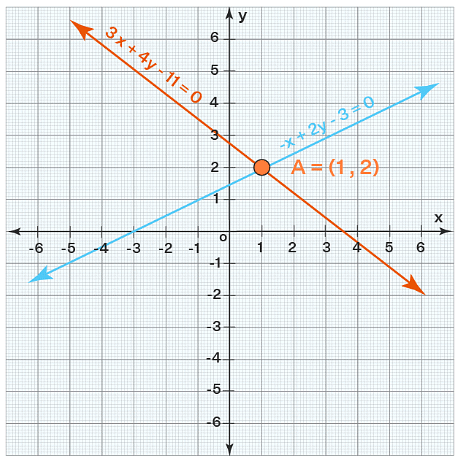
But both lines may not intersect always. Sometimes they may be parallel. In that case, the system of linear equations in two variables has no solution. In some other cases, both lines coincide with each other. In that case, each point on that line is a solution of the given system and hence the given system has an infinite number of solutions.
Consistent and Inconsistent System of Linear Equations:
- If the system has a solution, then it is said to be consistent;
- otherwise, it is said to be inconsistent.
Independent and Dependent System of Linear Equations:
- If the system has a unique solution, then it is independent.
- If it has an infinite number of solutions, then it is dependent. It means that one variable depends on the other.
Consider a system of two linear equations: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0. Here we can understand when a linear system with two variables is consistent/inconsistent and independent/dependent.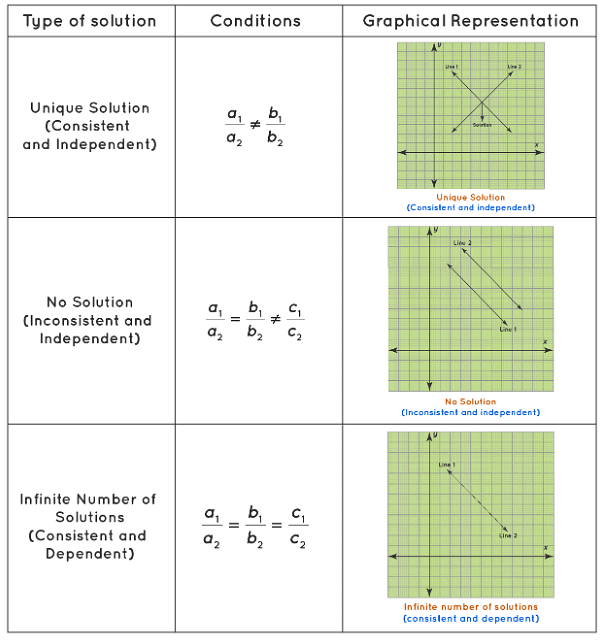
Method of Substitution
To solve a system of two linear equations in two variables using the substitution method, we have to use the steps given below:
- Step 1: Solve one of the equations for one variable.
- Step 2: Substitute this in the other equation to get an equation in terms of a single variable.
- Step 3: Solve it for the variable.
- Step 4: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the substitution method.
x + 2y-7 = 0
2x - 5y + 13 = 0
Solution: Let us solve the equation, x + 2y - 7 = 0 for y:
x + 2y - 7 = 0
⇒2y = 7 - x
⇒ y=(7 - x)/2
Substitute this in the equation, 2x - 5y + 13 = 0:
2x - 5y + 13 = 0
⇒ 2x - 5((7-x)/2) + 13 = 0
⇒ 2x - (35/2) + (5x/2) + 13 = 0
⇒ 2x + (5x/2) = 35/2 - 13
⇒ 9x/2 = 9/2
⇒ x=1
Substitute x=1 this in the equation y = (7-x)/2:
y=(7 - 1)/2 = 3
Therefore, the solution of the given system is x = 1 and y = 3.
Equation 1: 3x - y = 7
Equation 2: 2x + 3y = 12
Cross Multiplication Method
Consider a system of linear equations: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
To solve this using the cross multiplication method, we first write the coefficients of each of x and y and constants as follows:
Here, the arrows indicate that those coefficients have to be multiplied. Now we write the following equation by cross multiplying and subtracting the products.
From this equation, we get two equations:
Solving each of these for x and y, the solution of the given system is:
Method of Elimination
To solve a system of linear equations in two variables using the elimination method, we will use the steps given below:
- Step 1: Arrange the equations in the standard form: ax + by + c = 0 or ax + by=c.
- Step 2: Check if adding or subtracting the equations would result in the cancellation of a variable.
- Step 3: If not, multiply one or both equations by either the coefficient of x or y such that their addition or subtraction would result in the cancellation of any one of the variables.
- Step 4: Solve the resulting single variable equation.
- Step 5: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the elimination method.
2x + 3y -11= 0
3x + 2y - 9 = 0
Adding or subtracting these two equations would not result in the cancellation of any variable. Let us aim at the cancellation of x. The coefficients of x in both equations are 2 and 3. Their LCM is 6. We will make the coefficients of x in both equations 6 and -6 such that the x terms get canceled when we add the equations.
3 × (2x + 3y - 11 = 0)
⇒ 6x + 9y - 33 = 0
-2 × (3x + 2y - 9 = 0)
⇒ -6x - 4y + 18 = 0
Now we will add these two equations:
6x + 9y - 33 = 0
-6x - 4y + 18 = 0
On adding both the above equations we get,
⇒ 5y - 15 = 0
⇒ 5y = 15
⇒ y = 3
Substitute this in one of the given two equations and solve the resultant variable for x.
2x + 3y - 11 = 0
⇒ 2x + 3(3) - 11 = 0
⇒ 2x + 9 - 11 = 0
⇒ 2x = 2
⇒ x = 1
Therefore, the solution of the given system of equations is x = 1 and y = 3.
Equation 1: 4x - 2y = 10 Equation 2: 3x + y = 5 Which of the following choices presents the correct values of 'x' and 'y' that satisfy the system of equations?
Determinant Method
The determinant of a 2 × 2 matrix is obtained by cross multiplying elements starting from the top left corner and subtracting the products.
Consider a system of linear equations in two variables: a1x + b1y = c1 and a2x + b2y = c2. To solve them using the determinants method (which is also known as Crammer's Rule), follow the steps given below:
- Step 1: We first find the determinant formed by the coefficients of x and y and label it Δ.

- Step 2: Then we find the determinant Δx which is obtained by replacing the first column of Δ with constants.

- Step 3: We then find the determinant Δy which is obtained by replacing the second column of Δ with constants.

Now, the solution of the given system of linear equations is obtained by the formulas:
x = Δx / Δ
y = Δy / Δ
Tricks and Tips on Linear Equations with Two Variables:
While solving the equations using either the substitution method or the elimination method:
- If we get an equation that is true (i.e., something like 0 = 0, -1 = -1, etc), then it means that the system has an infinite number of solutions.
- If we get an equation that is false (i.e., something like 0 = 2, 3 = -1, etc), then it means that the system has no solution.
Linear Equations in Two Variables Examples
Example 1: The sum of the digits of a two-digit number is 8. When the digits are reversed, the number is increased by 18. Find the number.
Solution: Let us assume that x and y are the tens digit and the ones digit of the required number. Then the number is 10x+y. And the number when the digits are reversed is 10y + x.
The question says, "The sum of the digits of a two-digit number is 8".
So from this, we get a linear equation in two variables: x + y = 8. ⇒ y = 8 - x
Also, when the digits are reversed, the number is increased by 18.
So, the equation is 10y + x =10x + y + 18
⇒ 10(8 - x) + x =10x + (8 - x) +18 (by substituting the value of y)
⇒ 80 - 10x + x =10x + 8 - x + 18
⇒ 80 - 9x = 9x + 26
⇒ 18x = 54
⇒ x = 3
Substituting x=3 in y = 8 - x, we get,
⇒ y = 8 - 3 = 5
⇒ 10x + y = 10(3) + 5 = 35
Example 2: Jake's piggy bank has 11 coins (only quarters or dimes) that have a total value of $1.85. How many dimes and quarters does the piggy bank has?
Solution: Let us assume that the number of dimes be x and the number of quarters be y in the piggy bank. Let us form linear equations in two variables based on the given information.
Since there are 11 coins in total, x+y=11 ⇒ y=11-x.
We know that, 1 dime = 10 cents and 1 quarter = 25 cents.
The total value of the money in the piggy bank is $1.85 (185 cents).
Thus we get the equation 10x + 25y = 185
⇒ 10x + 25(11 - x) = 185 (as y = 11-x)
⇒ 10x + 275 - 25x =185
⇒ -15x +275 =185
⇒ -15x = -90
⇒ x = 6
Substitute this value of x in x + y =11.
⇒ y = 11 - 6 = 5
|
144 videos|100 docs|61 tests
|
FAQs on Linear Equations in Two Variables - Mathematics for ACT
| 1. What is a linear equation in two variables? |  |
| 2. How do you graph a linear equation in two variables? |  |
| 3. What are the different forms of linear equations in two variables? |  |
| 4. How do you find the slope of a linear equation? |  |
| 5. What is the significance of the y-intercept in a linear equation? |  |

|
Explore Courses for ACT exam
|

|























