Linear Search & Binary Search- 2 | Algorithms - Computer Science Engineering (CSE) PDF Download
Binary Search
Given a sorted array arr[] of n elements, write a function to search a given element x in arr[].
A simple approach is to do a linear search. The time complexity of the above algorithm is O(n). Another approach to perform the same task is using Binary Search.
Binary Search: Search a sorted array by repeatedly dividing the search interval in half. Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise, narrow it to the upper half. Repeatedly check until the value is found or the interval is empty.
Example :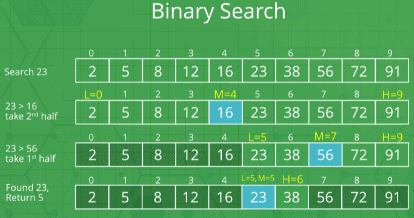 The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
We basically ignore half of the elements just after one comparison.
- Compare x with the middle element.
- If x matches with the middle element, we return the mid index.
- Else If x is greater than the mid element, then x can only lie in the right half subarray after the mid element. So we recur for the right half.
- Else (x is smaller) recur for the left half.
Recursive implementation of Binary Search
- C++
// C++ program to implement recursive Binary Search
#include <bits/stdc++.h>
using namespace std;
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not
// present in array
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
int result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
} - C
// C program to implement recursive Binary Search
#include <stdio.h>
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not
// present in array
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? printf("Element is not present in array")
: printf("Element is present at index %d",
result);
return 0;
} - Java
// Java implementation of recursive Binary Search
class BinarySearch {
// Returns index of x if it is present in arr[l..
// r], else return -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the
// middle itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not present
// in array
return -1;
}
// Driver method to test above
public static void main(String args[])
{
BinarySearch ob = new BinarySearch();
int arr[] = { 2, 3, 4, 10, 40 };
int n = arr.length;
int x = 10;
int result = ob.binarySearch(arr, 0, n - 1, x);
if (result == -1)
System.out.println("Element not present");
else
System.out.println("Element found at index " + result);
}
}
/* This code is contributed by Rajat Mishra */ - Python3
# Python3 Program for recursive binary search.
# Returns index of x in arr if present, else -1
def binarySearch (arr, l, r, x):
# Check base case
if r >= l:
mid = l + (r - l) // 2
# If element is present at the middle itself
if arr[mid] == x:
return mid
# If element is smaller than mid, then it
# can only be present in left subarray
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# Else the element can only be present
# in right subarray
else:
return binarySearch(arr, mid + 1, r, x)
else:
# Element is not present in the array
return -1
# Driver Code
arr = [ 2, 3, 4, 10, 40 ]
x = 10
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print ("Element is present at index % d" % result)
else:
print ("Element is not present in array") - C#
// C# implementation of recursive Binary Search
using System;
class GFG {
// Returns index of x if it is present in
// arr[l..r], else return -1
static int binarySearch(int[] arr, int l,
int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the
// middle itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not present
// in array
return -1;
}
// Driver method to test above
public static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int n = arr.Length;
int x = 10;
int result = binarySearch(arr, 0, n - 1, x);
if (result == -1)
Console.WriteLine("Element not present");
else
Console.WriteLine("Element found at index "
+ result);
}
}
// This code is contributed by Sam007. - PHP
<?php
// PHP program to implement
// recursive Binary Search
// A recursive binary search
// function. It returns location
// of x in given array arr[l..r]
// is present, otherwise -1
function binarySearch($arr, $l, $r, $x)
{
if ($r >= $l)
{
$mid = ceil($l + ($r - $l) / 2);
// If the element is present
// at the middle itself
if ($arr[$mid] == $x)
return floor($mid);
// If element is smaller than
// mid, then it can only be
// present in left subarray
if ($arr[$mid] > $x)
return binarySearch($arr, $l,
$mid - 1, $x);
// Else the element can only
// be present in right subarray
return binarySearch($arr, $mid + 1,
$r, $x);
}
// We reach here when element
// is not present in array
return -1;
}
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$n = count($arr);
$x = 10;
$result = binarySearch($arr, 0, $n - 1, $x);
if(($result == -1))
echo "Element is not present in array";
else
echo "Element is present at index ",
$result;
// This code is contributed by anuj_67.
?> - Javascript
<script>
// JavaScript program to implement recursive Binary Search
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
function binarySearch(arr, l, r, x){
if (r >= l) {
let mid = l + Math.floor((r - l) / 2);
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not
// present in array
return -1;
}
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length
let result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? document.write( "Element is not present in array")
: document.write("Element is present at index " +result);
</script>
Output: Element is present at index 3
Here you can create a check function for easier implementation.
Here is recursive implementation with check function which I feel is a much easier
Implementation:
- C++
C++
#include <bits/stdc++.h>
using namespace std;
//define array globally
const int N = 1e6 +4;
int a[N];
int n;//array size
//elememt to be searched in array
int k;
bool check(int dig)
{
//element at dig position in array
int ele=a[dig];
//if k is less than
//element at dig position
//then we need to bring our higher ending to dig
//and then continue further
if(k<=ele)
{
return 1;
}
else
{
return 0;
}
}
void binsrch(int lo,int hi)
{
while(lo<hi)
{
int mid=(lo+hi)/2;
if(check(mid))
{
hi=mid;
}
else
{
lo=mid+1;
}
}
//if a[lo] is k
if(a[lo]==k)
cout<<"Element found at index "<<lo;// 0 based indexing
else
cout<<"Element doesnt exist in array";//element was not in our array
}
int main()
{
cin>>n;
for(int i=0; i<n; i++)
{
cin>>a[i];
}
cin>>k;
//it is being given array is sorted
//if not then we have to sort it
//minimum possible point where our k can be is starting index
//so lo=0
//also k cannot be outside of array so end point
//hi=n
binsrch(0,n);
return 0;
}
|
81 videos|113 docs|34 tests
|
FAQs on Linear Search & Binary Search- 2 - Algorithms - Computer Science Engineering (CSE)
| 1. What is the difference between linear search and binary search? |  |
| 2. Which search algorithm is faster: linear search or binary search? |  |
| 3. Can binary search be applied to an unsorted list? |  |
| 4. What are the advantages of using binary search over linear search? |  |
| 5. In which scenarios is linear search preferred over binary search? |  |
















