Linear and Non-Linear Regression | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
Regression analysis is a statistical methodology concerned with relating a variable of interest, which is called the dependent variable and denoted by the symbol y, to a set of independent variables, which are denoted by the symbols x1, x2, …, xp. The dependent and independent variables are also called response and explanatory variables, respectively. The objective is to build a regression model that will enable us to adequately describe, predict, and control the dependent variable on the basis of the independent variables.
Simple Linear Regression Model
The simple linear regression model is a model with a single explanatory variable x that has a relationship with a response variable y that is a straight line. This simple linear regression model is
y = β0 + β1x + ε ......(1)
where the intercept β0 and the slope β1 are unknown constants and ε is a random error component. The errors are assumed to have mean zero and unknown variance σ2. Additionally, we usually assume that the errors are uncorrelated. This means that the value of one error does not depend on the value of any other error.
It is convenient to view the explanatory variable x as controlled by the data analyst and measured with negligible error, while the response variable y is a random variable. That is, there is a probability distribution for y at each possible value for x. The mean of this distribution is
E(y|x) = β0 +β1x .......(2)
and the variance is
Var(y|x) =Var(β0+β1x+ε) = σ2 ......(3)
Thus, the mean of y is a linear function of x although the variance of y does not depend on the value of x. Furthermore, because the errors are uncorrelated, the response variables are also uncorrelated.
The parameters β0 and β1 are usually called regression coefficients. These coefficients have a simple and often useful interpretation. The slope β1 is the change in the mean of the distribution of y produced by a unit change in x. If the range of data on x includes x = 0, then the intercept β0 is the mean of the distribution of the response variable y when x = 0. If the range of x does not include zero, then β0 has no practical interpretation.
Least-squares estimation of the parameters
The method of least squares is used to estimate β0 and β1. That is, β0 and β1 will be estimated so that the sum of the squares of the differences between the observations yi and the straight line is a minimum. Equation 1 can be written as
yi = β0 + β1xi + εi, i = 1,2,...,n .......(4)
Equation 1 maybe viewed as a population regression model while Equation 4 is a sample regression model, written in terms of the n pairs of data (yi, xi) (i = 1, 2, ..., n). Thus, the least-squares criterion is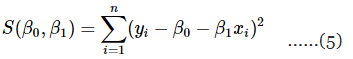
The least-squares estimators of β0 and β1 , say 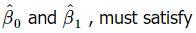
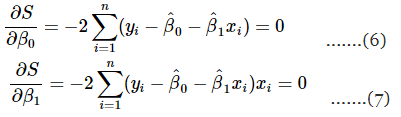
Simplifying these two equations yields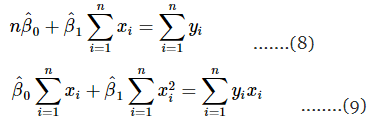
Equations 8 and 9 are called the least-squares normal equations, and the general solution for these simultaneous equations is
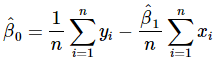 .......(10)
.......(10)
In Equations 10 and 11, 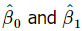 are the least-squares estimators of the intercept and slope, respectively. Thus the fitted simple linear regression model will be
are the least-squares estimators of the intercept and slope, respectively. Thus the fitted simple linear regression model will be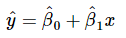 .........(12)
.........(12)
Equation 12 gives a point estimate of the mean of y for a particular x.
Given the averages of yi and xi as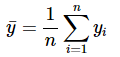 ........(13)
........(13)
and 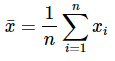 ........(14)
........(14)
the denominator of Equation 11 can be written as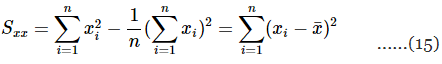
and the numerator of that can be written as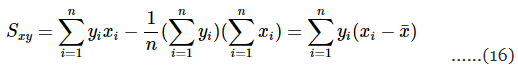
Therefore, Equation 11 can be written in a convenient way as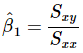 .......(17)
.......(17)
The difference between the observed value yi and the corresponding fitted value 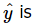 a residual. Mathematically the ith residual is
a residual. Mathematically the ith residual is
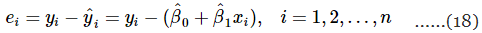
Residuals play an important role in investigating model adequacy and in detecting departures from the underlying assumptions.
Nonlinear Regression
Nonlinear regression is a powerful tool for analyzing scientific data, especially if you need to transform data to fit a linear regression. The objective of nonlinear regression is to fit a model to the data you are analyzing. You will use a program to find the best-fit values of the variables in the model which you can interpret scientifically. However, choosing a model is a scientific decision and should not be based solely on the shape of the graph. The equations that fit the data best are unlikely to correspond to scientifically meaningful models.
Before microcomputers were popular, nonlinear regression was not readily available to most scientists. Instead, they transformed their data to make a linear graph, and then analyzed the transformed data with linear regression. This sort of method will distort the experimental error. Linear regression assumes that the scatter of points around the line follows a Gaussian distribution, and that the standard deviation is the same at every value of x . Also, some transformations may alter the relationship between explanatory variables and response variables. Although it is usually not appropriate to analyze transformed data, it is often helpful to display data after a linear transform, since the human eye and brain evolved to detect edges, but not to detect rectangular hyperbolas or exponential decay curves.
Nonlinear Least-Squares
Given the validity, or approximate validity, of the assumption of independent and identically distributed normal error, one can make certain general statements about the least-squares estimators not only in linear but also in nonlinear regression models. For a linear regression model, the estimates of the parameters are unbiased, are normally distributed, and have the minimum possible variance among a class of estimators known as regular estimators. Nonlinear regression models differ from linear regression models in that the least-squares estimators of their parameters are not unbiased, normally distributed, minimum variance estimators. The estimators achieve this property only asymptotically, that is, as the sample sizes approach infinity.
One-parameter Curves
y = log(x−α) .......(19)
The statistical properties in estimation of this model are good, so the model behaves in a reasonably close-to-linear manner in estimation. An even better-behaved model is obtained by replacing α by an expected-value parameter, to yield
y = log[x−x1+exp(y1)] ........(20)
where y1 is the expected value corresponding to x = x1, where x1 should be chosen to be somewhere within the observed range of the x values in the data set.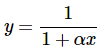 ........(21)
........(21)
When α<0 , there is a vertical asymptote occurring at x=−1/α .
y = exp(x−α) ......(22)
This model is, in fact, a disguised intrinsically linear model, since it may be reparameterized to yield a linear model. That is, replacing α by an expected value parameter y1, corresponding to x = x1, yields
y = y1exp(x−x1) .......(23)
which is clearly linear in the parameter y1.
|
1597 videos|1643 docs|920 tests
|
FAQs on Linear and Non-Linear Regression - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is linear regression? |  |
| 2. What is non-linear regression? |  |
| 3. How is the line of best fit determined in linear regression? |  |
| 4. What are the advantages of linear regression over non-linear regression? |  |
| 5. When should non-linear regression be used instead of linear regression? |  |
















