Logarithms | Mathematics for ACT PDF Download
Introduction
- A logarithm is simply an alternative representation of exponents and proves useful in solving problems beyond the scope of exponentials alone. grasping the concept of logarithms is relatively straightforward. Essentially, understanding logarithms boils down to recognizing that a logarithmic equation is merely an alternative form of an exponential equation.
- Logarithms and exponents are reciprocal concepts, as demonstrated in the following section. Initially introduced by mathematician John Napier to streamline calculations, logarithms swiftly gained traction among scientists, engineers, and others.
Here is the mathematical definition of logs.
Logs Definition
A logarithm is defined using an exponent.
- bx = a ⇔ logb a = x
Here, "log" stands for logarithm. The right side part of the arrow is read to be "Logarithm of a to the base b is equal to x".
A very simple way to remember this is "base stays as the base in both forms" and "base doesn't stay with the exponent in log form". Notice that 'b' is the base both on the left and right sides of the implies symbol and in the log form see that the base b and the exponent x don't stay on the same side of the equation.
Here,
- a and b are two positive real numbers.
- x is a real number.
- a, which is inside the log is called the "argument".
- b, which is at the bottom of the log is called the "base".

The above equation has two things to understand (from the symbol ⇔):
- bx = a ⇒ logb a = x. This is called "exponential to log form"
- logb a = x ⇒ bx = a . This is called "log to exponential form"
Here is a table to understand the conversions from one form to the other form.

Natural Logarithm and Common Logarithm
- Examining the last two rows of the table provided, we encounter loge and log10, which hold particular significance and are bestowed with specific names within logarithmic principles.
- The logarithm with base e, referred to as loge, assumes the title of "natural log." However, it is conventionally denoted by the symbol ln instead of loge.
For instance:
- ex = 2 can be expressed as loge 2 = x or ln 2 = x.
- ex = 7 can be articulated as loge 7 = x or ln 7 = x.
On the other hand, the logarithm with base 10, known as log10, earns the moniker of "common log." Typically, it is simply represented as log without any base specified, which inherently implies a base 10 logarithm.
For example:
- 102 = 100 can be rendered as log10 100 = 2 or log 100 = 2.
- 10-2 = 0.01 can be depicted as log10 0.01 = -2 or log 0.01 = -2.
It's noteworthy that in the examples provided, the base 10 is omitted from the notation as it is implicit.
Rules of Logs
The rules governing logarithms serve to simplify, expand, or consolidate multiple logarithms into a single expression. These rules, or properties, play a fundamental role in logarithmic operations. If one desires a deeper understanding of how these rules are derived, further exploration can be pursued.
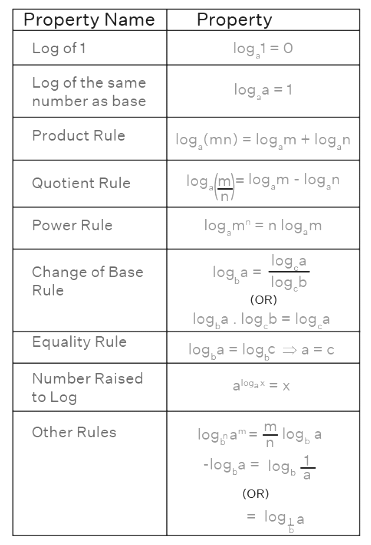
Let's review each of these principles individually.
Log 1
- The value of log 1 irrespective of the base is 0. Because from the properties of exponents, we know that, a0 = 1, for any 'a'. Converting this into log form, loga 1 = 0, for any 'a'. Obviously, when a = 10, log10 1 = 0 (or) simply log 1 = 0.
- When we extend this to the natural logarithm, we have, since e0 = 1 ⇒ ln 1 = 0.
Loga a
Since a1 = a, for any 'a', converting this equation into log form, loga a = 1. Thus, the logarithm of any number to the same base is always 1. For example:
- log2 2 = 1
- log3 3 = 1
- log 10 = 1
- ln e = 1
Product Rule of Log
- The logarithm of a product of two numbers equals the sum of the logarithms of the individual numbers. Symbolically:
- loga (mn) = loga m + loga n
- This mirrors the product rule of exponents: xm ⋅ xn = x(m+n). For example:
- log 6 = log (3 x 2) = log 3 + log 2
- log (5x) = log 5 + log x
Quotient Rule of Log
Similarly, the logarithm of a quotient of two numbers equals the difference between the logarithms of the individual numbers:
- loga (m/n) = loga m - loga n
This aligns with the quotient rule of exponents: xm / xn = x(m-n). For instance:
- log 4 = log (8/2) = log 8 - log 2
- log (x/2) = log x - log 2
Power Rule of Log
The exponent of the argument of a logarithm can be moved to the front of the logarithm:
- loga (mn) = n loga m
This corresponds to the power of power rule of exponents: (xm)^n = x^(mn).
Change of Base Rule
This rule allows changing the base of a logarithm:
- logb a = (log꜀ a) / (log꜀ b)
Alternatively, it can be expressed as logb a · log꜀ b = log꜀ a. This enables changing the base to any desired number, including 10:
- log2 3 = (log 3) / (log 2)
- log3 2 = (log 2) / (log 3)
Equality Rule of Logarithms
This rule is pivotal in solving logarithmic equations:
- logb a = logb c ⇒ a = c
It simplifies equations involving logarithms by canceling out the logarithms from both sides.
Number Raised to Log Property
When a number is raised to a logarithm with the same base as the number, the result equals the argument of the logarithm:
aloga x = x
For example:
2log2 5 = 5
10log 6 = 6
eln 3 = 3
Negative Log Property
Negative logarithms are represented as −logb a. We can calculate this using the power rule of logarithms:
−logb a = logb a-1 = logb (1/a)
Thus,
−logb a = logb (1/a)
In other words, to convert a negative log into a positive log, we can take the reciprocal of the argument or the base:
−logb a = log1/b a
Condensing/Expanding Logarithms
- Logarithms can be either compressed into a single log or expanded into multiple logs using the above rules. The key rules employed in this process include the product rule of logarithms, quotient rule of logarithms, and power rule of logarithms.
Expanding Logarithms:
The logarithm log (3x2y3) can be expanded as:
log (3x2y3)
= log (3) + log (x2) + log (y3) (By product rule)
= log 3 + 2 log x + 3 log y (By power rule)
Condensing Logarithms:
Conversely, the sum of logarithms log 3 + 2 log x + 3 log y can be condensed as:
log 3 + 2 log x + 3 log y
= log (3) + log (x2) + log (y3) (By power rule)
= log (3x2y3) (By product rule)
|
144 videos|104 docs|61 tests
|
FAQs on Logarithms - Mathematics for ACT
| 1. What is the purpose of logarithms in the ACT exam? |  |
| 2. How can logarithms be used to simplify expressions on the ACT exam? |  |
| 3. Are there specific strategies for tackling logarithm questions on the ACT exam? |  |
| 4. What are some common mistakes to avoid when working with logarithms on the ACT exam? |  |
| 5. How can understanding logarithms help in solving real-world problems on the ACT exam? |  |















