Logical Connectives | Engineering Mathematics - Engineering Mathematics PDF Download
Propositions
Before you go through this article, make sure that you have gone through the previous article on
We have discussed
- Proposition is a declarative statement that is either true or false but not both.
- Connectives are used to combine the propositions.
In this article, we will discuss about connectives in propositional logic.
Logical Connectives
Connectives are the operators that are used to combine one or more propositions.
In propositional logic, there are 5 basic connectives: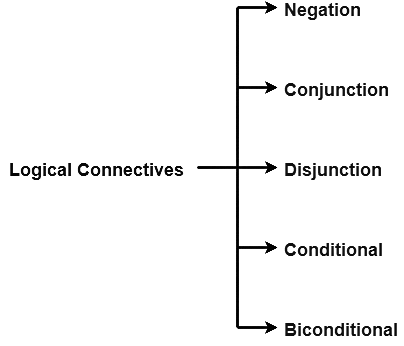

1. Negation
If p is a proposition, then negation of p is a proposition which is-
- True when p is false
- False when p is true.
Truth Table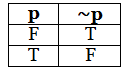
Example
If p : It is raining outside.
Then, Negation of p is-
∼p : It is not raining outside.
2. Conjunction
If p and q are two propositions, then conjunction of p and q is a proposition which is-
- True when both p and q are true
- False when both p and q are false
Truth Table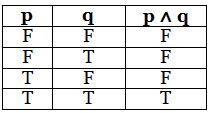
Example
If p and q are two propositions where:
- p : 2 + 4 = 6
- q : It is raining outside.
Then, conjunction of p and q is:
p ∧ q : 2 + 4 = 6 and it is raining outside
3. Disjunction
If p and q are two propositions, then disjunction of p and q is a proposition which is-
- True when either one of p or q or both are true
- False when both p and q are false
Truth Table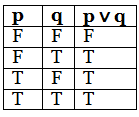
Example
If p and q are two propositions where:
- p : 2 + 4 = 6
- q : It is raining outside
Then, disjunction of p and q is:
p ∨ q : 2 + 4 = 6 or it is raining outside
4. Conditional
If p and q are two propositions, then:
- Proposition of the type “If p then q” is called a conditional or implication proposition.
- It is true when both p and q are true or when p is false.
- It is false when p is true and q is false.
Truth Table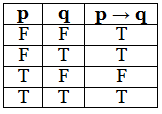
Examples
- If a = b and b = c then a = c.
- If I will go to Australia, then I will earn more money.
5. Biconditional
If p and q are two propositions, then-
- Proposition of the type “p if and only if q” is called a biconditional or bi-implication proposition.
- It is true when either both p and q are true or both p and q are false.
- It is false in all other cases.
Truth Table
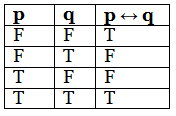
Examples
- He goes to play a match if and only if it does not rain.
- Birds fly if and only if sky is clear.
Important Notes
Note 1:
- Negation ≡ NOT Gate of digital electronics.
- Conjunction ≡ AND Gate of digital electronics.
- Disjunction ≡ OR Gate of digital electronics.
- Biconditional = EX-NOR Gate of digital electronics.
Note 2:
- Each logical connective has some priority.
- This priority order is important while solving questions.
- The decreasing order of priority is-
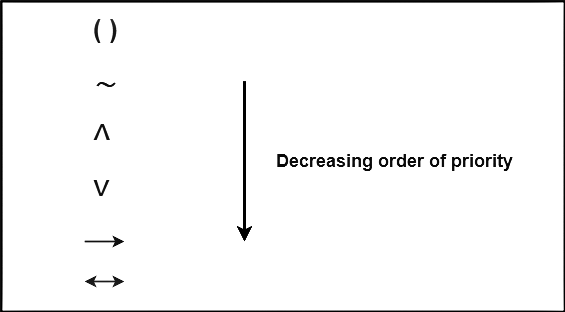
Note 3:
- Negation, Conjunction, Disjunction and Biconditional are both commutative and associative.
- Conditional is neither commutative nor associative.
|
65 videos|129 docs|94 tests
|
FAQs on Logical Connectives - Engineering Mathematics - Engineering Mathematics
| 1. What are the logical connectives used in formal logic? |  |
| 2. How are logical connectives used to form compound statements? |  |
| 3. What is the truth table for the logical connective "or"? |  |
| 4. How does the logical connective "not" work in formal logic? |  |
| 5. What is the difference between implication and biconditional in formal logic? |  |
















