Class 9 Maths Chapter 6 Question Answers - Lines and Angles
Q1: In the adjoining figure, AB || CD. If ∠ APQ = 54° and ∠ PRD = 126°, then find x and y.
Solution: ∵ AB || CD and PQ is a transversal, then interior alternate angles are equal.
⇒ ∠ APQ = ∠ PQR [alt. interior angles]
⇒ 54° = x [∵ ∠ APQ = 54° (Given)]
Again, AB || CD and PR is a transversal, then ∠ APR = ∠ PRD [Interior alternate angles]
But ∠ PRD = 126° [Given]
∴ ∠ APR = 126°
Now, exterior∠ PRD + ∠ PRQ = 180°
⇒ 126°+∠ PRQ = 180°
⇒∠ PRQ= 180°-126° = 54°
In triangle PQR ,
∠ PQR + ∠ PRQ + ∠ QPR = 180° ( Angle sum property)
54°+ 54° +∠ QPR= 180°
108+ ∠ QPR =180°
∠ QPR =180°-108° = 72°
Thus, x = 54° and y = 72°.
Q2: In the adjoining figure AB || CD || EG, find the value of x.
Solution: Let us draw FEG || AB || CD through E.
Now, since FE || AB and BE are transversals,
∴ ∠ ABE + ∠ BEF = 180°
[Interior opposite angles]
⇒ 127° + ∠ BEF = 180° [co int. angles]
⇒ ∠ BEF = 180° - 127° = 53°
Again, EG || CD and CE is a transversal.
∴ ∠ DCE + ∠ CEG = 180° [Interior opposite angles]
⇒ 108° + ∠ CEG = 180° ⇒ ∠ CEG = 180° - 108° = 72°
Since FEG is a straight line, then
⇒ ∠BEF + ∠BEC + ∠CEG = 180° [Sum of angles at a point on the same side of a line = 180°]
⇒ 53° + x + 72° = 180°
⇒ x = 180° - 53° - 72°
= 55°
Thus, the required measure of x = 55°.
Q3: AB and CD are parallel, and EF is a transversal. If ∠BEF = 70°, find ∠EFD and ∠CFE
Ans: Since AB || CD and EF is a transversal, by the Corresponding Angles Theorem:
∠BEF = ∠EFD
Thus, ∠EFD = 70°.
By the Linear Pair Axiom:
∠EFD + ∠CFE = 180°
70° + ∠CFE = 180°
∠CFE = 110°.
So, ∠EFD = 70° and ∠CFE = 110°.
Q4: If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
Ans: 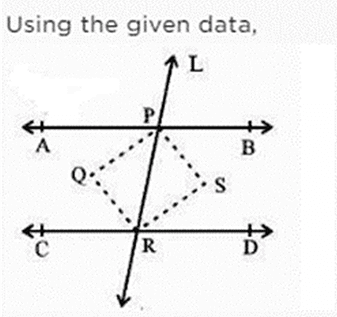
Two parallel lines AB and CD are intersected by a transversal L at P and R
respectively
PQ, RQ, RS and PS are bisectors of ∠APR, ∠PRC, ∠PRD and ∠BPR respectively.
Since AB || CD and L is a transversal
∠APR = ∠PRD ( alt. interior angles)
∠APQ = 1/2(∠PRD) = ∠QPR = ∠PRS
these are alternate interior angles.
QP || RS. Similarly QR || PS.
PQRS is a parallelogram.
Also ray PR stands on AB
∠APR + ∠BPR = 180° ( linear pair)
∠QPR + (1/2) ∠BPR = 90°
∠QPR + ∠SPR = 90°
∠QPS = 90°
Therefore PQRS is a parallelograrn, one of whose angle is 90°.
Hence PQRS satisfies all the properties of being a rectangle.
Hence PQRS is a rectangle
Q5: In the given figure, AOC is a line, find x. 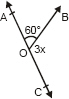
Ans: AOC is a straight line
∠AOB + ∠BOC= 180°
60 + 3x = 180°
3x = 180 - 60
x = 120/ 3
x= 40°
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Question Answers - Lines and Angles
| 1. What are the basic types of angles and their properties? |  |
| 2. How do you find the measure of an unknown angle in a triangle? |  |
| 3. What is the relationship between parallel lines and angles formed by a transversal? |  |
| 4. How can we prove that two lines are parallel using angles? |  |
| 5. What are complementary and supplementary angles, and how can they be identified? |  |

















