Class 9 Maths Chapter 6 Question Answers - Triangles
Q1: In the given figure, AP and DP are bisectors of two adjacent angles A and D of quadrilateral ABCD. Prove that 2 ∠APD = ∠B + 2C.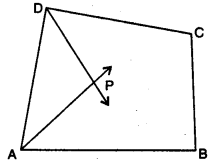 Ans: Here, AP and DP are angle bisectors of ∠A and ∠D
Ans: Here, AP and DP are angle bisectors of ∠A and ∠D
∴ ∠DAP = 1/2∠DAB and ∠ADP = 1/2∠ADC ……(i)
In ∆APD, ∠APD + ∠DAP + ∠ADP = 180°
⇒ ∠APD + 1/2 ∠DAB + 1/2∠ADC = 180°
⇒ ∠APD = 180° – 1/2(∠DAB + ∠ADC)
⇒ 2∠APD = 360° – (∠DAB + ∠ADC) ……(ii)
Also, ∠A + ∠B + C + ∠D = 360°
∠B + ∠C = 360° – (∠A + ∠D)
∠B + ∠C = 360° – (∠DAB + ∠ADC) ……(iii)
From (ii) and (iii), we obtain
2∠APD = ∠B + ∠C
Q2: In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that : (i) ∆AMC ≅ ∆BMD (ii) ∠DBC = 90° (ii) ∆DBC ≅ ∆ACB (iv) CM = 1/2AB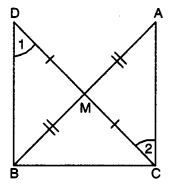 Ans:
Ans:
Given : ∆ACB in which 4C = 90° and M is the mid-point of AB.
To Prove :
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC = 90°
(iii) ∆DBC ≅ ∆ACB
(iv) CM = 1/2AB
Proof : Consider ∆AMC and ∆BMD,
we have AM = BM [given]
CM = DM [given - construction]
∠AMC = ∠BMD [vertically opposite angles]
∴ ∆AMC ≅ ∆BMD [by SAS congruence axiom]
⇒ AC = DB …(i) [by c.p.c.t.]
and ∠1 = ∠2 [by c.p.c.t.]
But ∠1 and ∠2 are alternate angles.
⇒ BD || CA
Now, BD || CA and BC is transversal.
∴ ∠ACB + ∠CBD = 180°
⇒ 90° + CBD = 180°
⇒ ∠CBD = 90°
In ∆DBC and ∆ACB,
we have CB = BC [common]
DB = AC [using (i)]
∠CBD = ∠BCA
∴ ∆DBC ≅ ∆ACB
⇒ DC = AB
⇒ 1/2AB = 1/2DC
⇒ 1/2AB = CM or CM = 1/2AB (∵ CM = 1/2DC)
Q3: Prove that two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle.
Ans:
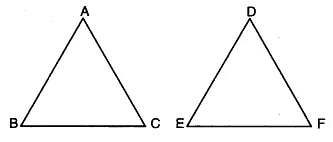
Given : Two As ABC and DEF in which
∠B = ∠E,
∠C = ∠F and BC = EF
To Prove : ∆ABC = ∆DEF
Proof : We have three possibilities
Case I. If AB = DE,
we have AB = DE,
∠B = ∠E and BC = EF.
So, by SAS congruence axiom, we have ∆ABC ≅ ∆DEF
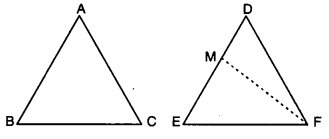
Case II. If AB < ED, then take a point Mon ED
such that EM = AB.
Join MF.
Now, in ∆ABC and ∆MEF,
we have
AB = ME, ∠B = ∠E and BC = EF.
So, by SAS congruence axiom,
we have ΔΑΒC ≅ ΔΜEF
⇒ ∠ACB = ∠MFE
But ∠ACB = ∠DFE
∴ ∠MFE = ∠DFE
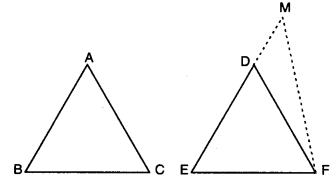
Which is possible only when FM coincides with B FD i.e., M coincides with D.
Thus, AB = DE
∴ In ∆ABC and ∆DEF, we have
AB = DE,
∠B = ∠E and BC = EF
So, by SAS congruence axiom, we have
∆ABC ≅ ∆DEF
Case III. When AB > ED
Take a point M on ED produced
such that EM = AB.
Join MF
Proceeding as in Case II, we can prove that
∆ABC = ∆DEF
Hence, in all cases, we have
∆ABC = ∆DEF.
Q4: In the given figure, side QR is produced to the point S. If the bisectors of ∠PQR and ∠PRS meet at T, prove that ∠QTR = 1/2 ∠QPR.
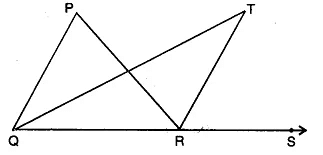
In triangle QTR, ∠TRS is an exterior angle.
:. ∠QTR + ∠TQR = ∠TRS
∠QTR = ∠TRS - ∠TQR ------(1)
For triangle PQR, ∠PRS is an external angle.
:. ∠QPR + ∠PQR = ∠PRS
∠QPR + 2∠TQR = 2∠TRS (As QT and RT are angle bisectors)
∠QPR = 2(∠TRS - ∠TQR)
∠QPR = 2∠QTR [By using equation (1)]
LQTR= 1/2 ∠QPR
Q5: In figure, ABC is an isosceles triangle with AB = AC. D is a point in the interior of ∆ABC such that ∠BCD = ∠CBD. Prove that AD bisects ∠BAC of ∆ABC.
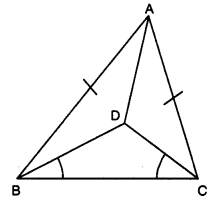
Ans:
In ∆BDC, we have ∠DBC = ∠DCB (given).
⇒ CD = BD (sides opp. to equal ∠s of ∆DBC)
Now, in ∆ABD and ∆ACD,
we have AB = AC [given]
BD = CD [proved above]
AD = AD [common]
∴ By using SSS congruence axiom, we obtain
∆ABD ≅ ∆ACD
⇒ ∠BAD = ∠CAD [c.p.ç.t.]
Hence, AD bisects ∠BAC of ∆ABC.
Q6: In figure, ABCD is a square and EF is parallel to diagonal BD and EM = FM. Prove that (i) DF = BE (ii) AM bisects ∠BAD.
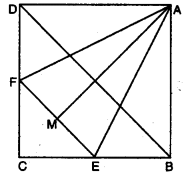
Ans:
(i) EF || BD = ∠1 = ∠2 and ∠3 = ∠4 [corresponding ∠s]
Also, ∠2 = ∠4
⇒ ∠1 = ∠3
⇒ CE = CF (sides opp. to equals ∠s of a ∆]
∴ DF = BE [∵ BC – CE = CD – CF)
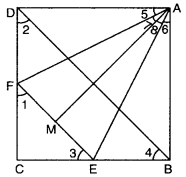
(ii) In ∆ADF and ∆ABE, we have
AD = AB [sides of a square]
DF = BE [proved above]
∠D = ∠B = 90°
⇒ ∆ADF ≅ ∆ABE [by SAS congruence axiom]
⇒ AF = AE and ∠5 = ∠6 … (i) [c.p.c.t.]
In ∆AMF and ∆AME
AF = AE [proved above]
AM = AM [common]
FM = EM (given)
∴ ∆AMF ≅ ∆AME [by SSS congruence axiom]
∴ ∠7 = ∠8 …(ii) [c.p.c.t.]
Adding (i) and (ii), we have
∠5 + ∠7 = ∠6 + ∠8
∠DAM = ∠BAM
∴ AM bisects ∠BAD.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Question Answers - Triangles
| 1. What are the different types of triangles based on their sides? |  |
| 2. How do you calculate the area of a triangle? |  |
| 3. What is the Pythagorean theorem and how does it relate to triangles? |  |
| 4. What are the properties of similar triangles? |  |
| 5. How can you determine if a triangle is a right triangle using side lengths? |  |

















