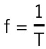Longitudinal & Transverse Waves | Physics for Grade 12 PDF Download
In mechanical waves, particles oscillate about fixed points
- A progressive wave is an oscillation that transfers energy and information
- The substance in which the waves move through are disturbed (eg. water, air)
- The particles of the substance oscillate about a fixed position
- This is sometimes called a travelling wave
- There are two types of waves
- Transverse
- Longitudinal
- The type of wave can be determined by the direction of the oscillations in relation to the direction the wave is travelling
Transverse Waves
- A transverse wave is defined as:
A wave in which the particles oscillate perpendicular to the direction of the wave travel (and energy transfer) - Examples of transverse waves are:
Electromagnetic waves e.g. radio, visible light, UV
Vibrations on a guitar string - Transverse waves can be shown on a rope
- Transverse waves can be polarised
Longitudinal Waves
- A longitudinal wave is defined as:
A wave in which the particles oscillate parallel to the direction of the wave travel (and energy transfer) - Examples of longitudinal waves are:
- Sound waves
- Ultrasound waves
- Longitudinal waves can be shown on a slinky spring
- Longitudinal waves cannot be polarised
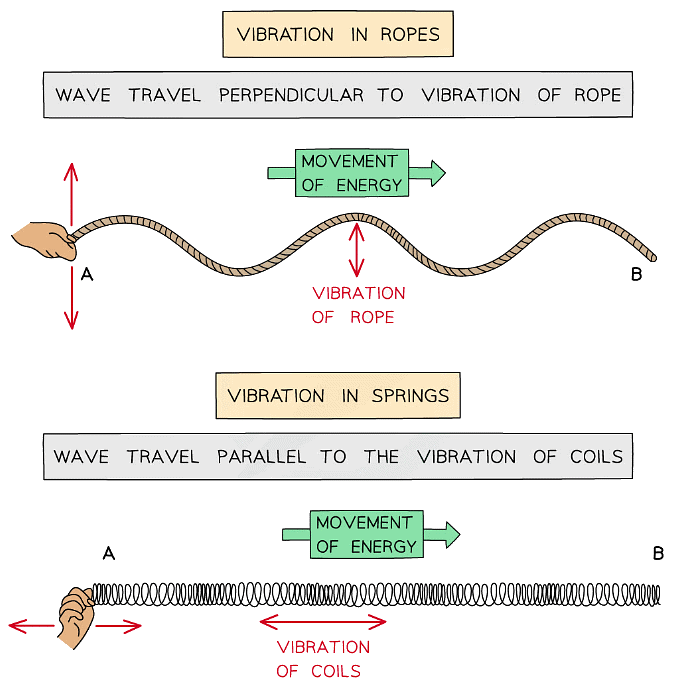 Waves can be shown through vibrations in ropes or springs
Waves can be shown through vibrations in ropes or springs
General Wave Properties
Displacement (x) of a wave is the distance of a point on the wave from its equilibrium position
It is a vector quantity; it can be positive or negative
Amplitude (A) is the maximum displacement of a particle in the wave from its equilibrium position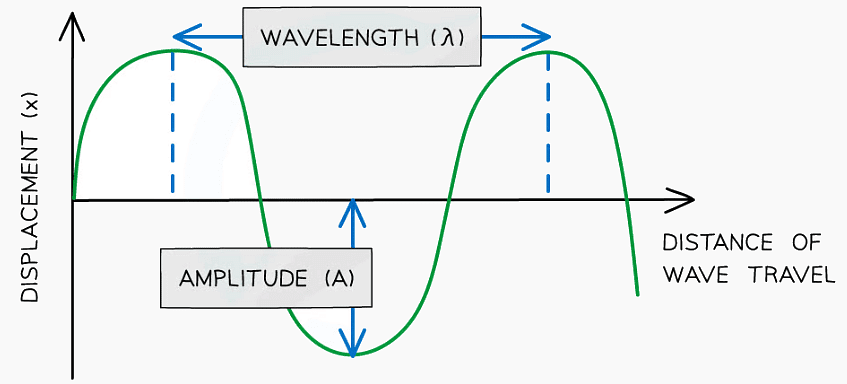 Diagram showing the amplitude and wavelength of a wave
Diagram showing the amplitude and wavelength of a wave
- Wavelength (λ) is the distance between points on successive oscillations of the wave that are in phase
- Displacement, amplitude and wavelength are all measured in metres (m)
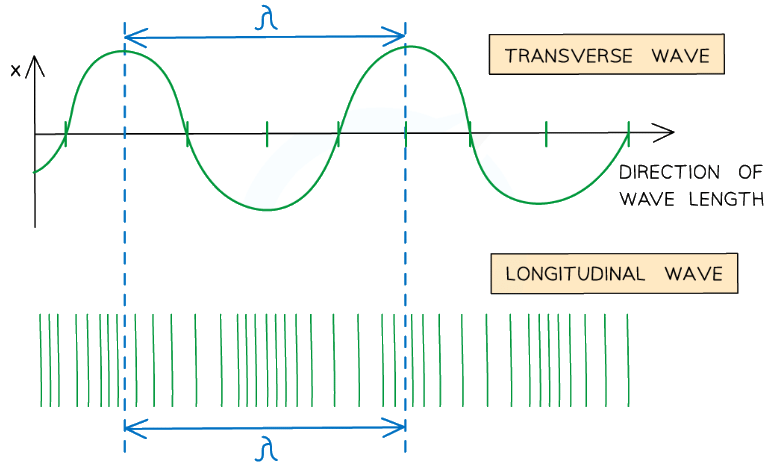 A wavelength on a longitudinal wave is the distance between two compressions or two rarefactions
A wavelength on a longitudinal wave is the distance between two compressions or two rarefactions
- Period (T) or time period, is the time taken for one complete oscillation or cycle of the wave Measured in seconds (s)
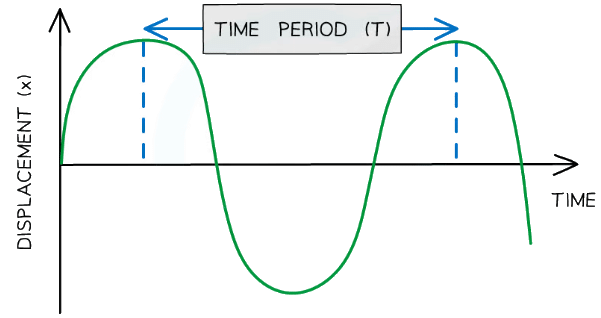 Diagram showing the time period of a wave
Diagram showing the time period of a wave
- Frequency (f) is the number of complete oscillations or wavelengths passing a point per unit time
Measured in Hertz (Hz) or s-1 - Speed (v) is the distance travelled by the wave per unit time, and defined by the wave equation
Measured in metres per second (m s-1)
Phase
- The phase difference tells us how much a point or a wave is in front or behind another
- It is defined as:
How far the cycle of one point is compared to another point on the same wave - This can be found from the relative positive of the crests or troughs of two different waves of the same frequency
- When the crests or troughs are aligned, the waves are in phase
- When the crest of one wave aligns with the trough of another, they are in antiphase
- The diagram below shows the green wave leads the purple wave by ¼ λ
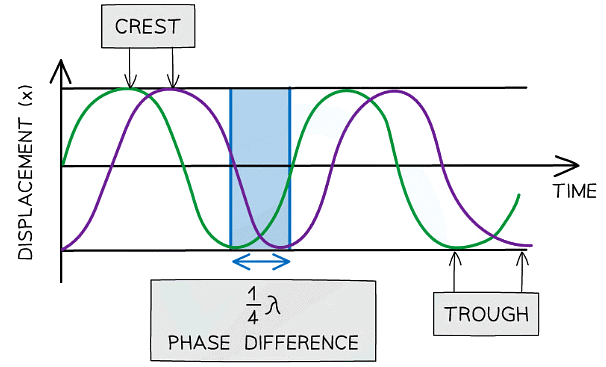
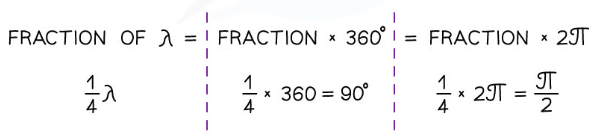 Two waves ¼ λ out of phase
Two waves ¼ λ out of phase
- In contrast, the purple wave is said to lag behind the green wave by ¼ λ
- Phase difference is measured in fractions of a wavelength, degrees or radians
- The phase difference can be calculated from two different points on the same wave or the same point on two different waves
- The phase difference between two points:
- In phase is 360o or 2π radians
- In anti-phase is 180o or π radians
Example: Plane waves on the surface of water at a particular instant are represented by the diagram below.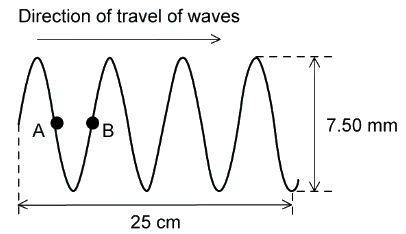
The waves have a frequency of 2.5 Hz. Determine:
(a) The amplitude
(b) The wavelength
(c) The phase difference between points A and B
A. The Amplitude
Maximum Displacement from The Equilibrium Position
7.50 mm ÷ 2 = 3.75 mm
B. The Wavelength
Distance Between Points on Successive Oscillations of The Wave That Are in Phase
From Diagram: 25cm = 33/4 Wavelengths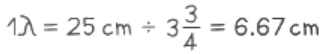
C. The Phase Difference Between Points A and B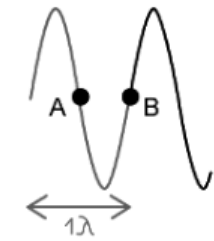
Points A and B Have 1/2 λ Difference = 1/2 × 360o = 180o
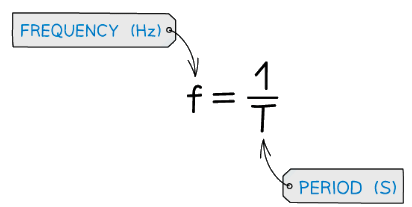
Calculating Frequency
Frequency (f) is defined by the equation: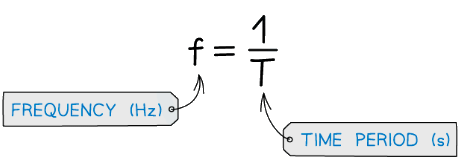
Where T is the time period, the time taken for one complete oscillation or cycle of the wave
Example: Calculate the frequency of the following wave: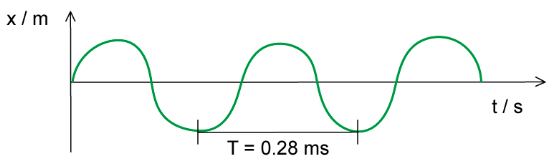
Step 1: List the known quantities
Period, T = 0.28 ms = 0.28 × 10-3 sStep 2: Write down the frequency equation
Step 3: Substitute in the values
f = 1 ÷ (0.28 × 10-3) = 3571.4 = 3.57 kHz
Determining Frequency from an Oscilloscope
- A Cathode-Ray Oscilloscope (CRO) is a laboratory instrument used to display, measure and analyse waveforms of electrical circuits
- The x-axis is the time-base and the y-axis is the voltage (or y-gain)
- The time-base is important for calculating the frequency of the signal
 Diagram of Cathode-Ray Oscilloscope display showing wavelength and time-base setting
Diagram of Cathode-Ray Oscilloscope display showing wavelength and time-base setting
- The frequency of a wave is determined from the time period of the wave
- The period can be determined from the time-base
- This is how many seconds each division represents measured commonly in s div-1 or s cm-1
- Dividing the total time by the number of wavelengths will give a value for T
- Use as many wavelengths shown on the screen as possible to reduce uncertainties
- The frequency is then determined using the equation:
Example: A cathode-ray oscilloscope (c.r.o.) is used to display the trace from a sound wave. The time-base is set at 7 µs mm-1.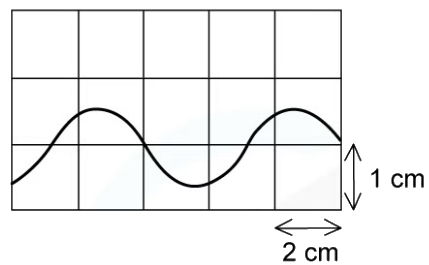
What is the frequency of the sound wave?
(a) 2.4 Hz
(b) 24 Hz
(c) 2.4 kHz
(d) 24 kHz
Ans. c
The Wave Equation
- The wave equation links the speed, frequency and wavelength of a wave
- This is relevant for both transverse and longitudinal waves
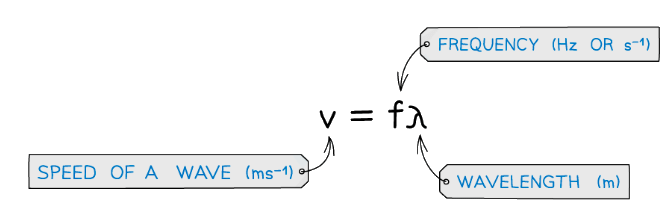
The wave equation shows that for a wave of constant speed:
- As the wavelength increases, the frequency decreases
- As the wavelength decreases, the frequency increases
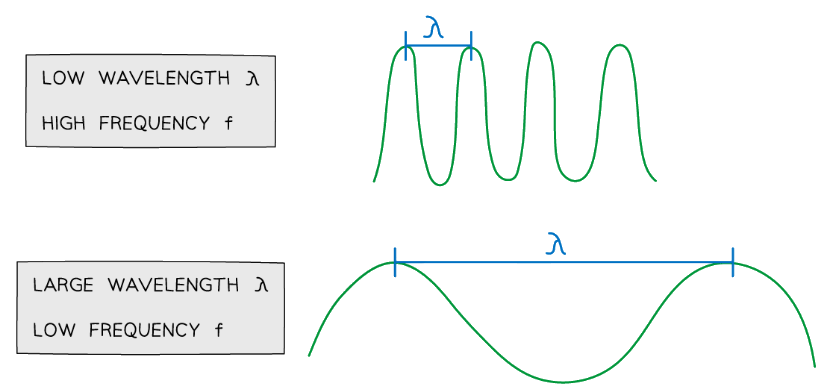 The relationship between frequency and wavelength of a wave
The relationship between frequency and wavelength of a wave
Example: The wave in the diagram below has a speed of 340 m s–1.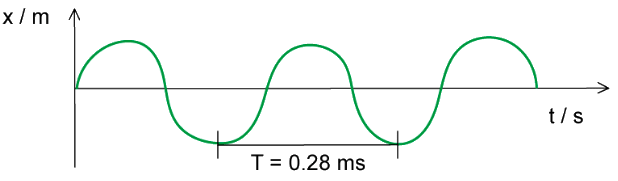
What is the wavelength of the wave?
Graphical Representations of Transverse & Longitudinal Waves
Transverse and longitudinal waves can be represented graphically
Transverse Waves
- Transverse waves show areas of crests (peaks) and troughs
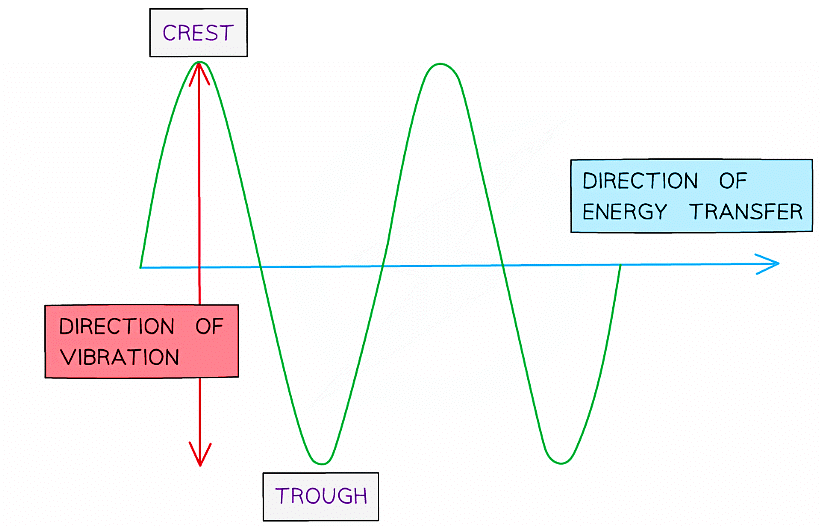 Diagram of a transverse wave
Diagram of a transverse wave
- The peaks are the maximum positive displacements
- The troughs are the maximum negative displacements
- The direction of the energy transfer is perpendicular to the direction of vibration of the particles in the wave
Longitudinal Waves
- Longitudinal waves show areas of compressions and rarefactions
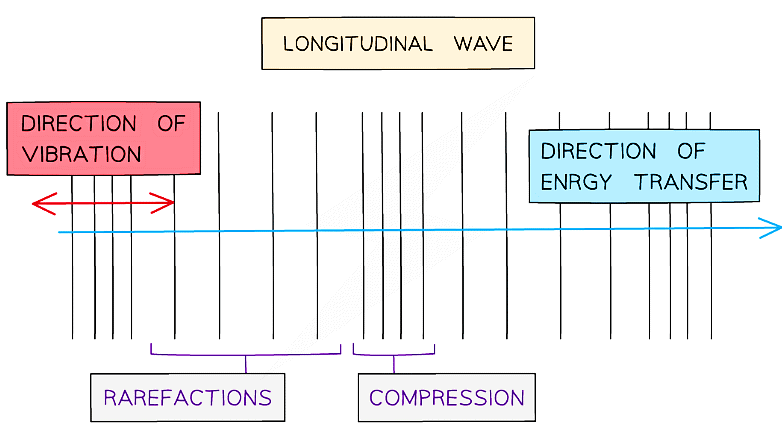 Diagram of a longitudinal wave
Diagram of a longitudinal wave
- The compressions are areas of high pressure due to particles being close together.
- The rarefactions are areas of low pressure due to the particles spread further apart
- The direction of energy transfer is parallel to the direction of vibration of the particles in the wave
Example: The graph shows how the displacement of a particle in a wave varies with time.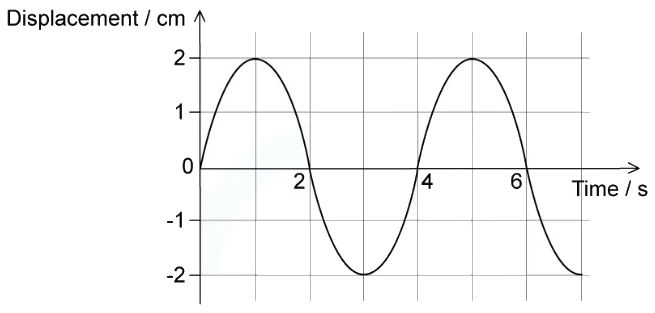 Which statement is correct?
Which statement is correct?
(a) The wave has an amplitude of 2 cm and could be either transverse or longitudinal.
(b) The wave has an amplitude of 2 cm and has a time period of 6 s.
(c) The wave has an amplitude of 4 cm and has a time period of 4 s.
(d) The wave has an amplitude of 4 cm and must be transverse.
Ans. a
The Waves Amplitude is the Displacement from The Equilibrium Position
From The Graph, this is 2 Cm
The Graph is Displacement Against Time, Not Displacement Against Direction of Wave Travel
Therefore, The Wave Could Be Either Transverse or Longitudinal
Demonstrating Waves Using a Ripple Tank
Waves can also be demonstrated by ripple tanks
- These produce a combination of transverse and longitudinal waves
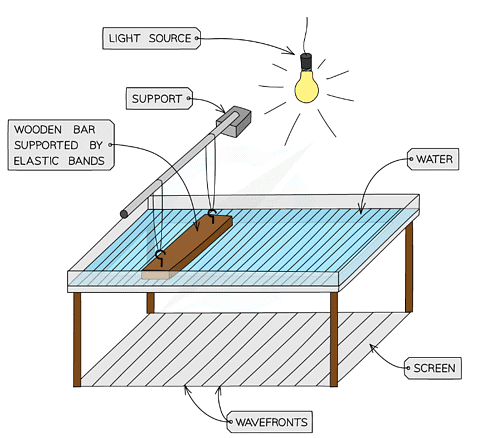 Wave effects can be demonstrated using a ripple tank
Wave effects can be demonstrated using a ripple tank
- In a ripple tank, a motorised wooden straight-edged bar produces plane (straight) waves while a small dipper produces circular waves
- When a light is shone from above, the bright bands seen on the screen below the tank show the wave crests (wavefronts)
- This makes it possible to measure the wavelength of the water waves and investigate the angles of reflection and refraction
- Reflection can be investigated using plane and curved surfaces, and the angles of incidence and reflection measured with respect to the normal
- Refraction can be investigated using a glass sheet to decrease the water depth and produce a region with a different wave speed
- If the separation of the wavefronts decreases, this shows they are travelling more slowly and vice versa
- Changing the angle of the wooden bar causes the wavefronts to go in a different direction
- The ripple tank, therefore, can also be used to study interference and diffraction
Intensity of a Progressive Wave
Progressive waves transfer energy
- The amount of energy passing through a unit area per unit time is the intensity of the wave
- Therefore, the intensity is defined as power per unit area
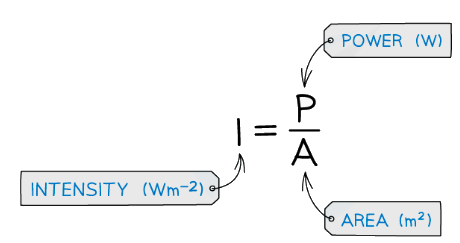
- The unit of intensity is Watts per metre squared (W m-2)
- The area the wave passes through is perpendicular to the direction of its velocity
- The intensity of a progressive wave is also proportional to its amplitude squared and frequency squared
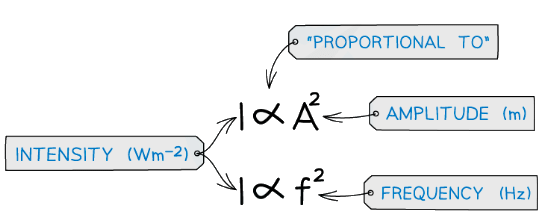
- This means that if the frequency or the amplitude is doubled, the intensity increases by a factor of 4 (22)
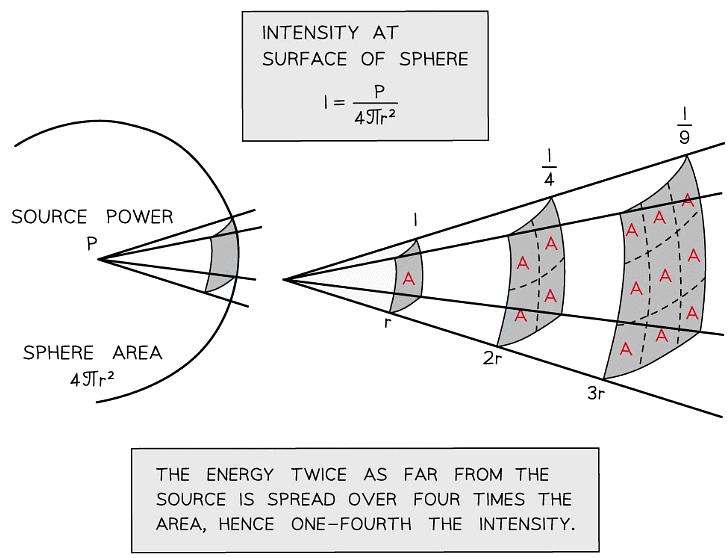
Spherical waves
- A spherical wave is a wave from a point source which spreads out equally in all directions
- The area the wave passes through is the surface area of a sphere: 4πr2
- As the wave travels further from the source, the energy it carries passes through increasingly larger areas as shown in the diagram below:
 Intensity is proportional to the amplitude squared
Intensity is proportional to the amplitude squared
- Assuming there’s no absorption of the wave energy, the intensity I decreases with increasing distance from the source
- Note the intensity is proportional to 1 / r2
- This means when the source is twice as far away, the intensity is 4 times less
- The 1 / r2 relationship is known in physics as the inverse square law
Example: The intensity of a progressive wave is proportional to the square of the amplitude of the wave. It is also proportional to the square of the frequency. The variation with time t of displacement x of particles when two progressive waves Q and P pass separately through a medium are shown on the graphs.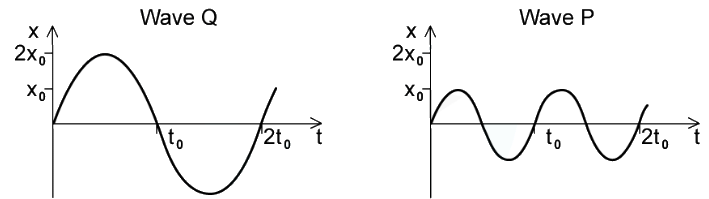
The intensity of wave Q is I0.What is the intensity of wave P?
|
142 videos|312 docs|132 tests
|