M-way Search Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
m-WAY Search Trees | Set-1 ( Searching )
The m-way search trees are multi-way trees which are generalised versions of binary trees where each node contains multiple elements. In an m-Way tree of order m, each node contains a maximum of m – 1 elements and m children.
The goal of m-Way search tree of height h calls for O(h) no. of accesses for an insert/delete/retrieval operation. Hence, it ensures that the height h is close to log_m(n + 1).
The number of elements in an m-Way search tree of height h ranges from a minimum of h to a maximum of mh -1.
An m-Way search tree of n elements ranges from a minimum height of log_m(n+1) to a maximum of n
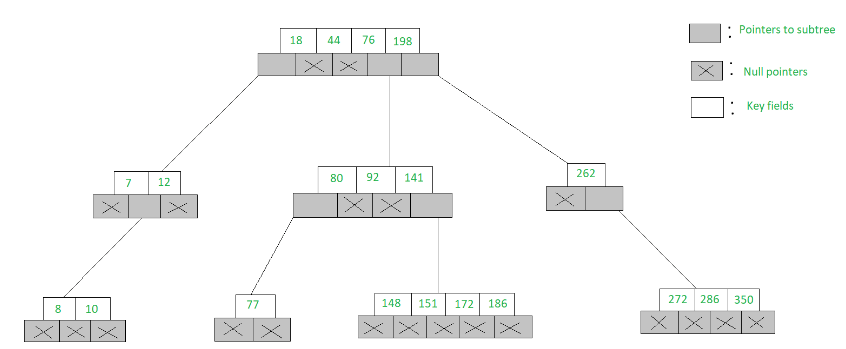
An example of a 5-Way search tree is shown in the figure below. Observe how each node has at most 5 child nodes & therefore has at most 4 keys contained in it.
The structure of a node of an m-Way tree is given below:
struct node {
int count;
int value[MAX + 1];
struct node* child[MAX + 1];
};
- Here, count represents the number of children that a particular node has
- The values of a node stored in the array value
- The addresses of child nodes are stored in the child array
- The MAX macro signifies the maximum number of values that a particular node can contain
Searching in an m-Way search tree:
- Searching for a key in an m-Way search tree is similar to that of binary search tree
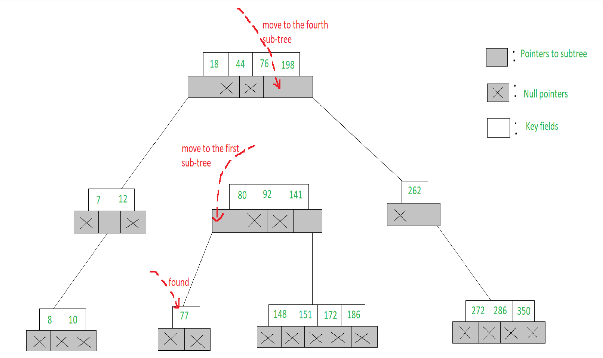
- To search for 77 in the 5-Way search tree, shown in the figure, we begin at the root & as 77> 76> 44> 18, move to the fourth sub-tree
- In the root node of the fourth sub-tree, 77< 80 & therefore we move to the first sub-tree of the node. Since 77 is available in the only node of this sub-tree, we claim 77 was successfully searched
// Searches value in the node
struct node* search(int val,
struct node* root,
int* pos)
{
// if root is Null then return
if (root == NULL)
return NULL;
else {
// if node is found
if (searchnode(val, root, pos))
return root;
// if not then search in child nodes
else
return search(val,
root->child[*pos],
pos);
}
}
// Searches the node
int searchnode(int val,
struct node* n,
int* pos)
{
// if val is less than node->value[1]
if (val < n->value[1]) {
*pos = 0;
return 0;
}
// if the val is greater
else {
*pos = n->count;
// check in the child array
// for correct position
while ((val < n->value[*pos])
&& *pos > 1)
(*pos)--;
if (val == n->value[*pos])
return 1;
else
return 0;
}
}
search():
- The function search() receives three parameters
- The first parameter is the value to be searched, second is the address of the node from where the search is to be performed and third is the address of a variable that is used to store the position of the value once found
- Initially a condition is checked whether the address of the node being searched is NULL
- If it is, then simply a NULL value is returned
- Otherwise, a function searchnode() is called which actually searches the given value
- If the search is successful the address of the node in which the value is found is returned
- If the search is unsuccessful then a recursive call is made to the search() function for the child of the current node
searchnode():
- The function searchnode() receives three parameters
- The first parameter is the value that is to be searched
- The second parameter is the address of the node in which the search is to be performed and third is a pointer pos that holds the address of a variable in which the position of the value that once found is stored
- This function returns a value 0 if the search is unsuccessful and 1 if it is successful
- In this function initially it is checked whether the value that is to be searched is less than the very first value of the node
- If it is then it indicates that the value is not present in the current node. Hence, a value 0 is assigned in the variable that is pointed to by pos and 0 is returned, as the search is unsuccessful
m-Way Search Tree | Set-2 | Insertion and Deletion
Insertion in an m-Way search tree:
The insertion in an m-Way search tree is similar to binary trees but there should be no more than m-1 elements in a node. If the node is full then a child node will be created to insert the further elements.
Let us see the example given below to insert an element in an m-Way search tree.
Example:
- To insert a new element into an m-Way search tree we proceed in the same way as one would in order to search for the element
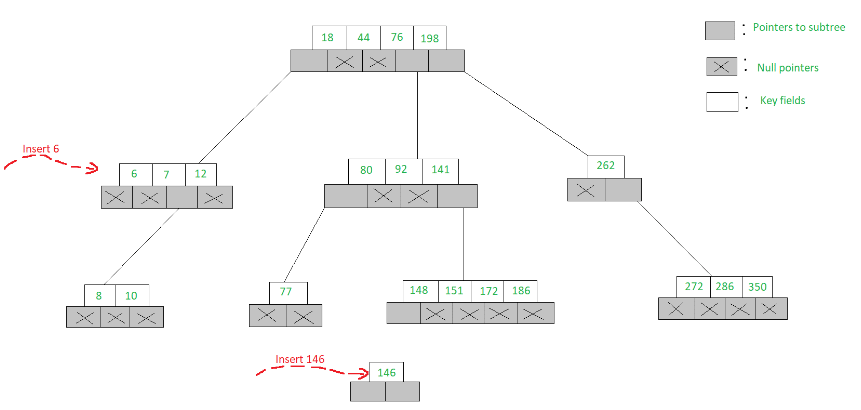
- To insert 6 into the 5-Way search tree shown in the figure, we proceed to search for 6 and find that we fall off the tree at the node [7, 12] with the first child node showing a null pointer
- Since the node has only two keys and a 5-Way search tree can accommodate up to 4 keys in a node, 6 is inserted into the node like [6, 7, 12]
- But to insert 146, the node [148, 151, 172, 186] is already full, hence we open a new child node and insert 146 into it. Both these insertions have been illustrated below
// Inserts a value in the m-Way tree
struct node* insert(int val,
struct node* root)
{
int i;
struct node *c, *n;
int flag;
// Function setval() is called which
// returns a value 0 if the new value
// is inserted in the tree, otherwise
// it returns a value 1
flag = setval(val, root, &i, &c);
if (flag) {
n = (struct node*)malloc(sizeof(struct node));
n->count = 1;
n->value[1] = i;
n->child[0] = root;
n->child[1] = c;
return n;
}
return root;
}
insert():
- The function insert() receives two parameters-the address of the new node and the value that is inserted
- This function calls a function setval() which returns a value 0 if the new value is inserted in the tree, otherwise it returns a value 1
- If it returns 1 then memory is allocated for new node, the variable count is assigned a value 1 and the new value is inserted in the node
- Then the addresses of the child nodes are stored in child pointers and finally the address of the node is returned
// Sets the value in the node
int setval(int val,
struct node* n,
int* p,
struct node** c)
{
int k;
// if node is null
if (n == NULL) {
*p = val;
*c = NULL;
return 1;
}
else {
// Checks whether the value to be
// inserted is present or not
if (searchnode(val, n, &k))
printf("Key value already exists\n");
// The if-else condition checks whether
// the number of nodes is greater or less
// than the maximum number. If it is less
// then it inserts the new value in the
// same level node, otherwise, it splits the
// node and then inserts the value
if (setval(val, n->child[k], p, c)) {
// if the count is less than the max
if (n->count < MAX) {
fillnode(*p, *c, n, k);
return 0;
}
else {
// Insert by splitting
split(*p, *c, n, k, p, c);
return 1;
}
}
return 0;
}
}
setval():
- The function setval() receives four parameters
- The first argument is the value that is to be inserted
- The second argument is the address of the node
- The third argument is an integer pointer that points to a local flag variable defined in the function insert()
- The last argument is a pointer to pointer to the child node that will be set in a function called from this function
- The function setval() returns a flag value that indicates whether the value is inserted or not
- If the node is empty then this function calls a function searchnode() that checks whether the value already exists in the tree
- If the value already exists then a suitable message is displayed
- Then a recursive call is made to the function setval() for the child of the node
- If this time the function returns a value 1 it means the value is not inserted
- Then a condition is checked whether the node is full or not
- If the node is not full then a function fillnode() is called that fills the value in the node hence at this point a value 0 is returned
- If the node is full then a function split() called that splits the existing node. At this point, a value 1 is returned to add the current value to the new node
// Adjusts the value of the node
void fillnode(int val,
struct node* c,
struct node* n,
int k)
{
int i;
// Shifting the node by one position
for (i = n->count; i > k; i--) {
n->value[i + 1] = n->value[i];
n->child[i + 1] = n->child[i];
}
n->value[k + 1] = val;
n->child[k + 1] = c;
n->count++;
}
fillnode():
- The function fillnode() receives four parameters
- The first is the value that is to be inserted
- The second is the address of the child node of the new value that is to be inserted
- The third is the address of the node in which the new value is to be inserted
- The last parameter is the position of the node where the new value is to be inserted
// Splits the node
void split(int val,
struct node* c,
struct node* n,
int k, int* y,
struct node** newnode)
{
int i, mid;
if (k <= MIN)
mid = MIN;
else
mid = MIN + 1;
// Allocating the memory for a new node
*newnode = (struct node*)
malloc(sizeof(struct node));
for (i = mid + 1; i <= MAX; i++) {
(*newnode)->value[i - mid] = n->value[i];
(*newnode)->child[i - mid] = n->child[i];
}
(*newnode)->count = MAX - mid;
n->count = mid;
// it checks whether the new value
// that is to be inserted is inserted
// at a position less than or equal
// to minimum values required in a node
if (k <= MIN)
fillnode(val, c, n, k);
else
fillnode(val, c, *newnode, k - mid);
*y = n->value[n->count];
(*newnode)->child[0] = n->child[n->count];
n->count--;
}
split():
- The function split() receives six parameters
- The first four parameters are exactly the same as in the case of function fillnode()
- The fifth parameter is a pointer to variable that holds the value from where the node is split
- The last parameter is a pointer to pointer of the new node created at the time of split
- In this function firstly it is checked whether the new value that is to be inserted is inserted at a position less than or equal to minimum values required in a node
- If the condition is satisfied then the node is split at the position MIN
- Otherwise, the node is split at one position more than MIN
- Then dynamically memory is allocated for a new node
- Next, a for loop is executed which copies into the new node the values and children that occur on the right side of the value from where the node is split
Deletion in an m-Way search tree:
Let K be a key to be deleted from the m-Way search tree. To delete the key we proceed as one would to search for the key. Let the node accommodating the key be as illustrated below.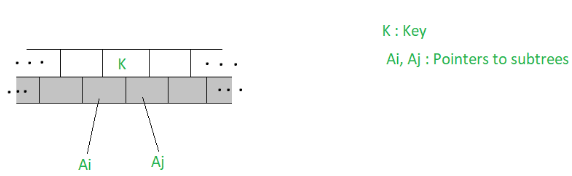
Approach:
There are several cases for deletion
- If (Ai = Aj = NULL) then delete K
- If (Ai != NULL, Aj = NULL) then choose the largest of the key elements K’ in the child node pointed to by Ai, delete the key K’ and replace K by K’
- Obviously deletion of K’ may call for subsequent replacements and therefore deletions in a similar manner, to enable the key K’ move up the tree
- If (Ai = NULL, Aj != NULL) then choose the smallest of the key element K” from the sub-tree pointed to by Aj, delete K” and replace K by K”
- Again deletion of K” may trigger subsequent replacements and deletions to enable K” move up the tree
- If (Ai !=NULL, Aj != NULL) then choose either the largest of the key elements K’ in the sub-tree pointed to by Ai, or the smallest of the key elements K” from the sub-tree pointed to by Aj to replace K
- As mentioned before, to move K’ or K” up the tree it may call for subsequent replacements and deletions
Example:
- To delete 151, we search for 151 and observe that in the leaf node [148, 151, 172, 186] where it is present, both its left sub-tree pointer and right sub-tree pointer are such that (Ai = Aj = NULL)
- We therefore simply delete 151 and the node becomes [148, 172, 186]. Deletion of 92 also follows a similar process
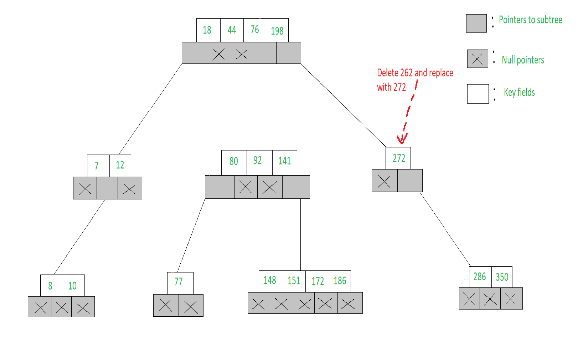
- To delete 262, we find its left and right sub-tree pointers Ai</sub and Aj respectively, are such that (Ai = Aj = NULL)
- Hence we choose the smallest element 272 from the child node [272, 286, 350], delete 272 and replace 262 with 272. Note that, to delete 272 the deletion procedure needs to be observed again
This deletion is illustrated below
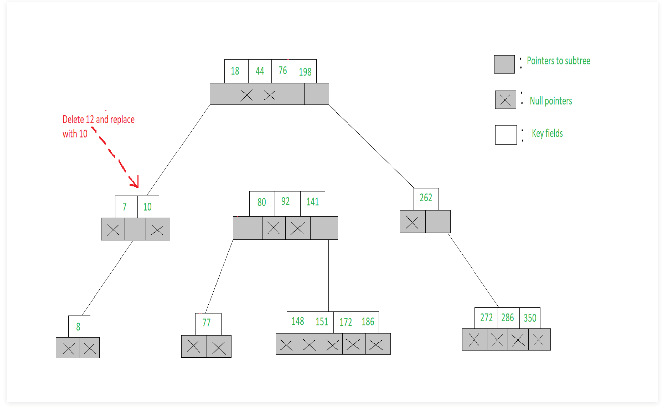
- To delete 12, we find the node [7, 12] accommodates 12 and the key satisfies (Ai != NULL, Aj = NULL)
- Hence we choose the largest of the keys from the node pointed to by Ai, viz., 10 and replace 12 with 10. This deletion is illustrated below
// Deletes value from the node
struct node* del(int val,
struct node* root)
{
struct node* temp;
if (!delhelp(val, root)) {
printf("\n");
printf("value %d not found.\n", val);
}
else {
if (root->count == 0) {
temp = root;
root = root->child[0];
free(temp);
}
}
return root;
}
del():
- The function del() receives two parameters. First is the value that is to be deleted second is the address of the root node
- This function calls another helper function delhelp() which returns value 0 if the deletion of the value is unsuccessful, 1 otherwise
- Otherwise, a condition is checked whether the count is 0
- If it is, then it indicates that the node from which the value is deleted is the last value
- Hence, the first child of the node is itself made the node and the original node is deleted. Finally, the address of the new root node is returned
// Helper function for del()
int delhelp(int val,
struct node* root)
{
int i;
int flag;
if (root == NULL)
return 0;
else {
// Again searches for the node
flag = searchnode(val,
root,
&i);
// if flag is true
if (flag) {
if (root->child[i - 1]) {
copysucc(root, i);
// delhelp() is called recursively
flag = delhelp(root->value[i],
root->child[i])
if (!flag)
{
printf("\n");
printf("value %d not found.\n", val);
}
}
else
clear(root, i);
}
else {
// Recursion
flag = delhelp(val, root->child[i]);
}
if (root->child[i] != NULL) {
if (root->child[i]->count < MIN)
restore(root, i);
}
return flag;
}
}
delhelp():
- The function delhelp() receives two parameters. First is the value to be deleted and the second is the address of the node from which it is to be deleted
- Initially it is checked whether the node is NULL
- If it is, then a value 0 is returned
- Otherwise, a call to function searchnode() is made
- If the value is found then another condition is checked to see whether there is any child to the value that is to be deleted
- If so, the function copysucc() is called which copies the successor of the value to be deleted and then a recursive call is made to the function delhelp() for the value that is to be deleted and its child
- If the child is empty then a call to function clear() is made which deletes the value
- If the searchnode() function fails then a recursive call is made to function delhelp() by passing the address of the child
- If the child of the node is not empty, then a function restore() is called to merge the child with its siblings
- Finally the value of the flag is returned which is set as a returned value of the function searchnode()
// Removes the value from the
// node and adjusts the values
void clear(struct node* m, int k)
{
int i;
for (i = k + 1; i <= m->count; i++) {
m->value[i - 1] = m->value[i];
m->child[i - 1] = m->child[i];
}
m->count--;
}
clear():
- The function clear() receives two parameters. First is the address of the node from which the value is to be deleted and second is the position of the value that is to be deleted
- This function simply shifts the values one place to the left from the position where the value is to be deleted is present
// Copies the successor of the
// value that is to be deleted
void copysucc(struct node* m, int i)
{
struct node* temp;
temp = p->child[i];
while (temp->child[0])
temp = temp->child[0];
p->value[i] = temp->value[i];
}
copysucc()
- The function copysucc() receives two parameters. First is the address of the node where the successor is to be copied and second is the position of the value that is to be overwritten with its successor
// Adjusts the node
void restore(struct node* m, int i)
{
if (i == 0) {
if (m->child[1]->count > MIN)
leftshift(m, 1);
else
merge(m, 1);
}
else {
if (i == m->count) {
if (m->child[i - 1]->count > MIN)
rightshift(m, i);
else
merge(m, i);
}
else {
if (m->child[i - 1]->count > MIN)
rightshift(m, i);
else {
if (m->child[i + 1]->count > MIN)
leftshift(m, i + 1);
else
merge(m, i);
}
}
}
}
restore():
- The function restore() receives two parameters. First is the node that is to be restored and second is the position of the value from where the values are restored
- If the second parameter is 0, then another condition is checked to find out whether the values present at the first child are more than the required minimum number of values
- If so, then a function leftshift() is called by passing the address of the node and a value 1 signifying that the value of this node is to be shifted from the first value
- If the condition is not satisfied then a funcition merge() is called for merging the two children of the node
// Adjusts the values and children
// while shifting the value from
// parent to right child
void rightshift(struct node* m, int k)
{
int i;
struct node* temp;
temp = m->child[k];
// Copying the nodes
for (i = temp->count; i > 0; i--) {
temp->value[i + 1] = temp->value[i];
temp->child[i + 1] = temp->child[i];
}
temp->child[1] = temp->child[0];
temp->count++;
temp->value[1] = m->value[k];
temp = m->child[k - 1];
m->value[k] = temp->value[temp->count];
m->child[k]->child[0]
= temp->child[temp->count];
temp->count--;
}
// Adjusts the values and children
// while shifting the value from
// parent to left child
void leftshift(struct node* m, int k)
{
int i;
struct node* temp;
temp = m->child[k - 1];
temp->count++;
temp->value[temp->count] = m->value[k];
temp->child[temp->count]
= m->child[k]->child[0];
temp = m->child[k];
m->value[k] = temp->value[1];
temp->child[0] = temp->child[1];
temp->count--;
for (i = 1; i <= temp->count; i++) {
temp->value[i] = temp->value[i + 1];
temp->child[i] = temp->child[i + 1];
}
}
rightshift() and leftshift()
- The function rightshift() receives two parameters
- First is the address of the node from where the value is shifted to its child and second is the position k of the value that is to be shifted
- The function leftshift() are exactly same as that of function rightshift()
- The function merge() receives two parameters. First is the address of the node from which the value is to copied to the child and second is the position of the value
// Merges two nodes
void merge(struct node* m, int k)
{
int i;
struct node *temp1, *temp2;
temp1 = m->child[k];
temp2 = m->child[k - 1];
temp2->count++;
temp2->value[temp2->count] = m->value[k];
temp2->child[temp2->count] = m->child[0];
for (i = 0; i <= temp1->count; i++) {
temp2->count++;
temp2->value[temp2->count] = temp1->value[i];
temp2->child[temp2->count] = temp1->child[i];
}
for (i = k; i < m->count; i++) {
m->value[i] = m->value[i + 1];
m->child[i] = m->child[i + 1];
}
m->count--;
free(temp1);
}
- The function merge() receives two parameters
- First is the address of the node from which the value is to be copied to the child and second is the position of the value
- In this function, two temporary variables temp1 and temp2 are defined to hold the addresses of the two children of the value that is to be copied
- Initially, the value of the node is copied to its child. Then the first child of the node is made the respective child of the node where the value is copied
- Then two for loops are executed, out of which first copies all the values and children of one child to the other child
- The second loop shifts the value and child of the node from where the value is copied
- Then the count of the node from where the node is copied is decremented. Finally, the memory occupied by the second node is released by calling free()
|
119 docs|30 tests
|
FAQs on M-way Search Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is an m-Way Search Tree? |  |
| 2. How does an m-Way Search Tree differ from a binary search tree? |  |
| 3. What are the advantages of using an m-Way Search Tree? |  |
| 4. How are elements searched in an m-Way Search Tree? |  |
| 5. How are elements inserted and deleted in an m-Way Search Tree? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|