Biot Savart Law and its Applications | Physics for JAMB PDF Download
Biot-Savart Law
Biot-Savart law gives the magnetic induction due to an infinitesimal current element.
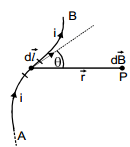
- Let AB be a conductor of an arbitrary shape carrying a current I, and P be a point in the vacuum at which the field is to be determined.
- Let us divide the conductor into infinitesimal current elements.
- Let
be a displacement vector from the element to the point P.
According to `Biot-Savart Law', the magnetic field induction at P due to the current element is given by
or
Where k is a proportionality constant.
Here vector points in the direction of current i.
In S.I. units,
The equation above is the vector form of the Biot-Savart Law. The magnitude of the field induction at P is given by:
,
where θ is the angle between and
.
If the medium is other than air or vacuum, the magnetic induction is:
where μr is the relative permeability of the medium and is a dimensionless quantity.
Applications of Biot-Savrat Law
Magnetic Field at an Axial Point of a Circular Point
Consider a circular loop of radius R and carrying a steady current i. We have to find out the magnetic field at the axial point P, which is at a distance x from the center of the loop.
Consider an element i of the loop as shown in the figure, and the distance of point P from the current element is r. The magnetic field at P due to this current element from the equation (1) can be given by,
In the case of a point on the axis of a circular coil, as for every current element, there is a symmetrically situated opposite element, the components of the field perpendicular to the axis cancel each other while along the axis add up.
Therefore, =
Here, q is the angle between the current element id and, which is everywhere and
sin  =
= =
Therefore, B =
or, B =
or, B =
If the coil has N turns, then
B =
Direction of 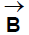 : The direction of the magnetic field at a point the axis of a circular coil is along the axis and its orientation can be obtained by using the right-hand thumb rule. If the figures are curled along the current, the stretched thumb will point toward the magnetic field.
: The direction of the magnetic field at a point the axis of a circular coil is along the axis and its orientation can be obtained by using the right-hand thumb rule. If the figures are curled along the current, the stretched thumb will point toward the magnetic field.
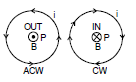
The magnetic field will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure given. Now consider some special cases involving the application of equation above.
Case I: Field at the center of the coil
In this case distance of the point P from the center (x) = 0, the magnetic field
B = =
Case II: Field at a point far away from the center
It means x >> R, B =
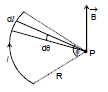
Magnetic Field at the Center of a Current Arc
Consider an arc of radius R carrying current I and subtending an angle f at the center.
According to Biot-Savart Law, the magnetic field induction at the point P is given by
B =
Here, dl = Rdθ
Therefore, B =
or, B =
It `l' is the length of the circular arc, we have
B =
Consider some special cases involving the application of the equation above.
Case I: If the loop is semicircular
In this case 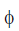 = π, so
= π, so
B = 
and will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure.
Case II: If the loop is a full circle with N turns
In this case  = 2p, so
= 2p, so
B =
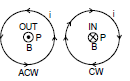
and will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure.
Example 1: Two-wire loop PQRSP formed by joining two semicircular wires of radii R1 and R2 carries a current i as shown in the figure given below. What is the magnetic field induction at the center O in cases (A) and (B)?
Solution: (a) As point O is along the length of the straight wires, the field at O due to them will be zero and hence the magnetic field is only due to semicircular portions
Therefore,
or, =
out of the page
(b) =
into the page
Example 2: A battery is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R as shown in the figure given below. One of the arcs AB of the ring subtends an angle q at the center. What is the value of the magnetic field at the center due to the current in the ring?
Sol. (a) As the field due to the arc at the center is given by
B =
Therefore, B =
But (VA - VB) = i1R1 = i2R2
or, i2 = i1 = i1
[Therefore, R µ L]
i2 = i1 [Therefore, L = rq]
Therefore, BR =
i.e., the field at the center of the coil is zero and is independent of θ.
Example 3: A charge of one coulomb is placed at one end of a nonconducting rod of length 0.6m. The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with an angular frequency 104π rad/s. Find the magnetic field at a point on the axis of rotation at a distance of 0.8 m from the center of the path.
Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about a horizontal axis passing through the mid-point of the rod with the same angular frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4 m from the center of the rod.
Solution: As the revolving charge q is equivalent to a current
i = qf = q × = 1 ×
= 5 × 103 A
Now B =
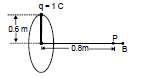
Therefore, B = 10-7 × = 1.13 × 10-3 T
If half of the charge is placed at the other end and the rod is rotated at the same frequency, the equivalent current.
i' = = qf = i = 5 × 103 A
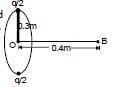
In this case, R' = 0.3 m and x' = 0.4 m
Therefore, B' = 10-7 × = 2.3 × 10-3T
Magnetic Field on a Current-Carrying Conductor
When Wire is of Finite Length
- Consider a straight wire segment carrying a current i and there is a point P at which the magnetic field is to be calculated as shown in the figure.
- This wire segment makes angles θ1 and θ2 at that point with normal OP.
- Consider an element of length dy at a distance y from O and the distance of this element from point P is r and the line joining P to Q makes an angle q with the direction of current as shown in the figure. Using Biot-Savart Law magnetic field at point P due to small current element is given by
- As every element of the wire contributes to
in the same direction, we have
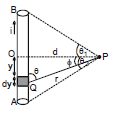
From the triangle OPQ, as shown in the diagram, we have
y = d tan 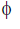
or dy = d sec2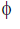 d
d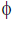
and is the same triangle,
r = d sec  and q = (90º -
and q = (90º -  ), where
), where  is the angle between line OP and PQ
is the angle between line OP and PQ
Now equation (i) can be written in this form
or
Note: θ1 & θ2 must be taken with the sign.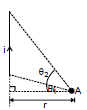
In the case shown in the figure,
B at A =
The direction of 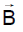 : The direction of the magnetic field is determined by the cross product of the vector
: The direction of the magnetic field is determined by the cross product of the vector with
. Therefore, at point P, the direction of the magnetic field due to the whole conductor will be perpendicular to the plane of the paper and going into the plane.
Right-hand Thumb Rule: The direction of B at point P due to a long, straight wire can be found by the right-hand thumb rule. The direction of the magnetic field is perpendicular to the plane containing the wire and perpendicular to the point. The orientation of the magnetic field is given by the direction of the curl fingers if we stretch the thumb along the wire in the direction of the current. Refer figure.
Conventionally, the direction of the field perpendicular to the plane of the paper is represented by if into the page and by
if out of the page.
Now consider some special cases involving the application of equation (3)
Case 1: When the point P is on the perpendicular bisector
In this case angle θ1 = θ2, using the result of equation (3), the magnetic field is
where 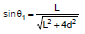
Case 2: If the wire is infinitely long
f the wire is infinitely long then the magnetic field at `P' (as shown in the figure) is given by (using q1 = q2 = 90° and the formula `B' due to straight wire)
B = ⇒ B µ
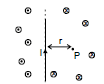
The direction of at various is as shown in the figure. The magnetic lines of force will be concentric circles around the wire (as shown earlier)
Case 3: When the point lies along the length of the wire (but not on it)
If the point P is along the length of the wire (but not one it), then as and
will either be parallel or antiparallel, i.e., q = 0 or p, so
and hence using equation (1)
Example 4: Calculate the magnetic field induction at a point distance, metre from a straight wire of length `a' metre carrying a current of I amp. The point is on the perpendicular bisector of the wire.
Solution: B = [sinq1 + sinq2]
= 10-7
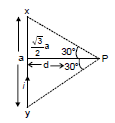
=
Perpendicular to the plane of figure (inward).
Example 5: Find the resultant magnetic field at `C' in the figure shown.
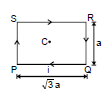
Solution: It is clear that `B' at `C' due to all the wires being directed Ä. Also, B at `C due to PQ and SR being the same. Also due to QR and PS being the same
Therefore, Bres = 2(BPQ + BSP)
BPQ = (sin 60° + sin 60°)
BSP = (sin 30° + sin 30°)
⇒ Bres = =
Example 6: The figure shows a square loop made from a uniform wire. Find the magnetic field at the center of the square if a battery is connected between points A and C.
Solution: The current will be equally divided at A. The fields at the center due to the currents in the wires AB and DC will be equal in magnitude and opposite in direction. The result of these two fields will be zero. Similarly, the resultant of the fields due to the wires AD and BC will be zero. Hence, the net field at the center will be zero.
Example 7: In the figure shown there are two parallel long wires (placed in the plane of the paper) carrying currents 2 I and I consider points A, C, D on the line perpendicular to both the wires and also in the plane of the paper. The distances are mentioned.
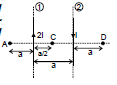
Find (i) at A, C, D
(ii) position of point on line A C D where is zero.
Solution: (i) Let us call due to (1) and (2) as
and
respectively. Then
at A: is
and
is
B1 = and B2 =
Therefore, Bres = B1 - B2 =
Ans.
at C: is
and
also
Therefore, Bres = B1 + B2 =
+
=
=
Ans.
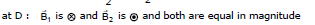
Therefore, Bres = 0 Ans.
(ii) It is clear from the above solution that B = 0 at point `D'.
|
260 videos|253 docs|230 tests
|
FAQs on Biot Savart Law and its Applications - Physics for JAMB
| 1. What is the Biot-Savart law? |  |
| 2. How can the Biot-Savart law be applied to calculate the magnetic field? |  |
| 3. Can the Biot-Savart law be used to calculate the magnetic field of a solenoid or a coil? |  |
| 4. How does the Biot-Savart law relate to Ampere's law? |  |
| 5. What are some practical applications of the Biot-Savart law? |  |

















