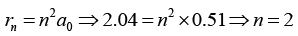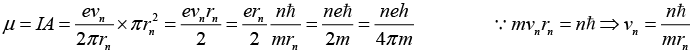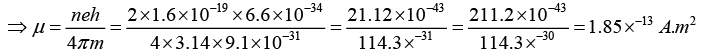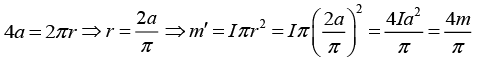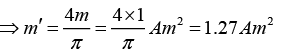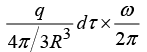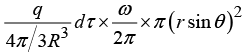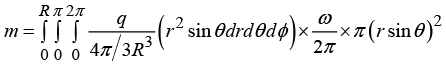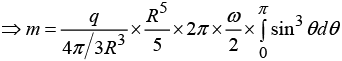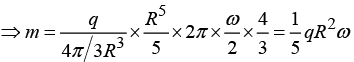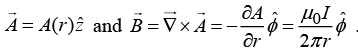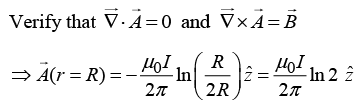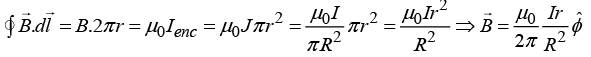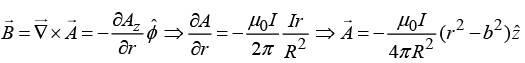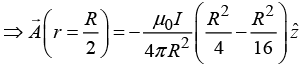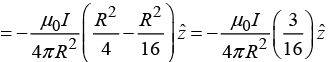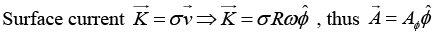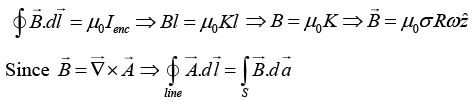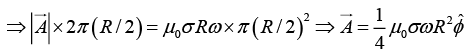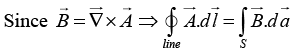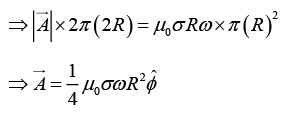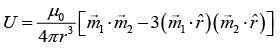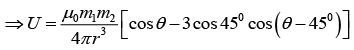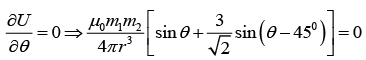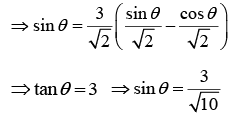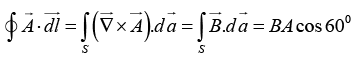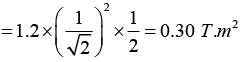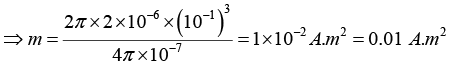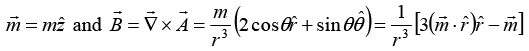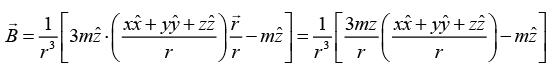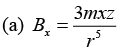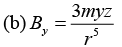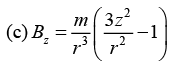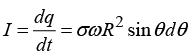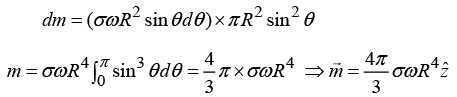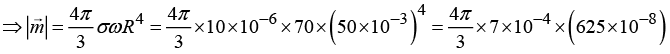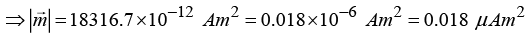Magnetic Vector Potential, Magnetic Dipole: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. Find the magnetic moment of an electron of charge e and mass m moving in a Bohr orbit of radius 2.040A in an Hydrogen atom
Q.2. The magnitude of the magnetic dipole moment associated with a square shaped loop carrying a steady current 0.5 A is 1.0 A.m2. If this loop is changed to a circular shape with the same current 0.5 A passing through it, then find the magnetic dipole moment.
Magnetic dipole moment associated with a square shaped loop (let side is a) carrying a steady current I is m = Ia2.
Magnetic dipole moment associated with a circular shaped loop (let radius is r) carrying a steady current I is m' = Iπr2.
Here
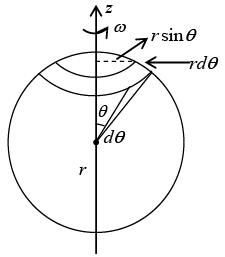
Q.3. A charge q is uniformly distributed over the volume of a uniform ball of radius R which rotates with angular velocity ω about the axis passing through its centre. Find the magnitude of the magnetic moment of the ball.
The magnetic moment must clearly be along the axis of rotation. Consider a volume
element dτ . It contains charge
The rotation of the sphere causes this charge to revolve around the axis and constitute a current:
Its magnetic moment will be
So total magnetic moment is
Q.4. (a) Find the magnetic vector potential at a distance R from an infinite straight wire carrying a current I. Take distance 2R as a reference point. Check that 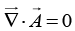 and
and 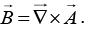
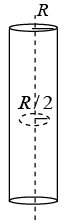
(b) Find the magnetic potential at a distance R /2, if it has radius R and the current is uniformly distributed. Take distance R /4 as a reference point.
(a)
point in the same direction as I and is a function of r (the distance from the wire).
In cylindrical coordinates
(b)
where b is arbitrary constant.
Q.5. An infinitely long hollow cylinder of radius a carrying R surface charge density σ is rotated about its cylindrical axis with a constant angular speed ω. Then find
(a) The magnitude of vector potential at a distance R /2 from its axis.
(b) The magnitude of vector potential at a distance 2R from its axis.
(a)
Magnetic field inside is
(b)
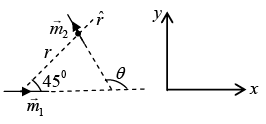
Q.6. A small magnetic needle is kept at (0, 0) with its moment along the x -axis. Another small magnetic needle is at the point (1,1) and is free to rotate in the xy - plane. Show that in the equilibrium sin θ = 3/√10. where angle q is the angle between their magnetic moments.
For stable position energy is minimum i.e.
Q.7. In a constant magnetic field of 1.2 Tesla along the z -direction, find the value of the path integral 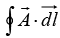 in the units of (Tesla m2) on a square loop of side length (1/√2) meters. The normal to the loop makes an angle of 60° to the z -axis, as shown in the figure.
in the units of (Tesla m2) on a square loop of side length (1/√2) meters. The normal to the loop makes an angle of 60° to the z -axis, as shown in the figure.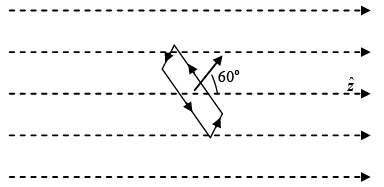
Q.8. Consider a thin round loop with current having radius of the loop equal to 100 mm and magnetic field at its centre is equal to 2μT. Then find the magnetic moment of the loop.
Magnetic moment
Q.9. The vector potential 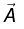 due to a magnetic moment
due to a magnetic moment 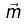 at a point
at a point 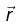 is given by
is given by 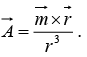 If
If 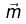 is directed along the positive z -axis, then find
is directed along the positive z -axis, then find
(a) x -component of 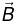
(b) y -component of 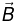
(c) z -component of 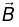
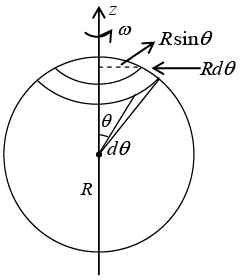
Q.10. A spherical shell of radius 50 mm carries a constant surface charge density 10 μC/m2 and is rotating about one of its diameters with an angular velocity 70 rad/sec. Find the magnitude of the magnetic moment of the shell.
The total charge on the shaded ring is dq = σ(2πR sin θ)Rd θ
Time for one revolution is dt = 2π/ω
⇒ Current in the ring
Area of the ring = π(R sin θ)2, so the magnetic moment of the ring is
|
82 videos|32 docs|22 tests
|