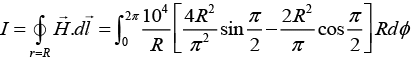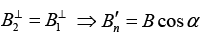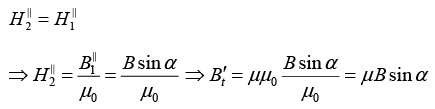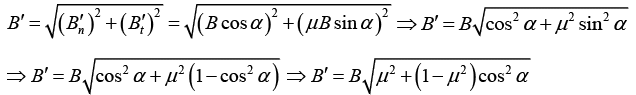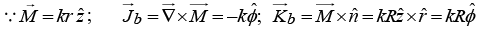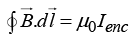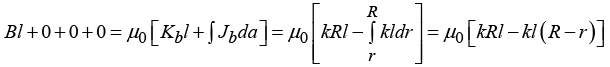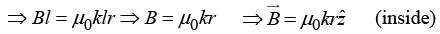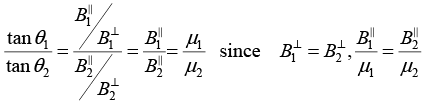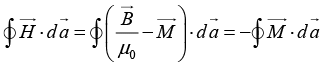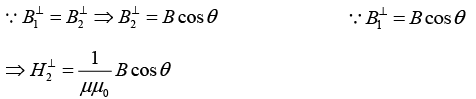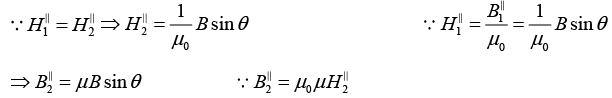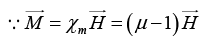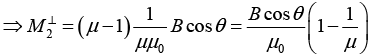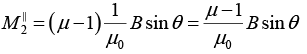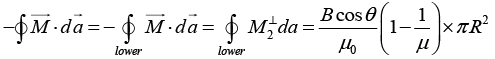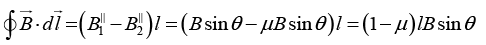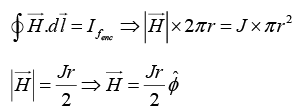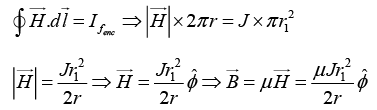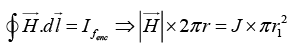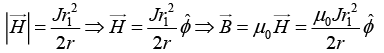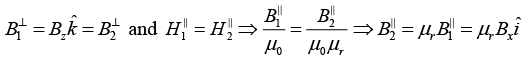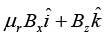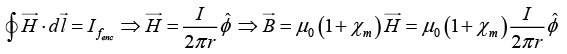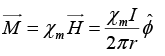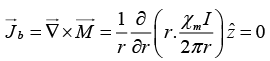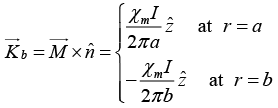Magnetisation & Boundary Condition: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. A circular conductor of radius R = 1 cm has an internal field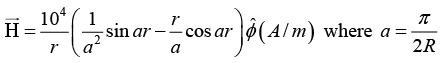
Then find the total current in the conductor.
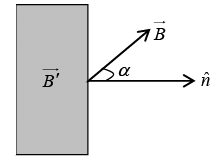
Q.2. The magnetic induction in vacuum at a plane surface of a uniform isotropic magnetic material is equal to B . The vector 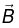 forms an angle α with the normal to the surface. The relative permeability of the magnetic material is equal to μ . Show that the magnitude of the magnetic induction B' in the magnetic material in the vicinity of its surface is
forms an angle α with the normal to the surface. The relative permeability of the magnetic material is equal to μ . Show that the magnitude of the magnetic induction B' in the magnetic material in the vicinity of its surface is
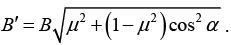
Thus
Q.3. A long circular cylinder of radius R carries a magnetization 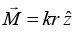 where k is a constant and r is the distance from the axis; there is no free current anywhere. Find
where k is a constant and r is the distance from the axis; there is no free current anywhere. Find
(a) all bound currents,
(b) the magnetic field due to  for points inside and outside the cylinder.
for points inside and outside the cylinder.
(a)
Thus current has solenoidal symmetry. This is essentially a superposition of solenoids. Magnetic field is in the z -direction.
(b) From Ampere’s Law:
Q.4. At the interface between two linear dielectrics (with permeability μ1 and μ2), the magnetic field lines bend, as shown in the figure. Assume that there is no free current at the interface. Find the ratio 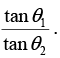

Q.5. The magnetic field in vacuum at a plane surface of a magnetic material is equal to 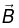 and the vector
and the vector 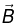 forms an angle θ with the normal
forms an angle θ with the normal  of the surface. The relative permeability of the magnetic material is equal to μ. Find:
of the surface. The relative permeability of the magnetic material is equal to μ. Find:
(a) The flux of the vector 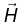 through the spherical surface S of radius R, whose centre lies on the surface of the magnetic material;
through the spherical surface S of radius R, whose centre lies on the surface of the magnetic material;
(b) The circulation of the vector 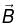 around the square path Γ with side ℓ located as shown in figure.
around the square path Γ with side ℓ located as shown in figure.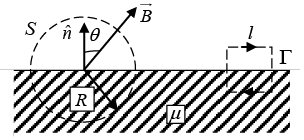
(a)
and
Thus
(b)
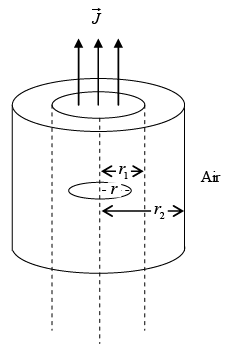
Q.6. An infinitely long solid cylindrical conductor of radius r1, carries a uniform volume current density 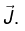 It is uniformly surrounded by another coaxial cylinder of a linear magnetic medium with permeability μ, up to radius r2 as shown in the figure.
It is uniformly surrounded by another coaxial cylinder of a linear magnetic medium with permeability μ, up to radius r2 as shown in the figure.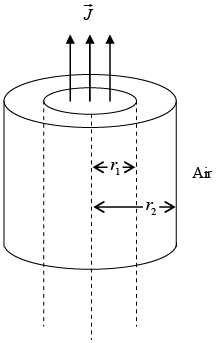
(a) Determine the magnetic field 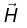 in the region r<r1 and magnetic induction
in the region r<r1 and magnetic induction
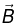 in the regions, r1< r<r2 and r>r2, where r is the radial distance from the axis of the cylinder.
in the regions, r1< r<r2 and r>r2, where r is the radial distance from the axis of the cylinder.
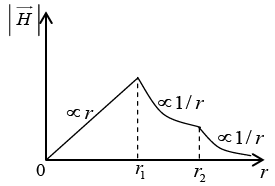
(b) Sketch the variation of 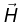 with r in all the three regions.
with r in all the three regions.
(a) Let us draw an amperian loop of radius r(r <r1)
Similarly draw an amperian loop of radius r(r1< r< r2)
Again draw an amperian loop of radius r(r >r2)
(b)
Q.7. The x - y plane is the boundary between free space and a magnetic material with relative permeability μr . The magnetic field in the free space is 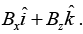 Then find the magnetic field in the magnetic material.
Then find the magnetic field in the magnetic material.
The magnetic field in the magnetic material is
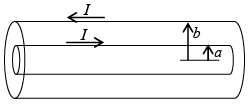
Q.8. A coaxial cable consists of two very long cylindrical tubes, separated by a material with susceptibility χm . A current I flows down the inner conductor and returns along the outer one; in each case the current distributes itself uniformly over the surface.
(a) Find the magnetic field in the region between the tubes.
(b) Find all bound currents.
(a)
(b)
and
|
82 videos|32 docs|22 tests
|