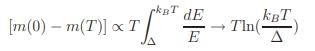Magnetism is one of the oldest phenomena in natural sciences. But to understand the physical process that give rise to the various magnetic properties of materials, we had to await the advent of modern quantum mechanics.
And this is due to intimate connection between magnetism and the electronic structure of matter. Considering the motion of a charged particle in a magnetic field, simple quantum mechanics having an essential magnetic-field dependent term in the Hamiltonian explains the origin of diamagnetism.
The competition between an aligning magnetic field and the randomizing thermal agitation gives rise to a net moment in paramagnets which can be quantified by the population-weighted contributions of electrons in different energy eigen-states. Spontaneous ordering in ferro- and antiferro-magnets for localized moments can be well-explained by the exchange coupling (due to Coulomb interaction along with the Pauli’s exclusion principle) whereas the magnetism of itinerant electrons originates from spin split of bands. These theories [1,2], valid for bulk magnetism, are not sufficient to explain the magnetic properties of low-dimensional systems, namely thin films or objects in nanometer scale as they are distinctly different due to changed density of states (DOS), reduced symmetry, finite size effect, lower co-ordination number etc.
Tremendous advancement in recent growth techniques such as molecular beam epitaxy, focused-ion and electron-beam lithography, self-assembled growth, physical and chemical vapor deposition, controlled chemical and electro-chemical processes allow us to fabricate high quality low dimensional systems providing wide opportunities for technology and new understanding in fundamental science. Parallel development of the characterization techniques made it possible to observe a series of exciting phenomenon like thickness dependent magnetization, re-orientation transition of ultrathin films, spin-vortices etc. in particular field of magnetism. Utilizing the intrinsic spin of electron, a plenty of techniques like spin polarized low energy electron diffraction (SPLEED), spin polarized electron energy loss spectroscopy (SPEELS) become popular to probe surface magnetism. Spin-resolved angleresolved ultra-violet photo-electron spectroscopy (SRARUPS) is another powerful technique for a detailed electronic structure to understand the role of ex-change interaction in itinerant electron systems. Similarly, spin polarized xray photoelectron spectroscopy (SPXPS) is useful technique regarding the local and element specific information about the magnetism. Polarized neutron reflectivity (PNR) is also very powerful to extract simultaneous information of the chemical structure as well as the magnetic structure. Moreover, PNR technique quantifies the magnetization in an absolute unit (Bohr magneton) as the magnetic intensity can be normalized by exactly the same number of scatterers those provide the structural intensity. Superconducting quantum interference device (SQUID), vibrating sample magnetometer (VSM), magnetic circular x-ray dichroism (XMCD) and magneto-optical Kerr effect (MOKE) are other popular techniques. Not only the magnetism of nano-structured systems, but also the magnetotransport (which deals with all kinds of change in electrical conductivity in presence of a magnetic field) keep on surprising us with fascinating phenomenon which includes giant magneto-resistance (GMR) [3, 4], tunnel magneto-resistance (TMR) [5, 6], domain-wall motion, spin-transfer-torque (STT) [7–11] effect etc. It was known that ferromagnetic metals (in general, a positive magneto-resistance (MR) is expected for bulk due to increase of effective path length in presence of a magnetic field, but the spin-split bands causes a negative MR) show different resistance depending upon the relative orientation between the direction of electrical current and magnetization — this phenomena is known as anisotropic magneto-resistance (AMR) (connected with the spin-orbit interaction and its influence on s-d scattering). However, the subject of magneto-transport was changed drastically since the discovery of GMR [4] in 1988 and opened up a wide opportunity to new efforts in study of magneto-transport properties of nano-structured materials. The idea of realization of memory bits by two different resistance states corresponding to a parallel (low-resistive state, LRS) or anti-parallel (highresistive state, HRS) alignment of magnetization of the two magnetic layers has revolutionize the concept of modern storage devices. Moreover, utilizing the spin rather than the charge of electron (as a result, the power consumption is minimum) has lead to a new field of ‘spintronics’ [12]. The phenomena of STT that induce current driven magnetization reversal in giant GMR and TMR devices, provides a possible way to realize current controlled switching of magnetic memory bits and nano-scale microwave oscillators without application of external magnetic field.
The scope of this thesis is to understand the magnetic ordering in low dimensional systems, in particular, gadolinium (Gd)-based ultra-thin film which is a good approximation of a two-dimensional (2d) magnetic system and to explore the role of anisotropy in defining the easy axis in an array of metal, namely, cobalt (Co) nanowires (NWs). In this thesis we also study the controlled electro-deposition and the magneto-transport of multi-stacked magnetic/non-magnetic NWs, namely cobalt/copper (Co/Cu) embedded in poly-carbonate template. Experimental details regarding the deposition processes and characterization techniques is included as a part of the discussion. This thesis is structured as follows:
- We start with a brief introduction to low dimensional magnetism in Chapter 1 and discuss the possibility of magnetic ordering in different theoretical models.
- The working principle of some instruments we have used, like scanning electron microscope (SEM), transmission electron microscope (TEM) etc. is briefly described in 2
- Chapter 3 includes the detail about deposition of ultra-thin film by Langmuir-Blodgett (LB) method. Grazing incidence x-ray reflectivity (GIXR) and polarized neutron reflectivity (PNR), useful techniques for characterization of thin films, is reviewed with necessary theoretical background. A versatile simulator, developed by us for reflectivity analysis is an essential part of this work.
- Template-based electro-deposition of NWs of magnetic metal (Co) and magnetic/non-magnetic (Co/Cu) bi-metal is discussed in Chapter 4 with their characterization using, mainly SEM and TEM.
- Chapter 5 discusses the results obtained in PNR study regarding the magnetic ordering in Gd-based LB film, explaining the apparent fielddependent saturation of magnetization caused due to presence of inplane spin-vortices.
- We discuss, in Chapter 6 the diameter dependence of magnetic properties, in particular, the enhancement of coercivity and squareness of the M-H loop on reduction of wire diameter in connection with the shape anisotropy and domain size. Moreover, the magneto-transport properties of array of Co/Cu NW embedded within template is also discussed. Huge resistive switching observed in sandwich-structured Co/Cu/Co NWs is discussed considering the STT effect. Moreover, the possibility of presence of oxide layer that also cause similar bi-stable switching due to formation and removal of conducting paths of sub-oxides through local redox processes is considered in a metal/insulator/metal(MIM) sandwich structure having no magnetic layer, namely Cu/CuxO/Au.
- Chapter 7 summarizes this thesis and closes with an outlook.
Magnetism in low dimensions: theoretical overview
When the dimensionality of a physical system is reduced, it is well known that the magnetic ordering tends to decrease as fluctuations become relatively important. Spin-lattice models predicts that an infinite one dimensional (1d) chain with short-range interactions spontaneously breaks up into segments with different orientation of magnetization, thereby prohibiting the long range ferromagnetic order at finite temperature. However, reduced coordination number in low dimension leads to enhancement in DOS near the Fermi level hence also the magnetic moment. As elucidated by the StonerWohlfarth criterion for itinerant ferromagnets (Jn0(EF ) > 1, J is the exchange constant), some metals which are not ferromagnetic in bulk may exhibit ferromagnetic behavior in low dimension. The substrate has a substantial role in such case of promotion to ferromagnet. The systems having nearest neighbour Heisenberg interaction 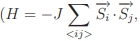 where J is the exchange integral and
where J is the exchange integral and 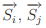 are the spins at i-th and j-th site, respectively), on the other hand, can show a variety of magnetic ordering depending upon the spin dimensionality, n and the space dimensionality, d. Exactly solvable 1d and 2d Ising (n=1) models have the transition temperature (below which an ordered state exists), Tc = 0 and a finite Tc, respectively, implying that 1d Ising system lacks long-range order (LRO) whereas spontaneous magnetization is expected for 2d Ising system at any finite temperature. The absence of LRO in 1d Ising model can be understood easily by considering the ex- citation of a 1d chain with free ends:
are the spins at i-th and j-th site, respectively), on the other hand, can show a variety of magnetic ordering depending upon the spin dimensionality, n and the space dimensionality, d. Exactly solvable 1d and 2d Ising (n=1) models have the transition temperature (below which an ordered state exists), Tc = 0 and a finite Tc, respectively, implying that 1d Ising system lacks long-range order (LRO) whereas spontaneous magnetization is expected for 2d Ising system at any finite temperature. The absence of LRO in 1d Ising model can be understood easily by considering the ex- citation of a 1d chain with free ends: 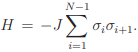 The excitation is nothing but the formation of a boundary (say, in-between i and i + 1-th site i.e. σi = 1 for i ≤ l, σi = −1 for i > l) between two different spinprojections which can occur in N − 1 ways. At any T ≠ 0, the change in free energy due to these excitations is 2J − kBTln(N − 1) which is less than zero for all T > 0 in the limit N → ∞. These excitations make the system disorder implying the expectation value of the magnetization to be zero. Therefore, there cannot be a phase transition to a ferromagnetic state in 1d Ising system with nearest-neighbor (or with any finite-range) interactions. If the Ising spins are placed on a 2d lattice, a phase transition to a magnetically ordered state below a non-zero critical temperature will result. This is because the energy cost and the entropy gain of making the boundary both scale with the perimeter size of the boundary. Energy and entropy therefore can have a fair fight with neither having an overwhelming advantage. Building on inequalities developed by Bogolubov and Hohenberg, the absence of LRO for isotropic, short-range interaction (more precisely, it must decrease more rapidly than 1/r3 ) in low-dimensions (d ≤ 2), is rigorously proved by Mermin and Wagner [13]. So for 2d XY (n=2) and 2d isotropic Heisenberg model (n=3) system no spontaneous magnetization is expected at any finite temperature. However, 2d XY (n=2) system is special to exhibit a continuous phase transition (known as the Berezinskii-Kosterlitz-Thouless (BKT) transition [14–18]) at a finite Tc.
The excitation is nothing but the formation of a boundary (say, in-between i and i + 1-th site i.e. σi = 1 for i ≤ l, σi = −1 for i > l) between two different spinprojections which can occur in N − 1 ways. At any T ≠ 0, the change in free energy due to these excitations is 2J − kBTln(N − 1) which is less than zero for all T > 0 in the limit N → ∞. These excitations make the system disorder implying the expectation value of the magnetization to be zero. Therefore, there cannot be a phase transition to a ferromagnetic state in 1d Ising system with nearest-neighbor (or with any finite-range) interactions. If the Ising spins are placed on a 2d lattice, a phase transition to a magnetically ordered state below a non-zero critical temperature will result. This is because the energy cost and the entropy gain of making the boundary both scale with the perimeter size of the boundary. Energy and entropy therefore can have a fair fight with neither having an overwhelming advantage. Building on inequalities developed by Bogolubov and Hohenberg, the absence of LRO for isotropic, short-range interaction (more precisely, it must decrease more rapidly than 1/r3 ) in low-dimensions (d ≤ 2), is rigorously proved by Mermin and Wagner [13]. So for 2d XY (n=2) and 2d isotropic Heisenberg model (n=3) system no spontaneous magnetization is expected at any finite temperature. However, 2d XY (n=2) system is special to exhibit a continuous phase transition (known as the Berezinskii-Kosterlitz-Thouless (BKT) transition [14–18]) at a finite Tc.
A realistic theoretical description of thin-film systems must include the exchange interaction, the dipolar interaction, and the on-site magneto-crystalline anisotropy, since the appearance of LRO in quasi 2d systems requires the breaking of the symmetry by magnetic anisotropy. The detailed nature of the magnetic anisotropy is determined by a subtle combination of magnetocrystalline interactions, due to the structure of the crystal or presence of a surface and the dipolar interaction which is inherently anisotropy. The dipolar interaction interaction which is often ignored (as the magnitude of the dipolar interaction is very small in comparison with respect to the exchange interaction) in theoretical studies of magnetic systems, plays an essential role in stabilizing LRO in 2d systems, as well as in determining the nature and morphology of ordered state. In addition to the inherent anisotropy of dipolar interaction, its long-range character is also important in determining the magnetic properties of low-dimensional systems. When the dipolar interaction and the anisotropy effects are considered along with the exchange interaction, the LRO can be established in planar Heisenberg systems [19,20]. Moreover, the competition between exchange, dipolar and anisotropy terms may cause heterogeneous magnetic phases like strip domain, canted phase or spin-vortex etc. [19, 20].
Before going to further detail of the 2d model systems let us have a glimpse over the behavior of a given system in the neighborhood of its critical point where phase transition occurs. Various physical quantities pertaining to the system possess singularities at the critical points. It is customary to express these singularities in terms of power laws characterized by a set of critical exponents which determine the qualitative nature of the critical behavior of the system. For magnetic systems, spontaneous magnetism, m (or the sub-lattice magnetization for antiferromagnets) is the order parameter and the applied magnetic field, h is the ordering field, so that when h → 0, m tends to a limiting value m0 = 0 (experiments often result in the remnant magnetization, mr(T) = m(h → 0, T), which might be different from m0(T) when magnetic domains are present) with the property that m0 = 0 for T ≥ Tc and 6= 0 for T < Tc. It is convenient, in the study of critical behavior, to work with reduced temperature, t = (T −Tc)/Tc. A critical exponent, β is defined for the manner in which m0 → 0, as T → Tc from below i.e. t → 0 −: m0 ∝ −tβ . The manner in which low-field susceptibility, χ0 diverges, as T → Tc from above (or below), defines the exponent, 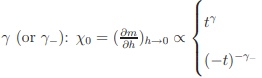 Another exponent, δ can be defined by the relation m(h, Tc) ∝ h 1/δ for h → 0 +. Two more exponents, α and ν, related with specific heat (ch) and correlation length (ξ), respectively, are defined as follows: ch ∝ t −α for t → 0+ and ξ ∝ t −ν for t → 0+.
Another exponent, δ can be defined by the relation m(h, Tc) ∝ h 1/δ for h → 0 +. Two more exponents, α and ν, related with specific heat (ch) and correlation length (ξ), respectively, are defined as follows: ch ∝ t −α for t → 0+ and ξ ∝ t −ν for t → 0+.
2d Ising model & 2d XY model
The 2d Ising model is an exactly solvable theoretical model (Onsager, 1944), exhibiting a spontaneous magnetization, m0(T) = m0(0) 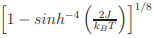 with a critical temperature kBTc/J ≈ 2.2. The asymptotic power law approximation results in a critical exponent, β = 1/8. For real systems with strong uniaxial anisotropy may be approximated to a 2d Ising like system and the critical exponents near the critical point can be compared with the theoretical values.
with a critical temperature kBTc/J ≈ 2.2. The asymptotic power law approximation results in a critical exponent, β = 1/8. For real systems with strong uniaxial anisotropy may be approximated to a 2d Ising like system and the critical exponents near the critical point can be compared with the theoretical values.
The 2d XY model has an interesting phase transition as T decreases, from the paramagnetic disordered phase to a phase which has no LRO but in which the magnetization on the plane has long-range correlations. This phase, described by Berezinskii-Kosterlitz and Thouless (BKT) [14–18] has topological defects in the form of vortices of the magnetization field which occur in tightly bound pairs that unbind at a critical temperature, given by Tc = πJ/kB. The susceptibility is infinite for all temperatures below Tc and finite above. The correlation function falls off algebraically at all finite temperatures following the relation g(r) ≈ exp 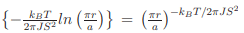 (where a is the lattice constant) and that there is no long-range order in the system. Despite the existence of a critical temperature, the 2d XY system of infinite size does not show a spontaneous magnetization. However, for every finite-sized 2d XY system in low temperature, the spin-spin correlation decays so slowly with distance that there exists a measurable spontaneous magnetization [16–18]. The renormalization group analysis shows that there is a regime of universal behavior near the BKT-transition temperature, TBKT with the magnetization obeying a power-law with a critical exponent β = 3π2 /128 ≈ 0.23. The finite size effects certainly play an important role in magnetic order, however, the their exact role in establishing LRO is not obvious.
(where a is the lattice constant) and that there is no long-range order in the system. Despite the existence of a critical temperature, the 2d XY system of infinite size does not show a spontaneous magnetization. However, for every finite-sized 2d XY system in low temperature, the spin-spin correlation decays so slowly with distance that there exists a measurable spontaneous magnetization [16–18]. The renormalization group analysis shows that there is a regime of universal behavior near the BKT-transition temperature, TBKT with the magnetization obeying a power-law with a critical exponent β = 3π2 /128 ≈ 0.23. The finite size effects certainly play an important role in magnetic order, however, the their exact role in establishing LRO is not obvious.
The critical exponents for 2d Ising and 2d-XY models are presented in the following table

Isotropic Heisenberg model in 2d
The possibility of LRO for isotropic Heisenberg system in low-dimensions can be tested following the Bloch’s treatment. One obtains the spin-wave (SW) or magnon dispersion relation, using the Holstein-Primakov transformation on diagonalize of the isotropic Heisenberg Hamiltonian as ω ∝ (1 − cos(ka)) i.e. ω ∝ k2 for ka << 1 (long wavelength approximation). Thus, the magnetization variation due to the thermal excitation of SW 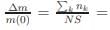
 and D(k) ∝ kd−1 , implying ∆m ∝ Td/2Γ(d/2)ζ(d/2) provided d/2 > 1, otherwise the Riemann-zeta function will diverge. So, for LRO we must have d > 2. Particularly, for d = 2, the magnetization diverges logarithmically at its lower bound, suggesting that the magnetization must be zero at finite temperature. (It may be noticed that the magnetization would have linear temperature dependence in 2d if SW excitations are allowed.)
and D(k) ∝ kd−1 , implying ∆m ∝ Td/2Γ(d/2)ζ(d/2) provided d/2 > 1, otherwise the Riemann-zeta function will diverge. So, for LRO we must have d > 2. Particularly, for d = 2, the magnetization diverges logarithmically at its lower bound, suggesting that the magnetization must be zero at finite temperature. (It may be noticed that the magnetization would have linear temperature dependence in 2d if SW excitations are allowed.)
However, the long-range dipolar interaction and/or anisotropy effect can establish the otherwise forbidden LRO in a planar Heisenberg system by introducing a low-energy cut-off, ∆ (function of dipolar field, Hd, anisotropy term, HK and/or exchange term, J) i.e. opening up a gap at the bottom of the spin-wave spectrum and the magnetization becomes finite
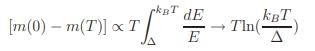
i.e.
m(T) = m(0)[1 − ATln(βT)] ...(1.1)
where A and β are constants. In case of an easy-plane system, ∆ is rather a pseudo-gap and ripple-like spin fluctuations are inevitable.
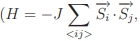 where J is the exchange integral and
where J is the exchange integral and 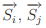 are the spins at i-th and j-th site, respectively), on the other hand, can show a variety of magnetic ordering depending upon the spin dimensionality, n and the space dimensionality, d. Exactly solvable 1d and 2d Ising (n=1) models have the transition temperature (below which an ordered state exists), Tc = 0 and a finite Tc, respectively, implying that 1d Ising system lacks long-range order (LRO) whereas spontaneous magnetization is expected for 2d Ising system at any finite temperature. The absence of LRO in 1d Ising model can be understood easily by considering the ex- citation of a 1d chain with free ends:
are the spins at i-th and j-th site, respectively), on the other hand, can show a variety of magnetic ordering depending upon the spin dimensionality, n and the space dimensionality, d. Exactly solvable 1d and 2d Ising (n=1) models have the transition temperature (below which an ordered state exists), Tc = 0 and a finite Tc, respectively, implying that 1d Ising system lacks long-range order (LRO) whereas spontaneous magnetization is expected for 2d Ising system at any finite temperature. The absence of LRO in 1d Ising model can be understood easily by considering the ex- citation of a 1d chain with free ends: 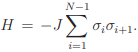 The excitation is nothing but the formation of a boundary (say, in-between i and i + 1-th site i.e. σi = 1 for i ≤ l, σi = −1 for i > l) between two different spinprojections which can occur in N − 1 ways. At any T ≠ 0, the change in free energy due to these excitations is 2J − kBTln(N − 1) which is less than zero for all T > 0 in the limit N → ∞. These excitations make the system disorder implying the expectation value of the magnetization to be zero. Therefore, there cannot be a phase transition to a ferromagnetic state in 1d Ising system with nearest-neighbor (or with any finite-range) interactions. If the Ising spins are placed on a 2d lattice, a phase transition to a magnetically ordered state below a non-zero critical temperature will result. This is because the energy cost and the entropy gain of making the boundary both scale with the perimeter size of the boundary. Energy and entropy therefore can have a fair fight with neither having an overwhelming advantage. Building on inequalities developed by Bogolubov and Hohenberg, the absence of LRO for isotropic, short-range interaction (more precisely, it must decrease more rapidly than 1/r3 ) in low-dimensions (d ≤ 2), is rigorously proved by Mermin and Wagner [13]. So for 2d XY (n=2) and 2d isotropic Heisenberg model (n=3) system no spontaneous magnetization is expected at any finite temperature. However, 2d XY (n=2) system is special to exhibit a continuous phase transition (known as the Berezinskii-Kosterlitz-Thouless (BKT) transition [14–18]) at a finite Tc.
The excitation is nothing but the formation of a boundary (say, in-between i and i + 1-th site i.e. σi = 1 for i ≤ l, σi = −1 for i > l) between two different spinprojections which can occur in N − 1 ways. At any T ≠ 0, the change in free energy due to these excitations is 2J − kBTln(N − 1) which is less than zero for all T > 0 in the limit N → ∞. These excitations make the system disorder implying the expectation value of the magnetization to be zero. Therefore, there cannot be a phase transition to a ferromagnetic state in 1d Ising system with nearest-neighbor (or with any finite-range) interactions. If the Ising spins are placed on a 2d lattice, a phase transition to a magnetically ordered state below a non-zero critical temperature will result. This is because the energy cost and the entropy gain of making the boundary both scale with the perimeter size of the boundary. Energy and entropy therefore can have a fair fight with neither having an overwhelming advantage. Building on inequalities developed by Bogolubov and Hohenberg, the absence of LRO for isotropic, short-range interaction (more precisely, it must decrease more rapidly than 1/r3 ) in low-dimensions (d ≤ 2), is rigorously proved by Mermin and Wagner [13]. So for 2d XY (n=2) and 2d isotropic Heisenberg model (n=3) system no spontaneous magnetization is expected at any finite temperature. However, 2d XY (n=2) system is special to exhibit a continuous phase transition (known as the Berezinskii-Kosterlitz-Thouless (BKT) transition [14–18]) at a finite Tc.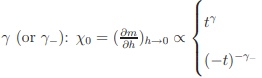 Another exponent, δ can be defined by the relation m(h, Tc) ∝ h 1/δ for h → 0 +. Two more exponents, α and ν, related with specific heat (ch) and correlation length (ξ), respectively, are defined as follows: ch ∝ t −α for t → 0+ and ξ ∝ t −ν for t → 0+.
Another exponent, δ can be defined by the relation m(h, Tc) ∝ h 1/δ for h → 0 +. Two more exponents, α and ν, related with specific heat (ch) and correlation length (ξ), respectively, are defined as follows: ch ∝ t −α for t → 0+ and ξ ∝ t −ν for t → 0+. 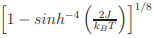 with a critical temperature kBTc/J ≈ 2.2. The asymptotic power law approximation results in a critical exponent, β = 1/8. For real systems with strong uniaxial anisotropy may be approximated to a 2d Ising like system and the critical exponents near the critical point can be compared with the theoretical values.
with a critical temperature kBTc/J ≈ 2.2. The asymptotic power law approximation results in a critical exponent, β = 1/8. For real systems with strong uniaxial anisotropy may be approximated to a 2d Ising like system and the critical exponents near the critical point can be compared with the theoretical values.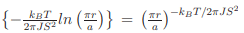 (where a is the lattice constant) and that there is no long-range order in the system. Despite the existence of a critical temperature, the 2d XY system of infinite size does not show a spontaneous magnetization. However, for every finite-sized 2d XY system in low temperature, the spin-spin correlation decays so slowly with distance that there exists a measurable spontaneous magnetization [16–18]. The renormalization group analysis shows that there is a regime of universal behavior near the BKT-transition temperature, TBKT with the magnetization obeying a power-law with a critical exponent β = 3π2 /128 ≈ 0.23. The finite size effects certainly play an important role in magnetic order, however, the their exact role in establishing LRO is not obvious.
(where a is the lattice constant) and that there is no long-range order in the system. Despite the existence of a critical temperature, the 2d XY system of infinite size does not show a spontaneous magnetization. However, for every finite-sized 2d XY system in low temperature, the spin-spin correlation decays so slowly with distance that there exists a measurable spontaneous magnetization [16–18]. The renormalization group analysis shows that there is a regime of universal behavior near the BKT-transition temperature, TBKT with the magnetization obeying a power-law with a critical exponent β = 3π2 /128 ≈ 0.23. The finite size effects certainly play an important role in magnetic order, however, the their exact role in establishing LRO is not obvious.
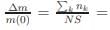
 and D(k) ∝ kd−1 , implying ∆m ∝ Td/2Γ(d/2)ζ(d/2) provided d/2 > 1, otherwise the Riemann-zeta function will diverge. So, for LRO we must have d > 2. Particularly, for d = 2, the magnetization diverges logarithmically at its lower bound, suggesting that the magnetization must be zero at finite temperature. (It may be noticed that the magnetization would have linear temperature dependence in 2d if SW excitations are allowed.)
and D(k) ∝ kd−1 , implying ∆m ∝ Td/2Γ(d/2)ζ(d/2) provided d/2 > 1, otherwise the Riemann-zeta function will diverge. So, for LRO we must have d > 2. Particularly, for d = 2, the magnetization diverges logarithmically at its lower bound, suggesting that the magnetization must be zero at finite temperature. (It may be noticed that the magnetization would have linear temperature dependence in 2d if SW excitations are allowed.)