Magnetostatics, Fundamentals | Basic Physics for IIT JAM PDF Download
Magnetostatics is the study of magnetic fields in systems where the currents are steady (not changing with time). It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that occur on time scales of nanoseconds or less.Magnetostatics is even a good approximation when the currents are not static — as long as the currents do not alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic storage devices as in computer memory. Magnetostatic focussing can be achieved either by a permanent magnet or by passing current through a coil of wire whose axis coincides with the beam axis.
Magnetostatics as a special case of Maxwell's equations
Starting from Maxwell's equations and assuming that charges are either fixed or move as a steady current J, the equations separate into two equations for the electric field (see electrostatics) and two for the magnetic field.The fields are independent of time and each other. The magnetostatic equations, in both differential and integral forms, are shown in the table below.
Where ∇ with the dot denotes divergence, and B is the magnetic flux density, the first integral is over a surface s with oriented surface element ds. Where ∇ with the cross denotes curl, J is the current density and H is the magnetic field intensity, the second integral is a line integral around a closed loop C with line element 1. The current going through the loop is Ienc.
The quality of this approximation may be guessed by comparing the above equations with the full version of Maxwell's equations and considering the importance of the terms that have been removed. Of particular significance is the comparison of the J term against the ∂D/∂t term. If the J term is substantially larger, then the smaller term may be ignored without significant loss of accuracy.
Re-introducing Faraday's law
A common technique is to solve a series of magnetostatic problems at incremental time steps and then use these solutions to approximate the term ∂B/∂t. Plugging this result into Faraday's Law finds a value for E (which had previously been ignored). This method is not a true solution of Maxwell's equations but can provide a good approximation for slowly changing fields.
Solving for the magnetic field
Current sources
If all currents in a system are known (i.e., if a complete description of the current density J (r)is available) then the magnetic field can be determined, at a position r, from the currents by the Biot–Savart equation: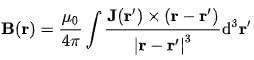
This technique works well for problems where the medium is a vacuum or air or some similar material with a relative permeability of 1. This includes air-core inductors and air-core transformers. One advantage of this technique is that, if a coil has a complex geometry, it can be divided into sections and the integral evaluated for each section. Since this equation is primarily used to solve linear problems, the contributions can be added. For a very difficult geometry, numerical integration may be used.
For problems where the dominant magnetic material is a highly permeable magnetic core with relatively small air gaps, a magnetic circuit approach is useful. When the air gaps are large in comparison to the magnetic circuit length, fringing becomes significant and usually requires a finite element calculation. The finite element calculation uses a modified form of the magnetostatic equations above in order to calculate magnetic potential. The value of B can be found from the magnetic potential.
The magnetic field can be derived from the vector potential. Since the divergence of the magnetic flux density is always zero,
B = ∇ x A
and the relation of the vector potential to current is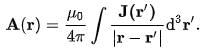
Magnetization
Strongly magnetic materials (i.e., ferromagnetic, ferrimagnetic or paramagnetic) have a magnetization that is primarily due to electron spin. In such materials the magnetization must be explicitly included using the relation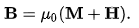
Except in metals, electric currents can be ignored. Then Ampère's law is simply
∇ x H = 0.
This has the general solution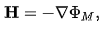
where ФM is a scalar potential.Substituting this in Gauss's law gives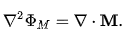
Thus, the divergence of the magnetization, ∇.M, has a role analogous to the electric charge in electrostatics and is often referred to as an effective charge density ρM.
The vector potential method can also be employed with an effective current density.
|
214 videos|156 docs|94 tests
|
FAQs on Magnetostatics, Fundamentals - Basic Physics for IIT JAM
| 1. What is magnetostatics? |  |
| 2. What are the fundamentals of magnetostatics? |  |
| 3. How is magnetostatics different from electromagnetism? |  |
| 4. What are some practical applications of magnetostatics? |  |
| 5. How can magnetostatics be used to calculate magnetic fields? |  |
















