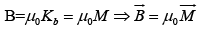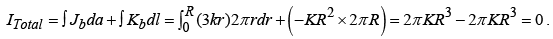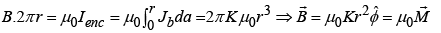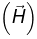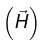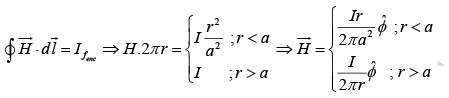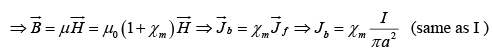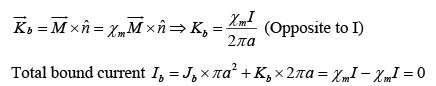Magnetostatics | Electricity & Magnetism - Physics PDF Download
Magnetic Force on Current
The magnetic field at any point due to steady current is called a magnetostatic field. The magnetic force on a charge Q , moving with velocity v in a magnetic field 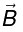 is,
is, 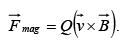 This is known as Lorentz force law.
This is known as Lorentz force law.
In the presence of both electric and magnetic fields, the net force on Q would be: 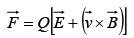
Current in a Wire
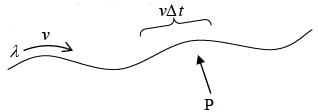
A line charge λ traveling down a wire at a speed 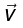 constitutes a current
constitutes a current 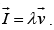
Magnetic force on a segment of current-carrying wire is,
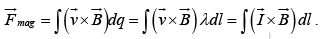
since 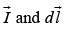 points in the same direction
points in the same direction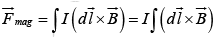
Surface Current Density
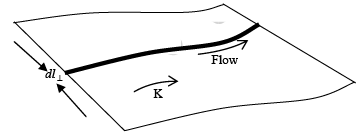
When charge flows over a surface, we describe it by the surface current 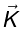
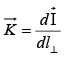 is the current per unit width-perpendicular to flow.
is the current per unit width-perpendicular to flow.
Also 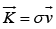 where is σ surface charge density and
where is σ surface charge density and 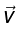 is its velocity.
is its velocity.
Magnetic force on surface current 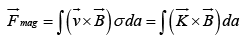
Volume Current Density
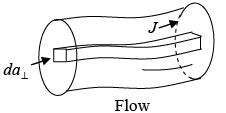
When the flow of charge is distributed throughout a three-dimensional region, we describe it by the volume current density 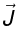 .
.
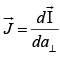 is the current per unit area-perpendicular to flow.
is the current per unit area-perpendicular to flow.
Also 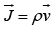 where ρ is volume charge density and
where ρ is volume charge density and 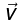 is its velocity.
is its velocity.
Magnetic force on volume current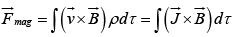
Current crossing a surface S is 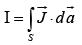
Example 1: A wire ABCDEF (with each of side of length L ) bent as shown in figure and carrying a current I is placed in a uniform magnetic induction B parallel to the positive y-direction. Find the force experienced by the wire.
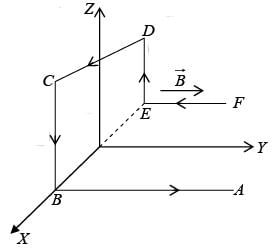
FE and BA are parallel to magnetic induction
. Magnetic force on each of them will be zero. DE and CB are perpendicular to
. They carry currents in opposite directions forces on them will be equal in magnitude and opposite in direction. The net force due to these portions of wire will be zero. Now force on side DC is
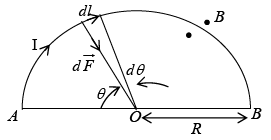
Example 2: A semi–circular wire of radius R carries a current I and is placed in a uniform field B acting perpendicular to the plane of the semi–circle. Calculate force acting on the wire.
Consider an element of length dl of the wire. The
force on this element is obtained by
(Horizontal component cancels only perpendicular component add up).
Continuity Equation
The total charge per unit time leaving a volume V is 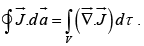
Because charge is conserved, whatever flows out through the surface must come at the expense of that remaining inside: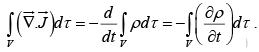
(The minus sign reflects the fact that an outward flow decreases the charge left in V.) Since this applies to any volume, we conclude that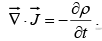
This is the precise mathematical statements of local charge conservation.
Note: When a steady current flows in a wire, its magnitude I must be the same all along the line; otherwise, charge would be piling up somewhere, and it wouldn't be a steady current. Thus for magnetostatic fields 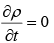 and hence the continuity equation becomes:
and hence the continuity equation becomes: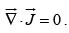
Biot-Savart Law
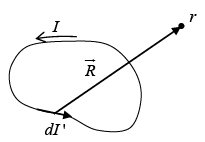
The magnetic field of a steady line current is given by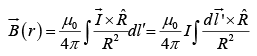
where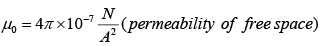
For surface and volume current Biot-Savart law becomes: 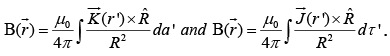
Magnetic Field due to Wire
Let us find the magnetic field a distance d from a long straight wire carrying a steady current I.
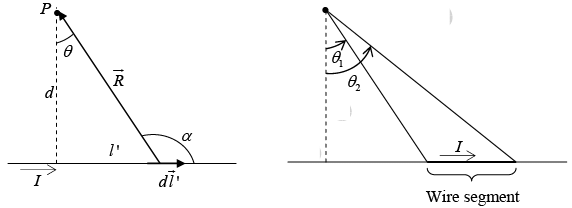
In the diagram, 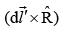 points out of the page and has magnitude dl′ sinα = dl′cos θ
points out of the page and has magnitude dl′ sinα = dl′cos θ
Since,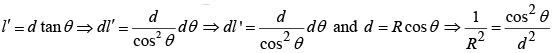
From Biot–Savart law: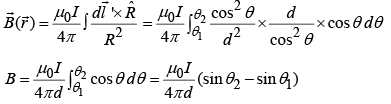
For Infinite wire: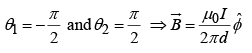
Note:
- Magnetic field a distance r from a long straight wire carrying a steady current I is

- Magnetic field a distance r from a infinite wire carrying a steady current I is:

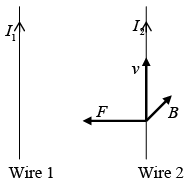
- Force (per unit length) of attraction between two long, parallel wires a distance d apart, carrying currents I1 and I2 in same direction are:

- If currents are in opposite direction they will repel with same magnitude.
Magnetic Field due to Solenoid and Toroid
The magnetic field of a very long solenoid, consisting of n closely wound turns per unit length of a cylinder of radius R and carrying a steady current I is:

Magnetic field due to Toroid is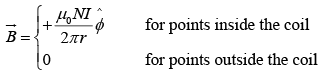
where N is the total number of turns.
Example 3: Find the force of attraction between two long, parallel wires a distance d apart, carrying current I1 and I2 in the same direction.
The field at (2) due to (1) is
Force on (2) is
Force per unit length is towards (1) and net force is attractive.
Example 4: Find the magnetic field a distance d above the center of a circular loop of radius R, which carries a steady current I.
The field
attributable to the segment
as shown. As we integrate

around the loop,
sweeps out a cone. The horizontal components cancel, and the vertical components combine to give.
Example 5: Find the force on a square loop placed as shown in figure, near an infinite straight wire. Both the loop and the wire carry a steady current I.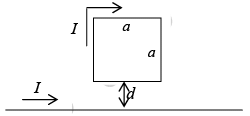
The force on the two sides cancels.
At the bottom,
At the top,
Thus
Ampere's Law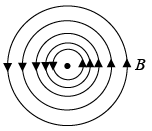
The magnetic field of an infinite wire is shown in the figure (the current is coming out of the page). Let us find the integral of  around a circular path of radius r, centered at the wire, is
around a circular path of radius r, centered at the wire, is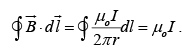
Notice that the answer is independent of r; that is because B decreases at the same rate as the circumference increases. If we use cylindrical coordinates ( r ,φ,z ) , with the current flowing along the z axis,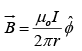
In general we can write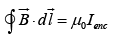
where Ienc is the total current enclosed by the amperian loop.
since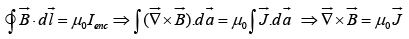
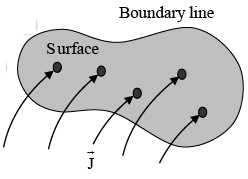
Right hand Rule
If the fingers of your right hand indicate the direction of integration around the boundary, then your thumb defines the direction of a positive current.
Example 6: A steady current I flow down a long cylindrical wire of radius a. Find the magnetic field, both inside and outside the wire, if
- The current is uniformly distributed over the outside surface of the wire.
- The current is distributed in such a way that J is proportion to r, the distance from the axis.
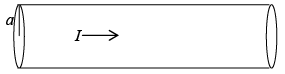
(1)
(2)
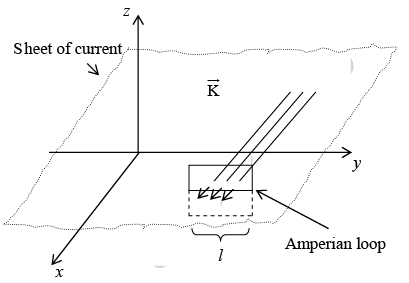
Example 7: Find the magnetic field of an infinite uniform surface current 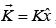 , flowing over the x–y plane.
, flowing over the x–y plane.
Since
have no x-component because B is ⊥r to x-component i.e. in the direction of
Also,have no z-component: For y > 0 , B is along
and for y < 0 , B is along −
thus field cancels each other.
⇒
has only y-component:
For z >0 ,
points left (
) and for z <0 ,
point’s right (
).
Draw a rectangular amperian loop parallel to the yz plane and extending an equal distance above and below the surface. Now apply ampere’s law, we find
{One Bl from top segment, and the other from bottom}
Note: The field is independent of the distance from the plane, just like the electric field of a uniform surface charge.
Magnetic Vector Potential 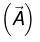
Since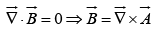
For magnetostatic fields,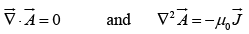
if 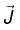 goes to zero at infinity,
goes to zero at infinity, 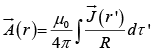 for volume current.
for volume current.
For line and surface currents,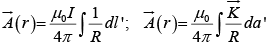
Example 8: What current density would produce the vector potential 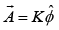 (where K is a constant), in cylindrical coordinates ?
(where K is a constant), in cylindrical coordinates ?
Magnetostatic Boundary Condition (Boundary is sheet of current, 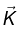 )
)
Just as the electric field suffers a discontinuity at a surface charge, so the magnetic field is discontinuous at a surface current. Only this time it is the tangential component that changes.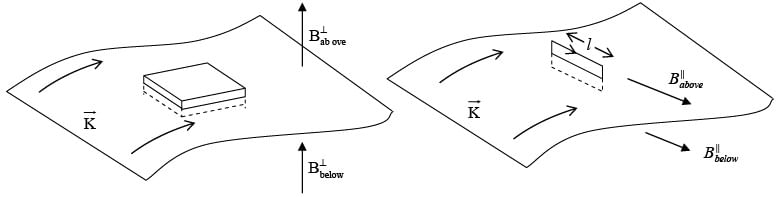
Since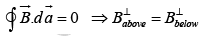
For tangential components
Thus the component of 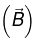 that is parallel to the surface but perpendicular to the current is discontinuous in the amount μ0K . A similar amperian loop running parallel to the current reveals that the parallel component is continuous. The result can be summarized in a single formula:
that is parallel to the surface but perpendicular to the current is discontinuous in the amount μ0K . A similar amperian loop running parallel to the current reveals that the parallel component is continuous. The result can be summarized in a single formula:
where 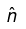 is a unit vector perpendicular to the surface, pointing “upward”. Like the scalar potential in electrostatics, the vector potential is continuous across, a boundary:
is a unit vector perpendicular to the surface, pointing “upward”. Like the scalar potential in electrostatics, the vector potential is continuous across, a boundary: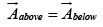
For 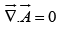 guarantees that the normal component is continuous, and
guarantees that the normal component is continuous, and
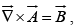 in the form
in the form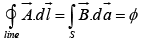
But the derivative of 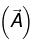 inherits the discontinuity of
inherits the discontinuity of 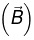

Example 9: (a) Find the magnetic vector potential at a distance r from an infinite straight wire carrying a current I.
(b) Find the magnetic potential inside the wire, if it has radius R and the current is uniformly distributed.
(a)
point in the same direction as I and is a function of r (the distance from the wire). In cylindrical coordinates
(b)
where b is arbitrary constant.must be continuous at R,

which means that we must pick a and b such that
Example 10: Find the vector potential of an infinite solenoid with n turns per unit length, radius R, and current I.
Since
where φ is the flux of
through the loop in question.
Inside solenoid:
Outside solenoid:
Multiple Expansion of Vector Potential
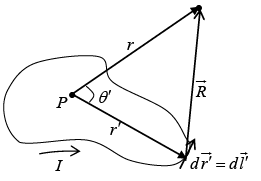
We can derive approximate formula for the vector potential of a localized current distribution, valid at distant points. We can always write the potential in the form of a power series in 1/r, where r is the distance to the point in question. Thus we can always write
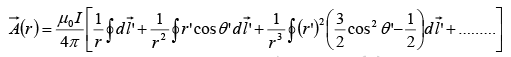
First term, monopole 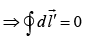 (no magnetic monopole)
(no magnetic monopole)
Second term, dipole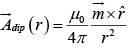
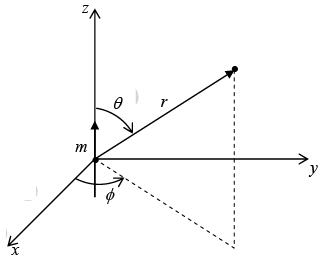
where 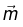 is the magnetic dipole moment:
is the magnetic dipole moment: 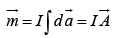
where 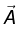 is area vector
is area vector
Thus
Hence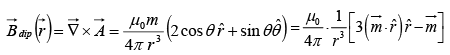
Note: (a) When a magnetic dipole is placed in a uniform magnetic field 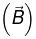
net force on the dipole is zero and it experiences a torque 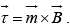
(b) In non-uniform field, dipoles have net force 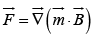 and torque
and torque
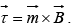
(c) Energy of an ideal dipole 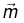 in an magnetic field
in an magnetic field 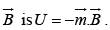
(d) Interaction energy of two dipoles separated by a distance 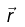 is
is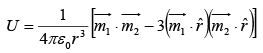
Example 11: A phonograph record of radius R, carrying a uniform surface charge σ is rotating at constant angular velocity ω. Find its magnetic dipole moment.
Magnetic moment of a ring of radius r and thickness dr is, dm = Iπr2 where
I = σvdr= σrωdr
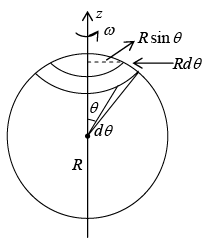
Example 12: A spherical shell of radius R, carrying a uniform surface charge σ, is set spinning at angular velocity ω. Find its Magnetic dipole moment.
The total charge on the shaded ring is
dq = σ (2π R sinθ ) Rdθ
Time for one revolution is
⇒Current in the ring
Area of the ring =π(R sin θ)2 , so the magnetic moment of the ring is
Magnetisation 
If a piece of magnetic material is examined on an atomic scale we will find tiny currents: electrons orbiting around nuclei and electrons spinning about their axes. For macroscopic purpose, these current loops are so small that we may treat them as magnetic dipoles. Ordinarily they cancel each other out because of the random orientation of the atoms. But when a magnetic field is applied, a net alignment of these magnetic dipoles occurs, and medium becomes magnetically polarized, or magnetized.
Magnetization  is magnetic dipole moment per unit volume.
is magnetic dipole moment per unit volume.
The Field of a Magnetized Object (Bound Currents)
Consider a piece of magnetized material with magnetization 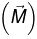
Then the vector potential of a single dipole 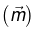 is given by
is given by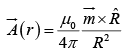
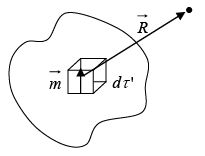
In the magnetized object, each volume element dτ ′ carries a dipole moment 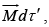 so the total vector potential is
so the total vector potential is
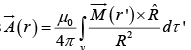
The equation can be written as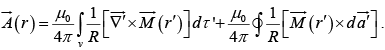
The first term is like potential of a volume current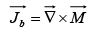
while the second term is like potential of a surface current,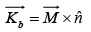
where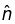 is the normal to the unit vector. With these definitions, the field of a magnetized object is
is the normal to the unit vector. With these definitions, the field of a magnetized object is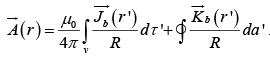
This means the potential(and hence also the field) of a magnetized object is the same as would be produced by a volume current 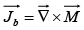 throughout the material, plus a surface current
throughout the material, plus a surface current 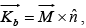 on the boundary. We first determine these bound currents, and then find the field they produce.
on the boundary. We first determine these bound currents, and then find the field they produce.
Example 13: An infinitely long circular cylinder carries a uniform magnetization 
parallel to its axis. Find the magnetic field (due to 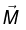 ) inside and outside the cylinder.
) inside and outside the cylinder.

The field is that of a surface current
that is the case of a solenoid,
So the field outside is zero.
Field inside is:

Example 14: A long circular cylinder of radius R carries a magnetization 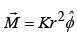
where K is a constant; r is the distance from the axis. Find the magnetic field due to
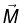 for points inside and outside the cylinder.
for points inside and outside the cylinder.
So the bound current flows up the cylinder, and returns down the surface.
Outside point: Ienc = 0⇒B =0
Inside point:
The Auxiliary field 
Ampere’s Law in in presence of Magnetic Materials In a magnetized material the total current can be written as 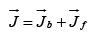 where
where 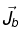 is bound current and
is bound current and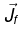 is free current.
is free current.
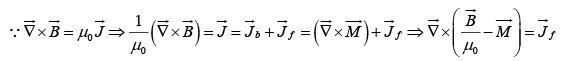
The quantity in parentheses is designated by the letter 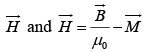

In integral form 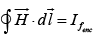 where
where 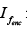 is the total free current passing through the amperian loop.
is the total free current passing through the amperian loop.
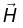 plays a role in magnetostatic analogous to
plays a role in magnetostatic analogous to 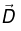 in electrostatic: Just as
in electrostatic: Just as 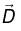
allowed us to write Gauss's law in terms of the free charge alone, 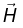 permits us to express Ampere's law in terms of the free current alone- and free current is what we control directly. Note: When we have to find
permits us to express Ampere's law in terms of the free current alone- and free current is what we control directly. Note: When we have to find  or
or 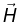 in a problem involving magnetic materials, first look for symmetry. If the problem exhibits cylindrical, plane, solenoid, or toroidal symmetry, then we can get
in a problem involving magnetic materials, first look for symmetry. If the problem exhibits cylindrical, plane, solenoid, or toroidal symmetry, then we can get 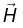 directly from the equation
directly from the equation 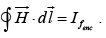
Magnetic Susceptibility and Permeability
For most substances magnetization is proportional to the field 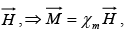 where χm is magnetic susceptibility of the material.
where χm is magnetic susceptibility of the material.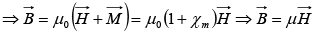 where(μ = μ0μr= μ0(1 + χm) is permeability
where(μ = μ0μr= μ0(1 + χm) is permeability
of material.
Boundary Condition 
The boundary between two medium is a thin sheet of free surface current Kf . The Ampere’s law states that
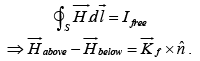
Since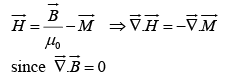
Thus

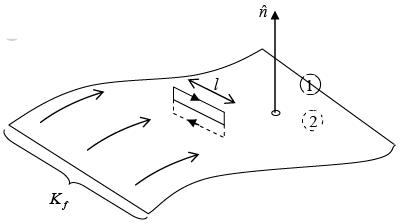
Example 15: A current I flows down a long straight wire of radius a. If the wire is made of linear material with susceptibility χm , and the current is distributed uniformly, what is the magnetic field a distance r from the axis? Find all the bound currents. What is the net bound current following down the wire?
|
82 videos|32 docs|22 tests
|
FAQs on Magnetostatics - Electricity & Magnetism - Physics
| 1. What is magnetostatics? |  |
| 2. How is magnetostatics different from electromagnetism? |  |
| 3. What are some applications of magnetostatics? |  |
| 4. What is Gauss's law for magnetism? |  |
| 5. How does Ampere's law relate to magnetostatics? |  |

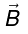 . Magnetic force on each of them will be zero. DE and CB are perpendicular to
. Magnetic force on each of them will be zero. DE and CB are perpendicular to 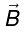 . They carry currents in opposite directions forces on them will be equal in magnitude and opposite in direction. The net force due to these portions of wire will be zero. Now force on side DC is
. They carry currents in opposite directions forces on them will be equal in magnitude and opposite in direction. The net force due to these portions of wire will be zero. Now force on side DC is 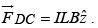
 Consider an element of length dl of the wire. The
Consider an element of length dl of the wire. The  force on this element is obtained by
force on this element is obtained by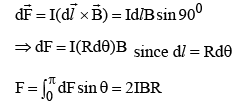
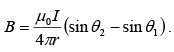
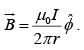
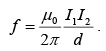
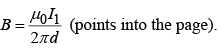
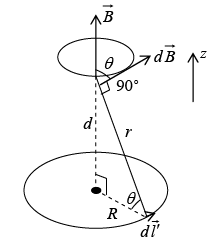
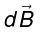 attributable to the segment
attributable to the segment 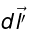 as shown. As we integrate
as shown. As we integrate 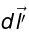
 sweeps out a cone. The horizontal components cancel, and the vertical components combine to give.
sweeps out a cone. The horizontal components cancel, and the vertical components combine to give.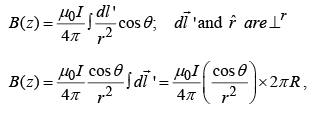

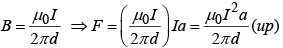

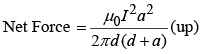
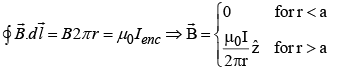
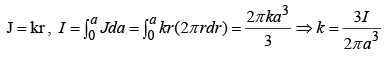
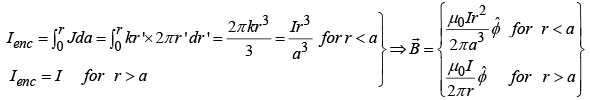
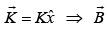 have no x-component because B is ⊥r to x-component i.e. in the direction of
have no x-component because B is ⊥r to x-component i.e. in the direction of 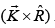
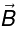 have no z-component: For y > 0 , B is along
have no z-component: For y > 0 , B is along 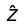 and for y < 0 , B is along −
and for y < 0 , B is along −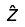 thus field cancels each other.
thus field cancels each other.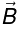 has only y-component:
has only y-component: 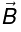 points left (
points left (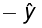 ) and for z <0 ,
) and for z <0 , 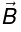 point’s right (
point’s right ( ).
).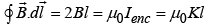 {One Bl from top segment, and the other from bottom}
{One Bl from top segment, and the other from bottom}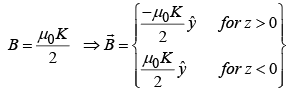
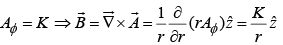
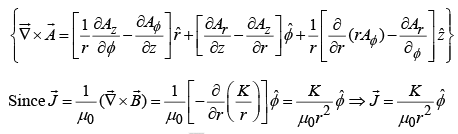
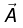 point in the same direction as I and is a function of r (the distance from the wire). In cylindrical coordinates
point in the same direction as I and is a function of r (the distance from the wire). In cylindrical coordinates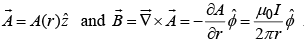
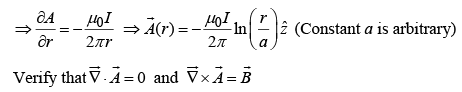
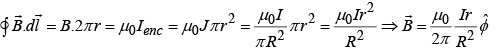
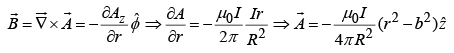
 must be continuous at R,
must be continuous at R, 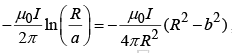
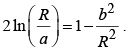
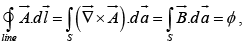 where φ is the flux of
where φ is the flux of 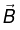 through the loop in question.
through the loop in question.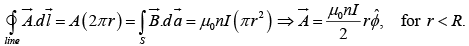
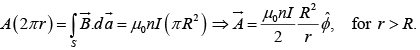
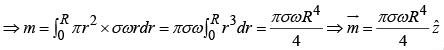
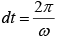
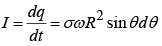
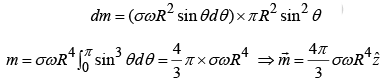
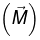
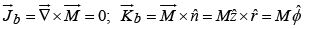
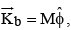 that is the case of a solenoid,
that is the case of a solenoid,