Mass Spring Damper System | Theory of Machines (TOM) - Mechanical Engineering PDF Download
Introduction
The most basic system that is used as a model for vibrational analysis is a block of mass m connected to a linear spring (with spring constant K and unstretched length ℓ0) and a viscous damper (with damping coefficient c). In addition, an external force P(t) is applied to the block and the displacement of the block is measured from the inertially fixed point O, where O is the point where the spring is unstretched. Finally, the spring and damper are both attached at the inertially fixed point Q. This system is shown in Fig. 1–1 Denoting unit vector in the direction from O to Q as Ex and the inertial reference frame of the ground by F, the inertial acceleration of the block is given as
Fa = x¨Ex (1–1)
Next, the forces exerted by the spring and damper are given, respectively, as
Fs = −K(ℓ − ℓ0)us (1–2)
Ff = −cvrel (1–3)
First, because the spring is attached at point Q, we have
ℓ = ║ r − rQ ║ (1–4)

Figure 1–1 Block of mass m sliding without friction along a horizontal surface connected to a linear spring and a linear viscous damper.
where r and rQ are the positions of the block and the attachment points of the spring, respectively. Using a coordinate system with its origin at point O at Ex as the first principal direction, we have
r = xEx (1–5)
rQ = ℓ0Ex (1–6)
Therefore,

Then, because x < ℓ0 we have
|x − ℓ0| = ℓ0 − x (1–8)
Finally, the unit vector in the direction from the attachment point of the spring to the position of the block is

The force in the linear spring is then given as

Next, because the ground is already assumed to be inertial, the relative velocity between the block and the ground is simply the velocity of the block, i.e., (1–11)
(1–11)
Therefore, the force exerted by the viscous damper is obtained as
 (1–12)
(1–12)
The resultant external force acting on the particle is then obtained as
 (1–13)
(1–13)
Applying Newton’s second law to the particle, we obtain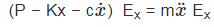 (1–14)
(1–14)
Dropping Ex from Eq. (1–14) and rearranging, we obtain the differential equation of motion as
 (1–15)
(1–15)
Now historically it has been the case that the differential equation has been written in a form that is normalized by the mass, i.e., we divide Eq. (1–15) by m to obtain

where p(t) = P (t)/m. Furthermore, it is common practice to define the quantities K/m and c/m as follows:
The quantities ωn and ζ are called the natural frequency and damping ratio of the system, respectively. In terms of the natural frequency and damping ratio, the differential equation of motion for the mass-spring-damper system can be written in the so-called standard form as
It is seen that Eq. (1–17) is a second-order linear constant coefficient ordinary differential equation. Often, the term “constant coefficient” is replaced with the term time-invariant, i.e., we say that Eq. (1–17) is called a second-order linear time-invariant (LTI) ordinary differential equation. The terminology “time-invariant” stems from the fact that for a given input p(t) and a given set of initial conditions  at the initial time t = t0 is the same as the solution to the input p(t + τ) for the initial conditions
at the initial time t = t0 is the same as the solution to the input p(t + τ) for the initial conditions  at the (shifted) initial time t = t0 + τ. Because of this fact associated with an LTI system, without loss of generality, we can assume that the initial time is zero, i.e., t0 = 0. Thus, when studying the zero input response of an LTI system we can restrict our attention to initial conditions
at the (shifted) initial time t = t0 + τ. Because of this fact associated with an LTI system, without loss of generality, we can assume that the initial time is zero, i.e., t0 = 0. Thus, when studying the zero input response of an LTI system we can restrict our attention to initial conditions  .
.
General Solution of a Second-Order LTI Differential Equation
Eq. (1–17) can be written as

which can be further written as
Now let

Then we can view the system of Eq. (1–17) as a system of the form
Lx = f (1–21)
It is seen that the operator L defined in Eq. (1–20) is linear because
L(αx1 + βx2) = αL(x1) + βL(x2) (1–22)
for all constants α and β. Then it is seen that Eq. (1–21) is a linear system whose general solution is of then form Eq. (1–17) is given as
x(t) = xh(t) + xp(t) (1–23)
here xh(t) is the homogeneous solution (i.e., the solution for a particular set of initial conditions  with a zero input function p(t) ≡ 0) while xp(t) is the particular solution (i.e., the solution for zero initial conditions (x(t0), x(t0) = (0, 0) and an arbitrary input function p(t) ≠ 0). The homogeneous solution and particular solutions are also called the zero input response and zero initial condition response, respectively. The general solution x(t) to a second-order LTI system is then given as the sum of the zero input response and the zero initial condition response. Because the zero input response satisfies Eq. (1–17) when p(t) ≡ 0, we have
with a zero input function p(t) ≡ 0) while xp(t) is the particular solution (i.e., the solution for zero initial conditions (x(t0), x(t0) = (0, 0) and an arbitrary input function p(t) ≠ 0). The homogeneous solution and particular solutions are also called the zero input response and zero initial condition response, respectively. The general solution x(t) to a second-order LTI system is then given as the sum of the zero input response and the zero initial condition response. Because the zero input response satisfies Eq. (1–17) when p(t) ≡ 0, we have

Contrariwise, because the zero initial condition response satisfies Eq. (1–17) when p(t) ≠ 0 and the initial conditions are zero, we have

From the preceding discussion, it is seen that studying the general response of a second-order LTI system amounts to studying independently the zero input response and the zero initial condition response. Consequently, the study of single-degree-of-freedom vibrations amounts to quantifying the zero input response and the zero initial condition response. In the remainder of this chapter, we study in detail the zero input response of a second-order LTI system that arises in the study of mechanical vibrations.
|
87 videos|43 docs|29 tests
|
FAQs on Mass Spring Damper System - Theory of Machines (TOM) - Mechanical Engineering
| 1. What is a second-order LTI differential equation? |  |
| 2. What is a mass spring damper system? |  |
| 3. How is the general solution of a second-order LTI differential equation derived for a mass spring damper system? |  |
| 4. What are the physical interpretations of the parameters in a mass spring damper system? |  |
| 5. How does the behavior of a mass spring damper system change with different parameter values? |  |



















