Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Mathematical Operations
Mathematical Operations | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Mathematical Symbols
What mathematical symbols do I need to know?
- Starting with the basic four operations
+ Addition, plus, sum, total
- Subtraction, minus, difference, take away
x Multiplication, product, times
÷ Division, quotient, divide, share - Equals signs
= Equal to e.g. 3 x + 7 = 19
≠ Not equal to e.g.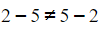
≈ Approximately equal to e.g. π ≈ 3.14
≡ Identical to e.g. 12 x + 6 ≡ 3 (4 x + 2) - Inequality signs
> Greater than e.g. 5 > - 2
< Less than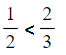
≥ Greater than or equal to
≤ Less than or equal to - Other helpful symbols
() Brackets: used to group symbols e.g.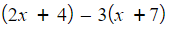
3 x Powers (also called indices, order or exponents): repeated multiplication of the base number
e.g. 34 = 3 x 3 x 3 x 3 = 81
√ Square root: opposite of squaring e.g.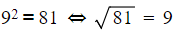
± Plus Minus: Used to allow for two distinct answers, often in quadratics
a ± b is shorthand for a + b and a - b
e.g. x = 3 ± 2.5 leading to x = 5.5 and x = 0.5
π Pi: the ratio of the circumference of a circle to its diameter
Order of Operations (BIDMAS/BODMAS)
What is the order of operations (BIDMAS/BODMAS)?
- If there are multiple operations then they must be done in the following order:
- Brackets: ( )
- Perform the calculation(s) inside any brackets first
- Indices or Order: ˄, 2, 3, √, etc
- These include powers, roots, reciprocals
- Divisions or Multiplications: × or ÷
- If there are more than one of these then work them out left to right
- Additions or Subtractions: + or -
- If there are more than one of these then work them out left to right
- Brackets: ( )
- The acronyms BIDMAS and BODMAS can help you remember
What do I do if the calculation involves fractions, powers or roots?
For fractions there are invisible brackets around the numerator and around the denominator
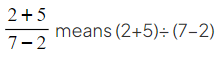
- Instead of using brackets we extend the fraction line to show exactly what is on the top and what is on the bottom
For powers there are invisible brackets around the power
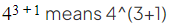
- Instead of using brackets we write the whole to the right of the number and raised
For roots there are invisible brackets under the root
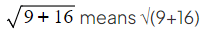
- Instead of using brackets we extend the line on the root symbol to show exactly what is being rooted
The document Mathematical Operations | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Mathematical Operations - Mathematics for GCSE/IGCSE - Class 10
| 1. What does BIDMAS/BODMAS stand for? |  |
Ans. BIDMAS/BODMAS stands for Brackets, Indices (or Orders), Division and Multiplication (left-to-right), Addition and Subtraction (left-to-right). It is an acronym used to remember the order of operations in mathematics.
| 2. Why is it important to follow the order of operations in mathematical calculations? |  |
Ans. Following the order of operations ensures that mathematical expressions are evaluated correctly and consistently. If the order is not followed, the result of a calculation may be incorrect.
| 3. How do you apply the order of operations when solving a mathematical expression? |  |
Ans. To apply the order of operations, you must perform operations inside parentheses or brackets first, then evaluate any exponents or roots, followed by multiplication and division from left to right, and finally addition and subtraction from left to right.
| 4. Can you provide an example of how the order of operations works in a mathematical expression? |  |
Ans. For example, in the expression 3 + 2 x 4, you would first multiply 2 by 4 to get 8, then add 3 to get a final result of 11. If you were to add 3 and 2 first, the result would be 10, which is incorrect.
| 5. Why is it important to use parentheses or brackets in mathematical expressions? |  |
Ans. Parentheses or brackets are used to indicate which operations should be performed first, overriding the normal order of operations. They help clarify the intended meaning of an expression and ensure that calculations are carried out correctly.
Related Searches
















