Maths Olympiad Model Test Paper -3 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: If ‘P × Q’ means ‘P is brother of Q’,
‘P – Q’ means ‘P is sister of Q’,
‘P + Q’ means ‘P is father of Q’,
‘P ÷ Q’ means ‘P is mother of Q’,
then how is A related to D in B + A ÷ C – D?
(a) Aunt
(b) Niece
(c) Mother
(d) Can't be determined
 View Answer
View Answer 
Ans: (c)
- In the expression B + A ÷ C – D:
- B + A indicates that B is the father of A.
- A ÷ C shows that A is the mother of C.
- C – D means that C is the sister of D.
- Thus, A is the mother of C, and since C is D's sister, A is also the mother of D.
Q2: Find the water image of the given figure.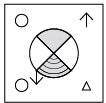 (a)
(a) 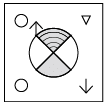
(b) 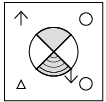
(c) 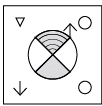
(d) 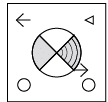
 View Answer
View Answer 
Ans: (a)
Q3: There is a definite relationship between figures (i) and (ii). Establish a similar relationship between figures (iii) and (iv) by selecting a suitable figure from the options that would replace the (?) in fig. (iv).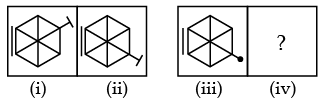 (a)
(a) 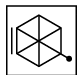
(b) 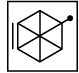
(c) 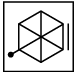
(d) 
 View Answer
View Answer 
Ans: (b)
Q4: Two sequences of numbers are provided. You need to calculate the resulting number for each sequence using the specified rules, and then answer the question that follows. The calculations for each sequence are performed from left to right.
(a) 57
(b) 72
(c) 69
(d) 65
 View Answer
View Answer 
Ans: (c)
- In the first row, the numbers are 48, 12, and 253. The operations are performed from left to right.
- First, divide 48 by 12, which gives 4.
- Next, multiply 4 by 253, resulting in 1012. This is the resultant number for the first row.
- For the second row, the operations are similar. You need to apply the same rules to find the resultant number.
- After performing the calculations, the resultant number for the second row is found to be 69.
Q5: Which number will replace the question mark in the figure below?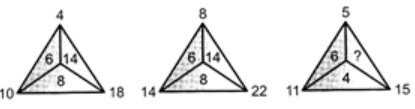 (a) 6
(a) 6
(b) 8
(c) 10
(d) 14
 View Answer
View Answer 
Ans: (c)
Q6: Find the missing number which replaces the (?) in the following.
(a) 35
(b) 40
(c) 49
(d) 53
 View Answer
View Answer 
Ans: (b)
Q7: The average of 9 numbers is 24. If the average of first 4 numbers is 32 and that of last 4 is 29, then find the 5th number.
(a) -27
(b) -28
(c) -29
(d) -30
 View Answer
View Answer 
Ans: (b)
Q8: In the given Venn diagram, ‘circle’ represents ‘married people’, ‘triangle’ represents ‘graduates’ and ‘square’ represents ‘poets’. How many married poets are there who are not graduates?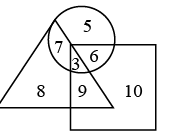 (A) 9
(A) 9
(B) 6
(C) 3
(D) 7
 View Answer
View Answer 
Ans: (b)
Number of married poets who are not graduates is 6.
Q9: B, D, M, K, P, Q, W and H are sitting around a circle facing at the centre. M is to the immediate right of B who is fourth to the right of K. P is second to the left of B and is fourth to the right of W. Q is second to the right of D who is second to the right of H. Which of the following represents the immediate neighbours of D?
(a) PQ
(b) KQ
(c) PH
(d) PK
 View Answer
View Answer 
Ans: (d)
The correct sitting arrangement is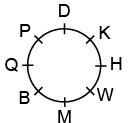 So, P and K are the immediate neighbours of D.
So, P and K are the immediate neighbours of D.
Q10: Select a figure from the options which when placed in the blank space of given figure would complete the pattern.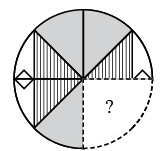 (a)
(a) 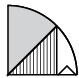
(b) 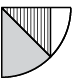
(c) 
(d) 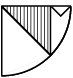
 View Answer
View Answer 
Ans: (c)
Q11: A machine that rearranges words and numbers follows specific rules for each step. Given the input line of words and numbers, identify the last step for the new input based on the previous example. Input: jockey firm 36 43 growth chart 22 45
(a) Step V
(b) Step VI
(c) Step IV
(d) Step VII
 View Answer
View Answer 
Ans: (a)
- The input consists of words and numbers: jockey, firm, 36, 43, growth, chart, 22, 45.
- Following the pattern from the previous example, the machine prioritizes numbers first, then words in alphabetical order.
- In the first step, the highest number is moved to the front, followed by the next highest, and so on.
- After several steps, the final arrangement will be similar to Step V from the previous example, which is the last step for this input.
Q12: A word and number arrangement machine when given an input line of words and numbers, rearranges them following a particular rule in each step. The following is an illustration of input and steps of rearrangement.
Input : 56 dress fine shine 32 66 72 offer
Step I : 72 56 dress fine shine 32 66 offer
Step II : 72 shine 56 dress fine 32 66 offer
Step III : 72 shine 66 56 dress fine 32 offer
Step IV : 72 shine 66 offer 56 dress fine 32
Step V : 72 shine 66 offer 56 fine dress 32
Step VI : 72 shine 66 offer 56 fine 32 dress
Step VI is the last step of the given arrangement. As per the rules followed in above steps, find the last step for the given below input.
Input : jockey firm 36 43 growth chart 22 45
(a) Step V
(b) Step VI
(c) Step IV
(d) Step VII
 View Answer
View Answer 
Ans: (a)
Input : jockey firm 36 43 growth chart 22 45
Step I : 45 jockey firm 36 43 growth chart 22
Step II : 45 jockey 43 firm 36 growth chart 22
Step III : 45 jockey 43 growth firm 36 chart 22
Step IV : 45 jockey 43 growth 36 firm chart 22
Step V : 45 jockey 43 growth 36 firm 22 chart
Q13: How many pairs of letters are there in the word SPONTANEOUS each of which have as many letters between them in the word as in the English alphabet?
(a) None
(b) Two
(c) Three
(d) More than three
 View Answer
View Answer 
Ans: (c)
Q14: How many 9’s are present in the given sequence that are not preceded by 5 and are immediately followed by either 2 or 3?
(a) One
(b) Three
(c) Five
(d) Six
 View Answer
View Answer 
Ans: (b)
- To find the count of 9’s that meet the criteria, we need to look for 9’s that are not preceded by a 5 and are immediately followed by either a 2 or a 3.
- In the series, the valid 9’s are: the second 9 (followed by 3), the third 9 (followed by 3), and the fifth 9 (followed by 2).
- Thus, there are a total of three 9’s that satisfy the conditions.
- Therefore, the answer is three.
Q15: Find the number of triangles in the given figure.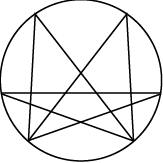 (a) 24
(a) 24
(b) 26
(c) 25
(d) More than 26
 View Answer
View Answer 
Ans: (d)
Triangles formed are: B, D, H, I, J, K, L, AB, BC, DE, EI, IJ, GH, GL, KL, BFJ, BFK, CGL, AEI, FGHJ, DEFK, DEFGH, BFJCG, AEFKB, ABEFIJ, CBFGKL, DEFGLK, .....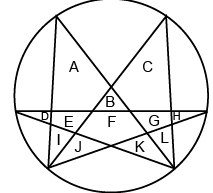 So, number of triangles formed is more than 26.
So, number of triangles formed is more than 26.
Mathematical Reasoning
Q16: Simplify: (a) 14
(a) 14
(b) 30√2
(c) 28√2
(d) 48
 View Answer
View Answer 
Ans: (c)
We have,
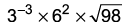
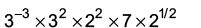
Q17: The dimensions of a cuboidal container are 12 cm x 10 cm x 8 cm. How many bottles of syrup can be poured into the container if each bottle contains 20 cm3 of syrup?
(a) 46
(b) 54
(c) 48
(d) 58
 View Answer
View Answer 
Ans: (c)
Q18: Which of the following statements is false?
(a) Every integer is a rational number.
(b) Every natural number is an integer.
(c) Every natural number is a real number.
(d) Every real number is a rational number.
 View Answer
View Answer 
Ans: (d)
- The statement "Every real number is a rational number" is incorrect because real numbers include both rational numbers (like fractions) and irrational numbers (like the square root of 2 or pi).
- On the other hand, integers are indeed rational numbers, as they can be expressed as a fraction (e.g., 5 can be written as 5/1).
- Natural numbers are a subset of integers, and they are also real numbers.
- Thus, the only false statement among the options is (d).
Q19: By selling a bicycle for ₹ 38,000, an individual incurs a loss of 20%. What price should he set to achieve a profit of 15%?
(a) ₹ 68,120
(b) ₹ 54,625
(c) ₹ 47,500
(d) ₹ 55,625
 View Answer
View Answer 
Ans: (b)
- To find the cost price (CP) of the bike, we can use the loss percentage. If selling price (SP) is ₹ 38,000 and the loss is 20%, then:
- CP = SP / (1 - Loss%) = 38,000 / (1 - 0.20) = 38,000 / 0.80 = ₹ 47,500.
- Now, to find the selling price for a 15% gain, we calculate:
- SP = CP × (1 + Gain%) = 47,500 × (1 + 0.15) = 47,500 × 1.15 = ₹ 54,625.
Q20: For which values of a and b is the polynomial x4 + ax3 + 2x2 - 3x + b divisible by x2 - 1?
(a) a = 3, b = 4
(b) a = 2, b = 4
(c) a = 3, b = -3
(d) a = 1, b = -3
 View Answer
View Answer 
Ans: (c)
- To determine the values of a and b, we need to ensure that the polynomial is divisible by x2 - 1. This means that both x = 1 and x = -1 should be roots of the polynomial.
- Substituting x = 1 into the polynomial gives us the equation: 1 + a + 2 - 3 + b = 0, simplifying to a + b = 0.
- Substituting x = -1 gives us: 1 - a + 2 + 3 + b = 0, simplifying to -a + b + 6 = 0.
- Solving these two equations, we find that a = 3 and b = -3 satisfy both conditions, confirming that option (c) is correct.
Q21: In the figure below ABCDE is a pentagon with BE || CD and BC || DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm, then find the values of x and y respectively: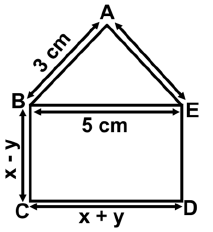 (a) 0, 5
(a) 0, 5
(b) 5, 0
(c) 3, 2
(d) 2, 5
 View Answer
View Answer 
Ans: (b)
Q22: Look at the image given below. If AOB is a straight line, then the value of x is: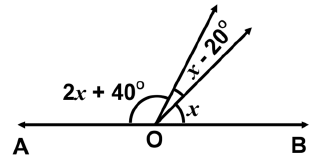 (a) 60°
(a) 60°
(b) 30°
(c) 90°
(d) 40°
 View Answer
View Answer 
Ans: (d)
Q23: Determine the highest value of n for which the number 1578n is divisible by 3.
(a) 3
(b) 9
(c) 6
(d) 8
 View Answer
View Answer 
Ans: (b)
- To check if a number is divisible by 3, we need to look at the sum of its digits.
- The digits of 1578n are 1, 5, 7, 8, and n. The sum of the known digits is 1 + 5 + 7 + 8 = 21.
- Now, we add n to this sum: 21 + n. For this to be divisible by 3, 21 + n must also be divisible by 3.
- Since 21 is already divisible by 3, n must also be a multiple of 3. The possible values for n from the options are 3, 6, 9.
- The greatest value among these options is 9, making it the correct answer.
Q24: The average of a group of 7 numbers is 81. If one number 'X' is taken out, the average of the rest becomes 78. What is the value of X?
(a) 21
(b) 48
(c) 84
(d) 99
 View Answer
View Answer 
Ans: (d)
- To find the total of the 7 numbers, multiply the mean by the number of items: 81 * 7 = 567.
- After removing 'X', the total of the remaining 6 numbers is 78 * 6 = 468.
- Now, to find 'X', subtract the total of the remaining numbers from the original total: 567 - 468 = 99.
- Thus, the value of 'X' is 99.
Q25: Determine the coordinates on the graph of the equation 2x + 5y = 18 where the x-coordinate is half of the y-coordinate.
(a) (4, 2)
(b) (3/2, 3)
(c) (5, 5/2)
(d) (7/2, 7)
 View Answer
View Answer 
Ans: (b)
- To find the point, we start with the equation 2x + 5y = 18.
- We know that the abscissa (x) is 1/2 of the ordinate (y), so we can express this as x = (1/2)y.
- Substituting x in the equation gives us 2(1/2)y + 5y = 18, simplifying to y + 5y = 18, or 6y = 18.
- Solving for y gives y = 3, and substituting back gives x = (1/2)(3) = 3/2.
- Thus, the point is (3/2, 3), which matches option (b).
Q26: If ∠A and ∠B are complementary angles and ∠A is x, which equation can be used to determine ∠B, represented by y?
(a) y = (90° + x)
(b) y = (90° - x)
(c) y = (180° – x)
(d) y = (x + 180°)
 View Answer
View Answer 
Ans: (b)
- Complementary angles are two angles that add up to 90°.
- Given that ∠A is x, we can express ∠B as 90° - x.
- This means that to find ∠B, we subtract the measure of ∠A from 90°.
- Thus, the correct equation to find ∠B is y = (90° - x).
Q27: In the given figure, OB = BA = 14 cm and semicircles are drawn on OB, BA and OA as diameters. Then, the perimeter of the shaded area is: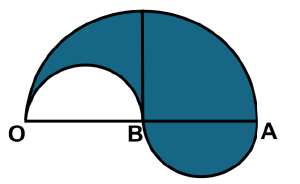 (a) 80 cm
(a) 80 cm
(b) 176 cm
(c) 264 cm
(d) 352 cm
 View Answer
View Answer 
Ans: (a)
Q28: If a solid sphere with a radius of r is melted and reshaped into a solid cone with a height of r, what is the radius of the base of the cone?
(a) 3r
(b) r
(c) 4r
(d) 2r
 View Answer
View Answer 
Ans: (d)
- The volume of a sphere is given by the formula (4/3)πr³.
- The volume of a cone is calculated using the formula (1/3)πr²h.
- When the sphere is melted, its volume remains the same, so we set the volume of the sphere equal to the volume of the cone.
- By substituting the height of the cone (r) into the cone's volume formula and solving for the radius of the cone's base, we find that the radius is 2r.
Q29: How many measurements are required to uniquely define a quadrilateral?
(a) 4
(b) 3
(c) 5
(d) 6
 View Answer
View Answer 
Ans: (c)
- To uniquely construct a quadrilateral, you need 5 measurements. This can include the lengths of the sides and the angles.
- With 4 measurements, you might not have enough information to determine the shape and size of the quadrilateral.
- 3 measurements are insufficient as they do not provide enough data to define all four sides and angles.
- Thus, the correct answer is 5 measurements to ensure a unique construction of a quadrilateral.
Q30: The perimeter of an isosceles triangle is 32 cm. The ratio of one of the equal sides to its base is 3:2. Find the area of the triangle
(a) 48 cm2
(b) 28√3 cm2
(c) 32√2 cm2
(d) 44 cm2
 View Answer
View Answer 
Ans: (c)
- Let the length of the equal sides be 3x and the base be 2x. The perimeter is given by the equation: 3x + 3x + 2x = 32.
- Simplifying this gives 8x = 32, leading to x = 4. Thus, the equal sides are 12 cm and the base is 8 cm.
- To find the area, we can use the formula: Area = 1/2 * base * height. First, we need to find the height using the Pythagorean theorem.
- The height can be calculated as √(122 - 42) = √(144 - 16) = √128 = 8√2. Therefore, the area is 1/2 * 8 * 8√2 = 32√2 cm2.
Q31: Two coins are tossed at the same time 500 times, resulting in the following outcomes: No head, One head, Two heads. What is the probability of getting at least one head?
(a) 98/125
(b) 198/125
(c) 198/500
(d) 392/195
 View Answer
View Answer 
Ans: (a)
- To find the probability of getting at least one head, we first need to determine the total outcomes from the 500 tosses.
- From the results, if we denote the number of times we got no heads as X, then the probability of getting at least one head is calculated as 1 - P(no heads).
- Assuming the number of times no heads appeared is 100, then the probability of no heads is 100/500 = 1/5.
- Thus, the probability of getting at least one head is 1 - 1/5 = 4/5, which simplifies to 98/125.
Q32: The area of a rectangle with length x2 + 2xy + y2 and breadth x2 - 2xy + y2 is _______.
(a) x4 + y4 - 2x2y2
(b) x2 + y2 - 3x2y2
(c) x4 + y4 + 2x2y2
(d) x4 - y4 + 2x2y2
 View Answer
View Answer 
Ans: (a)
- To find the area of a rectangle, we multiply its length and breadth.
- The length is given as x2 + 2xy + y2, and the breadth is x2 - 2xy + y2.
- When we multiply these two expressions, we can use the difference of squares formula, which helps simplify the calculation.
- After performing the multiplication, we arrive at the result: x4 + y4 - 2x2y2.
Q33: If the angles A, B, C, and D of a quadrilateral ABCD are in the ratio 11:19:21:9, then which of the following is correct?
(a) ABCD is a square
(b) ABCD is a trapezium with AD || BC
(c) ABCD is a rectangle
(d) ABCD is a rhombus
 View Answer
View Answer 
Ans: (b)
- The angles of a quadrilateral always add up to 360 degrees.
- Given the ratio 11:19:21:9, we can find the actual angles by calculating their total parts: 11 + 19 + 21 + 9 = 60 parts.
- Each part equals 360/60 = 6 degrees, so the angles are 66, 114, 126, and 54 degrees respectively.
- Since one pair of angles (A and D) are not equal, but the other pair (B and C) are not equal either, this indicates that ABCD is a trapezium with AD parallel to BC.
Q34: While attempting a Mathematics problem, Karan squared a certain number and then took away 25 from it instead of performing the required operation, which was to first subtract 25 from the number and then square it. Surprisingly, he arrived at the correct answer. What was the original number?
(a) 48
(b) 13
(c) 11
(d) 19
 View Answer
View Answer 
Ans: (b)
- The problem states that Karan squared a number and then subtracted 25, but he should have subtracted 25 first and then squared the result.
- Let’s denote the original number as x. According to Karan's method, he calculated x² - 25.
- The correct method would be (x - 25)². For Karan to get the same result, we set the two expressions equal: x² - 25 = (x - 25)².
- Solving this equation leads us to find that x = 13, which is the original number he worked with.
Q35: Mr. Sharma invested ₹ 20,000 at an interest rate of 20% per annum. The interest was compounded half-yearly for the first one year and in the next year, it was compounded yearly. What will be the interest earned at the end of 2 years?
(a) ₹ 9,040
(b) ₹ 8,600
(c) ₹ 9,800
(d) ₹ 8,040
 View Answer
View Answer 
Ans: (a)
- To calculate the interest earned, we first find the amount after the first year with half-yearly compounding.
- For the first 6 months, the interest is calculated on ₹ 20,000 at 10% (half of 20%), which gives ₹ 2,000.
- After 6 months, the new principal becomes ₹ 22,000. For the next 6 months, the interest is again 10% on ₹ 22,000, resulting in ₹ 2,200.
- At the end of the first year, the total amount is ₹ 24,200. In the second year, the interest is compounded yearly on this amount at 20%, giving ₹ 4,840.
- Thus, the total interest earned over 2 years is ₹ 9,040.
Everyday Mathematics
Q36: The average weight of 4 men increases by 3 kg when one of them, who weighs 120 kg, is substituted with another man. What is the weight of the new man?
(a) 140 kg
(b) 150 kg
(c) 132 kg
(d) 160 kg
 View Answer
View Answer 
Ans: (c)
- The average weight of the 4 men increases by 3 kg. This means the total weight of the 4 men increases by 4 x 3 = 12 kg.
- Initially, the total weight of the 4 men was 4 times the average. After replacing the 120 kg man, the new total weight becomes original total + 12 kg.
- If we denote the weight of the new man as x, we can set up the equation: (total weight - 120 + x) = total weight + 12.
- Solving this gives us x = 132 kg, which is the weight of the new man.
Q37: A vegetable vendor purchases 240 kg of onions for ₹ 380. If 20% of the onions are not usable, what should be the average selling price per kilogram of the remaining onions to achieve a profit of 25%?
(a) ₹ 2.47
(b) ₹ 3.50
(c) ₹ 2.10
(d) ₹ 1.47
 View Answer
View Answer 
Ans: (a)
- First, calculate the total usable onions: 20% of 240 kg is 48 kg, so usable onions = 240 kg - 48 kg = 192 kg.
- Next, determine the cost price of the usable onions: The total cost is ₹ 380, so the cost price per kg = ₹ 380 / 240 kg = ₹ 1.58.
- To achieve a 25% profit, the selling price per kg must be: Cost price per kg + 25% of cost price = ₹ 1.58 + (25/100 * ₹ 1.58) = ₹ 1.58 + ₹ 0.395 = ₹ 1.975.
- Finally, to find the average selling price for the 192 kg to make a profit of 25%, the total selling price needed is: Total cost + Profit = ₹ 380 + (25% of ₹ 380) = ₹ 380 + ₹ 95 = ₹ 475. Therefore, average price per kg = ₹ 475 / 192 kg = ₹ 2.47.
Q38: A solid cylinder of lead 8 m high and 2 m radius is melted and recast into a cone of radius 1.5 m. What is the height of the cone?
(a) 16.67 m
(b) 21.35 m
(c) 42.67 m
(d) 31.35 m
 View Answer
View Answer 
Ans: (c)
- To find the height of the cone, we first calculate the volume of the original cylinder using the formula: Volume = πr²h, where r is the radius and h is the height.
- The volume of the cylinder is: Volume = π(2 m)²(8 m) = 32π m³.
- Next, we use the volume of the cone formula: Volume = (1/3)πr²h, where r is the radius of the cone and h is its height.
- Setting the volumes equal (since the lead is recast), we have: 32π = (1/3)π(1.5 m)²h. Simplifying gives h = 42.67 m.
Q39: A rectangular field has an area of (14x² - 11x - 15) m². What could be the possible expression for length and breadth of the field
(a) (3x - 2) m and (5x + 8) m
(b) (7x + 5) m and (2x - 3) m
(c) (4x + 2) m and (3x - 7) m
(d) (6x - 5) m and (2x - 3) m
 View Answer
View Answer 
Ans: (b)
- The area of the rectangle is given as (14x² - 11x - 15) m².
- To find the length and breadth, we need to factor this expression.
- Factoring gives us (7x + 5) and (2x - 3), which matches option (b).
- Thus, the possible expressions for the dimensions of the field are (7x + 5) m and (2x - 3) m.
Q40: 8 men can complete a task in 20 days, while 8 women can finish it in 32 days. How many days will it take for 5 men and 8 women to finish the same task together?
(a) 10 days
(b) 12 days
(c) 16 days
(d) 18 days
 View Answer
View Answer 
Ans: (c)
- First, calculate the work done by 1 man in a day: 8 men complete the work in 20 days, so 1 man does 1/160 of the work per day.
- Next, find the work done by 1 woman: 8 women finish the work in 32 days, meaning 1 woman does 1/256 of the work per day.
- Now, calculate the combined work of 5 men and 8 women: 5 men do 5/160 = 1/32 of the work, and 8 women do 8/256 = 1/32 of the work.
- Adding these, 5 men and 8 women together complete 1/32 + 1/32 = 1/16 of the work in one day.
- Thus, they will finish the work in 16 days (since 1 divided by 1/16 equals 16).
Q41: The difference between the current ages of two individuals is 10 years. Fifteen years ago, the older individual was twice the age of the younger one. What is the current age of the older individual?
(a) 55 years
(b) 45 years
(c) 35 years
(d) 25 years
 View Answer
View Answer 
Ans: (c)
- Let the current age of the younger person be Y years. Then, the age of the older person is Y + 10 years.
- Fifteen years ago, the younger person's age was Y - 15, and the older person's age was (Y + 10) - 15 = Y - 5.
- According to the problem, fifteen years ago, the older person was twice the age of the younger person: Y - 5 = 2(Y - 15).
- Simplifying this gives Y - 5 = 2Y - 30, leading to Y = 25. Therefore, the older person's age is 25 + 10 = 35 years.
Q42: In an examination, a minimum of 55% of the total marks is needed to pass. A student scores 520 marks but fails by 5% marks. What is the total maximum aggregate marks?
(a) 960
(b) 1050
(c) 1205
(d) 1040
 View Answer
View Answer 
Ans: (d)
- The student needs to achieve 55% to pass.
- Since the student failed by 5%, they actually needed 60% to pass.
- Let the maximum aggregate marks be x. Then, 60% of x = 520.
- From this, we can calculate x = 520 / 0.60 = 1040.
- Thus, the maximum aggregate marks are 1040.
Q43: The probability of selecting a girl from a class is 3/8, and there are 360 students in the class. Find the number of boys in the class
(a) 225
(b) 135
(c) 215
(d) 240
 View Answer
View Answer 
Ans: (a)
- To find the number of boys, first calculate the number of girls in the class. The probability of selecting a girl is 3/8, which means that out of every 8 students, 3 are girls.
- Using the total number of students (360), the number of girls can be calculated as: (3/8) * 360 = 135.
- Now, to find the number of boys, subtract the number of girls from the total number of students: 360 - 135 = 225.
- Thus, the number of boys in the class is 225.
Q44: Duke is learning about the famous mathematician Euclid. According to Euclid's definition, the ends of a line are:
(a) Breadthless
(b) Points
(c) Lengthless
(d) Segments
 View Answer
View Answer 
Ans: (b)
Q45: In a town, 35.4% of the people are not literate, 27% have education up to primary school, and 18.6% have education up to middle school. The people with education up to high school are twice the number of people with education up to pre-university. Of the remaining, 660 are graduates. If the population of the town is 15,000, then what is the number of people with education up to high school?
(a) 3120
(b) 1560
(c) 1460
(d) None of these
 View Answer
View Answer 
Ans: (c)
Achievers Section
Q46: A man had certain number of cookies with him. At first, he wanted to divide it amongst his three children. When the division was done, one cookie remained. Just then, one of the cousins came. Now it was possible to divide the same number of cookies equally between the four children. What is the minimum number of cookies with the man?
(a) 13
(b) 17
(c) 16
(d) 15
 View Answer
View Answer 
Ans: (c)
Q47: The line joining the centre of a circle to the midpoint of a chord (except diameters) is always:
(a) Parallel to the chord
(b) Perpendicular to the chord
(c) Equal to the chord
(d) Tangent to the chord
 View Answer
View Answer 
Ans: (b)
Q48: What least number must be subtracted from 1294 so that the remainder when divided by 9, 11, 13 will leave in each case the same remainder 6?
(a) 0
(b) 1
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (b)
Q49: If the roots of the quadratic equation x2 - 3x - 304 = 0 are α and β, then the quadratic equation with roots 3α and 3β is:
(a) x2 - 9x - 2736 = 0
(b) x2 + 9x - 2736 = 0
(c) x2 - 9x + 2736 = 0
(d) x2 + 9x + 2736 = 0
 View Answer
View Answer 
Ans: (a)
Q50: In the adjoining figure, if the radius of each of the four outer circles is r, then what is the radius of the inner circle?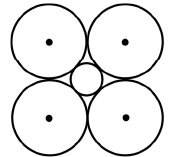 (a) 2r/(√2 + 1)
(a) 2r/(√2 + 1)
(b) r/√2
(c) (√2 - 1) r
(d) √2 r
 View Answer
View Answer 
Ans: (c)
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Model Test Paper -3 - Mathematics Olympiad for Class 9
| 1. What topics are covered in the Maths Olympiad Model Test Paper for Class 9? |  |
| 2. How can I prepare effectively for the Maths Olympiad? |  |
| 3. Are there any specific strategies for solving Logical Reasoning questions in the Olympiad? |  |
| 4. What is the importance of Everyday Mathematics in the Maths Olympiad? |  |
| 5. How is the Achievers Section different from other sections in the Maths Olympiad? |  |















