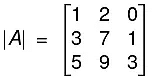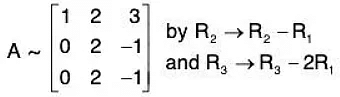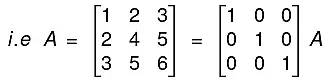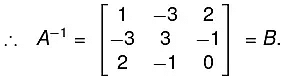Matrices & Determinants: Matrix Algebra - 2 | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
In part 1 of Matrices and Determinants, we have covered the topics: Introduction to matrices, Types of matrices, Transpose of a matrix, and Equal Matrices. In this part, we will start with the minor of a matrix and the rank of a matrix.
What is Minor of a Matrix?
Minor of the matrix for a particular element in the matrix is defined as the matrix obtained after deleting the row and column of the matrix in which that particular element lies. Here the minor of the element aij is denoted as Mij. For example, for the given matrix A, the minor of a12 is the part of the matrix after excluding the first row and the second column of the matrix.

The minor of the element a12 is as follows. 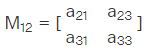
Similarly, we can take the minors of the matrix and form a minor matrix M of the given matrix A as: 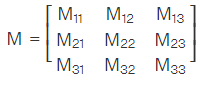
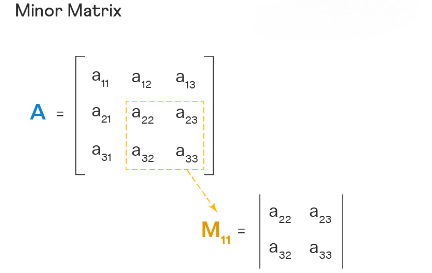
How to Find Minor of Matrix?
There are three simple steps to find the minor of the matrix.
- First identify and exclude the row and the column which contains the particular element within the matrix.
- As a second step, form a new smaller matrix with the remaining elements, to represent the minor of the particular element of the matrix.
- Finally, find the determinant of the minor of each element of the matrix, and form a new matrix containing the minor values of the respective elements.
This creates the minor of matrix.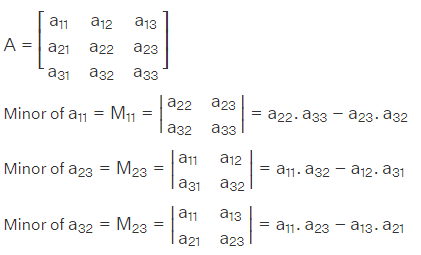
Similarly we can find the minor of each element of the matrix A. Further, we can form the minor of matrix A by writing the minor of each element in the matrix array.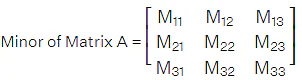
Cofactors: The minor Mij multiplied by (-1)i+j is called the cofactor of the element aij. Cofactor of aij =Aij = (-1)i+j Aij.
Rank of a Matrix
A number r is said to be the rank of a matrix A if it possesses the following two properties:
- There is at least one minor of A of order r which does not vanish.
- Every minor of A of order (r + 1) or high vanish. All minors of order greater than r will vanish if all minors of order (r + 1) are zero.
Rank of a matrix is the order of the highest non-vanishing minor of the matrix.
From the above definition we have the following two useful results.
- The rank of matrix A is ≥ r, if there is at least one minor of A of order r which does not vanish.
- The rank of matrix A is ≤ r if all the minors of A of order (r + 1) or higher vanish.
Some important points:
- The rank of a matrix whose minors of order n are all zero is < n.
- We assign the rank n to the matrix which has at least one non-zero minor of order n; n being the order of any highest minor of the matrix, e.g. the rank of every onward non-singular matrix is n.
- Again rank of every non-zero matrix is ≥ 1, we assign the rank zero to every zero matrix.
We shall denote the rank of matrix A by the symbol ρ(A).
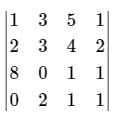
Example. Find the rank of the matrix 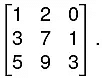
= 1(21 - 9) - 2 (9 - 5) + 0 (27 - 35)
= 12 - 8 = 4 ≠ 0.
ρ(A) = 3
Rank of a Matrix (by elementary transformations of a matrix)
Consider a matrix A = (aij)m x n then its rank can be easily calculated by applying elementary transformations given below:
- Interchange any two rows (i.e. Rij) or columns (Cij).
- Multiplication of the elements of a row (or a column) say Ri(or Ci) by a non-zero number k is denoted by k Ri(or kCi).
- The addition to the elements of ith row (or column) the corresponding elements of any other row say jth row (or column) multiplied by a non-zero number k is denoted by Rij(k) or Cij(k). Any elementary operation is called a row transformation (or a column transformation) according to what it operates on a row (or column).
- In the easy form we use the following notations:
- Ri ↔ Rj (interchange of ith and jth row) (Ci ↔ Cj (interchange of ith and jth column)
- Ri ↔ k Ri(Ci → k Ci) means multiply ith row (or column) by k ≠ 0.
- R.↔ Ri + kRj (Ci → Ci + kC) means to multiply each element of jth row (or column) by non zero number k and add it to the corresponding elements of ith row (column).
Note - Rank of a matrix does not alter by applying elementary row transformation (or column transformations).
Rank of a Matrix A = (aij), m*n by Reducing it to Normal Form.
Every non-zero matrix [say A = (aij)m*n] of rank r, by a sequence of elementary row (or column) transformations be reduced to the forms: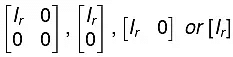
where lr is a r*r unit matrix of order r and 0, denotes null matrix of any order. These forms are called as normal forms or canonical forms of the matrix A. The order of the unit matrix lr is called the rank of the matrix A.
The rank of a matrix does not alter by pre-multiplication or post-multiplication with a non singular matrix.
Echelon Form of a Matrix
A matrix A = (aij)m*n is said to be in Echelon form, if
- All the non-zero rows, if any, precede the zero rows.
- The number of zeros preceding the first non-zero element in a row is less than the number of such zeros in the succeeding (or next) row.
- The first non-zero element in every row is unity.
Example: The matrix is in echelon form.Since in A,
is in echelon form.Since in A,
(i) The zero rows precede the zero row.
(ii) The number of zeros preceding the first non-zero element in rows R2, R3, R4 are 1, 2 and 5 which are in ascending order.
(iii) The first non-zero element in each row is 1.
NOTE: When a matrix is converted in Echelon form, then the number of non zero rows of the matrix is the rank of the matrix A.
Example. Determine the rank of the matrix, by E-transformations.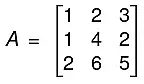
Now,
Now applying the elementary transformations.
R3→ R3 - R2, we have
orHere third order minor viz
(vanishes) while the second order minor
so the rank of the matrix is 2.
Elementary matrix
A matrix obtained by the application of any one of the elementary row (or column) operation to the identity matrix is called an elementary row (or column) matrix.
The following notations are used for the elementary row matrices.
(i) Eij Elementary row matrix obtained by the operation Rij.
(ii) Ei(k) Elementary row matrix obtained by the operation kRi.
(iii) Eij(k) Elementary row matrix obtained by the operation Ri + kRj.
(iv) E’ij(k) transpose of elementary matrix Eij(k), which can also be obtained by the operation Cij(k).
Inverse of a Matrix
Definition
Let A be a square matrix. If there exists a matrix B, such that AB = I = BA, where I is a unit matrix, then B is called the inverse of A and is denoted by A-1 and matrix A is a non-singular matrix. Non Singular matrix is a square matrix whose determinant is a non-zero value. If a matrix has an inverse, the matrix is said to be invertible
Note: The matrix B = A-1 will also be a square matrix of the same order as A.
Theorems on Inverse of a matrix
Theorem.
Every invertible matrix possesses a unique inverse.Theorem. The inverse of the product of matrices of the same type is the product of the inverses of the matrices in reverse order i.e.
(AB)-1 = B-1 A-1, (ABC)-1 = C-1 B-1 A-1 and (A-1 B-1)-1 = BA.
Theorem. The operations of a transpose and inverting are commutative, i.e. (A’)-1 = (A-1)’ where A is a m x n non-singular matrix, i.e. det A≠ 0.
Theorem. If a sequence of elementary operations can reduce a non-singular matrix A of order n to an identity matrix, then the sequence of the same elementary operations will reduce the identity matrix ln to inverse of A.
i.e. If (Er.Er_1, E2 . E1)A = ln
then (Er.Er_1 .. E2.E1) ln = A-1.
This is also known as Gauss-Jorden reduction method for finding inverse of a matrix.
Theorem. The inverse of the conjugate transpose of a matrix A (order m * n) is equal to the conjugate transpose of the matrix inverse to A, i.e. ( Aθ)-1 = (A-1)θ.
Method of finding inverse of a non-singular matrix by elementary transformations.
The method is that we take A and I (same order) and apply the row operations on both successively elementary transformations till A become I. When A reduces to I, I reduces to A-1.Example. Find the inverse of the matrix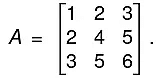
Write A = IA
By R2 - 2R1, R3 - 3R1
By R2 + R3
By R, + 3R3, R2 - 3R3
By R2 + 2R2
By - R2, - R3
⇒ I = BA
Inverse of a Matrix (another form)
The inverse of A is given by 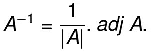 The necessary and sufficient condition for the existence of the inverse of a square matrix A is that IAI ≠ 0, i.e. matrix should be non-singular.
The necessary and sufficient condition for the existence of the inverse of a square matrix A is that IAI ≠ 0, i.e. matrix should be non-singular.Properties of Inverse matrix:
If A and B are invertible matrices of the same order, then
- ( A-1)-1 = A.
- (AT)-1 = (A-1)T
- (AB)-1 = B-1A-1
- (Ak)-1 = (A-1)k , k ∈ ℕ
- adj(A-1) = (adj A)-1
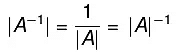
- A = diag (a1,a2....an) ⇒ A-1 = diag (a1-1a2-2..., an-1)
- A is a symmetric matrix ⇒ A-1 is also a symmetric matrix.
- A is a diagonal matrix, IAI ≠ 0 ⇒ A-1 is also a triangular matrix.
- A is a scalar matrix ⇒ A-1 is also a scalar matrix.
- A is a triangular matrix, IAI ≠ 0 ⇒ A-1 is also a triangular matrix.
- Every invertible matrix possesses a unique inverse.
- Cancellation law with respect to multiplication.
- If A is a non-singular matrix i.e., if IAI ≠ 0, then A-1 exists and
AB = AC ⇒ A-1 (AB) = A-1(AC)
⇒ (A-1A)B = (A-1A)C
⇒ IB = IC ⇒ B = C
∴ AB = AC ⇒ B = C = ⇔ IAI ≠ 0.
Determinants
Consider the following simultaneous equations
a11x + a12y = k1,
a21x + a22y = k2
- These equations have the solution
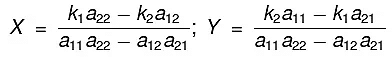 provided the expansion a11a22 - a12a21 ≠ 0. T
provided the expansion a11a22 - a12a21 ≠ 0. T - This expression a11a22 - a12a21 is represented by
 and is called a determinant of second order.
and is called a determinant of second order. - The number a11,a12,a21,a22 are called elements of the determinant.
- The value of the determinant is equal to the product of the elements along the principal diagonal minus the product of the off-diagonal elements.
- Similarly a symbol
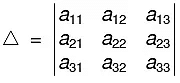 is called a determinant of order 3 and its value is given by
is called a determinant of order 3 and its value is given by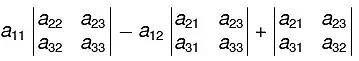 = a11 (a22a33 - a32a23) - a12(a21a33 - a31a23 ) + a13(a21a32 - a31a22) ...(1)
= a11 (a22a33 - a32a23) - a12(a21a33 - a31a23 ) + a13(a21a32 - a31a22) ...(1)
Rule
a11 (determinant obtained by removing the row and column intersecting at a11). - a12 (determinant obtained by removing the row and column intersecting at a12) + a13 (determinant obtained by removing the row and column intersecting at a13).
This is called expansion of the determinant along the first row.
Note: In a determinant of order 3 there are 3 rows and 3 columns and its value can be found by expanding it along any of its rows of along any of its columns. In these expansions the element a., is multiplied by (-1)i+j to fix the sign of aij.
Properties of Determinants
- The value of the determinant does not change by changing rows into columns and columns into rows
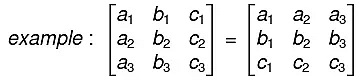
- If any two adjacent rows (or columns) of a determinant are interchanged, the value of the determinant is multiplied by -1.

Note: In case any row (or column) of a determinant A be passed over n rows (or columns) then the resulting determinant is (-1)n Δ. (the fourth row has passed over three parallel rows) - If any two rows or two columns of a determinant are identical then the determinant vanishes.
- If all the elements of any row (or any column) of a determinant are multiplied by the same factor k then the value of the new determinant is k times the value of the given determinant.
- If in a determinant each element in any row (or column) consists of the sum of r terms, the determinant can be expressed as the sum of r determinants of the same order.
- If to the elements of a row (or column) of a determinant are added m times the corresponding elements of another row (or column), the value of the determinant so obtained is equal to the value of the original determinant.
- When at least one row (or column) of a matrix is a linear combination of the other rows (or columns) the determinant is zero.
- The determinant of an upper triangular or lower triangular matrix is the product of the main diagonal entries.
- The determinant of the product of two square matrices is the product of the individual determinants:
|A.B| = IA|.|B|
One immediate application is to matrix powers:
IAI2 = IAI.IAI
and more generally IAnl = IAIn for integer n. - The determinant of the transpose of a matrix is the same as that of the original matrix:
IATI = IAI.
General rule. One should always try to bring in as many zeros as possible in any row (column) and then expand the determinant with respect to that row (column)
Thus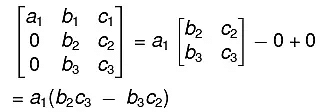 ➤ Minors and cofactors
➤ Minors and cofactors
Reciprocal Determinant
If in a given determinant each element is replaced by its cofactor, then the determinant so formed is called reciprocal or inverse determinant of the given determinant. If the original determinants is A then its reciprocal determinant is denoted by Δ’.
If A is a determinant of order n and A’ be its reciprocal determinant then Δ’ = Δn-1.
|
558 videos|198 docs
|
FAQs on Matrices & Determinants: Matrix Algebra - 2 - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the inverse of a matrix? |  |
| 2. How do you find the inverse of a matrix? |  |
| 3. What is the determinant of a matrix? |  |
| 4. How can you determine if a matrix has an inverse? |  |
| 5. Can a matrix have more than one inverse? |  |