Maxwell - Boltzmann Statistics: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. Calculate the fraction of the oxygen molecule with velocities between 199m/ sec and 201m/ sec at temperature 27oC .
v =
= 200m/sec and dv = 201-199 = 2m/sec
m = 32 x 1.67 x10-27 kg k = 1.38 x 10-23 J / K T = 27 + 273 = 300k
f (v ) = 2.29 x 10-3
Q.2. For two dimension For maxwell’s distribution for velocities v of molecules at equilibrium temperature T .
(a) Find average value of v at equilibrium temperature.
(b) Find average value of v2 at equilibrium temperature.
(c) Find average value of 1/v at equilibrium temperature.
f (v ) =
(a)
(b)
(c)
Q.3. A system of four identical distinguishable particles has energy3ε . The single particle states are available at energies 0,ε , 2ε , and 3ε (a) Make a table to show all possible distributions of the particles in the quantum states giving the number of particles in each quantum state. (b) Write the probability of each distribution. (c) Find the average number n(E) of particles in each energy E . (d) Sketch n(E) versus E .
(a) The possible distribution which can give a total energy 3e are shown in the table below.
(b) The total number of ways to get energy 3e is therefore 4 +12 + 4 = 20 . The probabilities of the three configurations are therefore 4 / 20 /,12 / 20 /, 4 / 20 . (c) The quantum state with zero energy can have 3 particles with probabilities 4 / 20, 2 with probability 12 / 20 and one with probability 4 / 20 . The average number of particles with zero energy is, therefore,
= 2.0
Similarly,
= 1.2
= 0.6
= 0.2
(d) The sketch of n (E ) versus E is shown in figure 23.W1 . Though it is an example only to illustrate the methods of statistical mechanics, with just four particles, the general trends of n (E ) versus E reflected. The lower energy levels are more densely populated than the higher energy levels.
Q.4. A battle of volume 1 litre is filled with hydrogen gas. Find the number of quantum states available in the energy range 0.020 to 0.021.
The number of quantum states in the energy range E to E + dE is
Mass of a hydrogen molecule = 2 x 1.67 x10-27 kg . The volume is 1litre = 10-3 m3 . The energy E = 0.020 x 1.6 x 10-19J and dE = 0.001 x 1.6 x 10-19 J . Thus
g (E) dE =
= 1.4 x1026 .
Q.5. In a gas of atomic hydrogen at 273K what is the relative population of the first excited state?
The ground state of a hydrogen atom is at E =-13.6 eV and is 2 - fold degenerate. The first excited state is at E =-3.4 eV and is 8 -fold degenerate. The probability of a hydrogen atom occupying a given quantum state is proportional to e- E / kT . Thus, the probability of occupying the first excited state is
Thus,
=
This shows that there will be hardly and hydrogen atom in the excited states.
Q.6. For Maxwell’s distribution for velocities v of molecules at equilibrium temperature T . Find average value of 1/v.
f(v) =
=
=
Q.7. Clausius assumed that all molecules move with velocity v with respect to container prove that average of relative velocity i.e. velocity of one molecule with respect to another is 4/3v .
Now all the direction of velocity v are equally probable .the probability that v lying within solid angle θ and θ + dθ is f (θ) =
Q.8. Consider a gas of atoms obeying Maxwell-Boltzmann statistics. The average value of 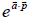 over all the moments
over all the moments 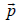 of each of the particles (where
of each of the particles (where 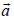 is a constant vector and a is the magnitude, m is the mass of each atom, T is temperature and k is Boltzmann’s constant) is
is a constant vector and a is the magnitude, m is the mass of each atom, T is temperature and k is Boltzmann’s constant) is
where
is Maxwell probability distribution at temperature T.
Q.9. Consider 10 atoms fixed at lattice sites. Each atom can have magnetic moment μB or -μB in the z -direction. Let f (μ) denote the probability that the magnetic moment of the system is μ. Assuming statistical mechanics to hold, find the value of f (2μB) / f(0).
The magnetic moment can be 2μB if 6 atoms are in +μB state and 4 in -μB state.
This can happen in n1 ways where,
n1 =
= 210
For magnetic moment to be zero, five atoms should be in +μB state five in -μB state. This can happen in n2 ways where,
The probabilities will be proportional to these number. Hence
Q.10. A bottle of volume 1 litre is filled with hydrogen at NTP. Find the number of molecules in the energy range 0.0235 eV to 0.0236 eV .
The number of molecules in the energy range E to E + dE is given by
There are 6 x1023 molecules in 23.4 liters at NTP . Thus the number of molecules in 1litre is
N =

Also, kT = (8.617 x 10-5 eV / K) x (273K) = 0.0235 eV
The range given is 0.0235 eV to 0.0236 eV . Writhing this as E to E + dE , E= kT , E = kT or E / ( kT ) =1 .
Also
Thus, N(E)dE =
=
|
6 videos|20 docs|32 tests
|
FAQs on Maxwell - Boltzmann Statistics: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is Maxwell-Boltzmann statistics? |  |
| 2. How are Maxwell-Boltzmann statistics applied in IIT JAM? |  |
| 3. What is the significance of Maxwell-Boltzmann statistics in IIT JAM? |  |
| 4. Can Maxwell-Boltzmann statistics be applied to all types of particles? |  |
| 5. How can one calculate the average speed of particles using Maxwell-Boltzmann statistics? |  |


 = 200m/sec and dv = 201-199 = 2m/sec
= 200m/sec and dv = 201-199 = 2m/sec




 = 2.0
= 2.0 = 1.2
= 1.2 = 0.6
= 0.6 = 0.2
= 0.2

 = 1.4 x1026 .
= 1.4 x1026 .



 =
= 




 where
where  is Maxwell probability distribution at temperature T.
is Maxwell probability distribution at temperature T.


 = 210
= 210




 =
= 



















