Maxwell Relation & Thermodynamic Potential | Kinetic Theory & Thermodynamics - Physics PDF Download
Maxwell Relations
Let, F = F(x, y) and if it is perfect differential work, then dF = Mdx + Ndy
Where, M = 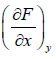 and N =
and N = 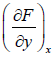 , then M and N will satisfy the condition
, then M and N will satisfy the condition 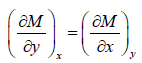
Maxwell relations are relationship between two derivatives of thermodynamic variables, and energy due to the equivalence of potential second derivative under a change of
operation order 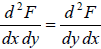 , where F is thermodynamic potential and x and y are two of its natural independent variables.
, where F is thermodynamic potential and x and y are two of its natural independent variables.
Maxwell relations are extremely important for two reasons.
First they show us that derivative of thermodynamic parameters are not all independent. This can serve as a consistency check in both experiments and in theoretical analysis.
Maxwell relations provide a method for expressing some derivative in other ways. This enables as to connect difficult measurable quantities to those which are readily accessible experimentally.
The measurement of entropy and chemical potential can not be directly measurable in lab but with the help of Maxwell relations, there thermodynamic property can be determined theoretically.
For Maxwell relation.
Let us consider Legendre the independent variable as x , and y such that
U = U (x, y), S = (x, y) V = V(x, y)
So, dU = 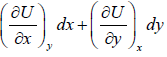
dS = 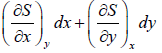
dV = 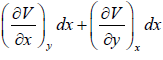
From first law of thermodynamics,
dU = TdS - PdV

Hence, U, V and S are perfect differential.
Then, 
⇒ 
 --(1)
--(1)
Similarly,
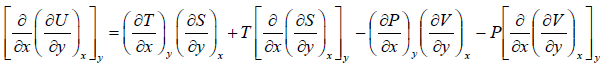 ---(2)
---(2)
Equating equation (1) and (2),
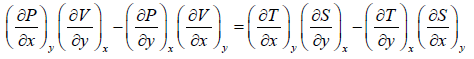 (A)
(A)
Maxwell first relation:- Put x = T, y =V
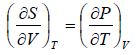
Maxwell Second Relation:- Put, x = T, y = P
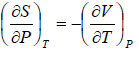
Maxwell Third Relation:- Put, x = S, y = V
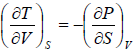
Maxwell Fourth Relation:- Put, x = S, y = P
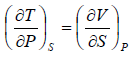
Thermodynamic potential is a scalar function used to represent the thermodynamic state of system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886.
One main thermodynamic potential that has a physical interpretation is the internal energy. It is energy of configuration of a given system of conservative forces. Expression for all other thermodynamic energy potentials are derivable via Legendre transformation.
Different Types of Thermodynamic Potential and Maxwell Relation
Thermodynamic potentials are different form of energy which can be used in different
thermodynamic process .thermodynamic potentials are path independent variables, so
they are perfect differential
If F is unique Thermodynamic potential defined by variables x and y , as F = F(x, y) and if it is perfect differential then, dF = Mdx + Ndy
where, M = 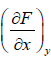 and y =
and y = 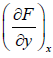 , then M and N will satisfy the condition
, then M and N will satisfy the condition 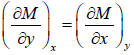
Internal Energy U
From the first laws of thermodynamics
dU = TdS - PdV
From Legendre transformation
 , from given relation one can derive Maxwell relation
, from given relation one can derive Maxwell relation
 (Maxwell’s Third Relation)
(Maxwell’s Third Relation)
Enthalpy H
The enthalpy is defined as, H = U + PV
⇒ dH = dU + PdV + VdP
From Laws of thermodynamics,
TdS = dU + PdV
dH = TdS + VdP
From Legendre transformation,
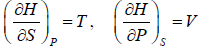
The Enthalpy H is Extensive quantity, which can not be measured directly. Thus change in enthalpy is more useful.
ΔH is positive in endothermic reaction and negative in exothermic reaction.
From above relation, one can derive Maxwell relation, 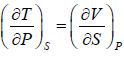 (Maxwell’s Fourth Relation).
(Maxwell’s Fourth Relation).
ΔH of a system is equal to sum of non-mechanical work done on it and the heat supplied to it.
Helmholtz Free Energy F
The Helmholtz free energy is defined as, F = U - TS
dF = dU - TdS - SdT
From laws of thermodynamics dU = TdS - PdV
dF = TdS - PdV - TdS - SdT
dF = - PdV - SdT
From Legendre transformation,
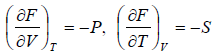
From above relation one can derive Maxwell relation, 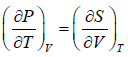 (Maxwell’s First Relation).
(Maxwell’s First Relation).
The free Energy E , which is available energy for work in reversible isothermal process.
Gibbs Energy
‘G ’ is defined as G = H - TS .
G = U + PV - TS
dG = dU + PdV - VdP - TdS - SdT
TdS - PdV + PdV + VdP - TdS - SdT
dG = VdP - SdT
From Legendre transformation,
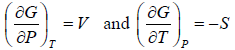
From above relation one can derive Maxwell relation,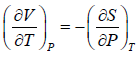 (Maxwell’s Second Relation)
(Maxwell’s Second Relation)
- Gibbs free energy is popularly known as free enthalpy.
- The Gibbs free energy is Maximum amount of non-expanding work that can be extracted from a closed system.
- The maximum work will be extracted, when the system is in reversible process.
- Gibbs free energy is also treated as chemical potential.
- In thermodynamics, chemical potential, as partial molar free energy, is a form of potential energy that can be absorbed or relived during a chemical reaction.
- The chemical potential of a species in the minute can be defined the slope of the energy at system with respect to a change in the no of moles.
μ = 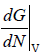 , where μ is chemical potential, G is Gibbs energy and N is no of molecules
, where μ is chemical potential, G is Gibbs energy and N is no of molecules
Example 1: Prove that internal energy U is given by
(a) U = 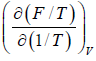
(b) H = 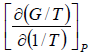
(a) F = U - TS ⇒U = F + TS
S =
U =
=
=
=
(b) H =
G = H - TS
S =
H =
=
=
|
6 videos|20 docs|32 tests
|
FAQs on Maxwell Relation & Thermodynamic Potential - Kinetic Theory & Thermodynamics - Physics
| 1. What are Maxwell relations in thermodynamics? |  |
| 2. How many types of thermodynamic potentials are there? |  |
| 3. What is the significance of Maxwell relations in thermodynamics? |  |
| 4. Can you explain the concept of thermodynamic potentials in simple terms? |  |
| 5. How are Maxwell relations used in IIT JAM exam? |  |

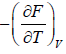
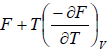 =
= 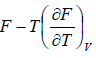 =
= 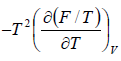 =
= 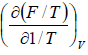
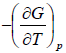
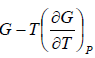 =
= 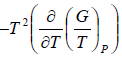 =
=