Maxwell's Equations | Electricity & Magnetism - Physics PDF Download
Maxwell’s Equation in Free Space
Electrodynamics before Maxwell’s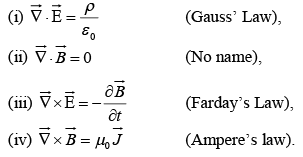
Taking divergence of equation (iii) we get
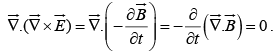 So equation (iii) is valid.
So equation (iii) is valid.
Again taking divergence of equation (iv) we have 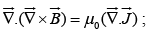
the left side must be zero, but the right side, in general, is not.
For steady currents 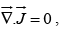 but for time varying fields
but for time varying fields  the Ampere's law can not be right.
the Ampere's law can not be right.
How Maxwell fixed Ampere’s Law
From continuity equation and Gauss Law
Thus
A changing electric field induces a magnetic field.
Maxwell called this extra term the displacement current
Integral form of Ampere's law
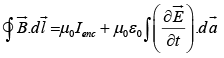
Paradox of Charging Capacitor
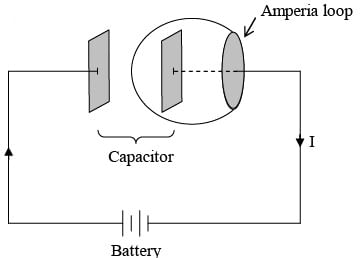
Displacement current resolves the paradox of charging capacitor. If the capacitor plates are very close together, then the electric field between them is: 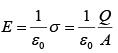 where Q is the charge on the plate and A is its area.
where Q is the charge on the plate and A is its area.
Thus, between the plates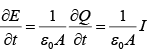
If we choose the flat surface, then E = 0 and Ienc =I
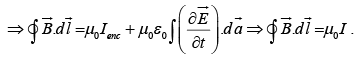
If, on the other hand, we use the balloon-shaped surface, then Ienc = 0 , then
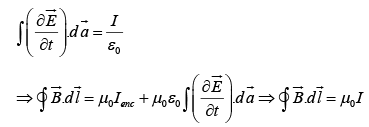
So we get the same answer for either surface, though in the first case it comes from the genuine current and in the second from the displacement current.
Maxwell’s Equation in Free Space
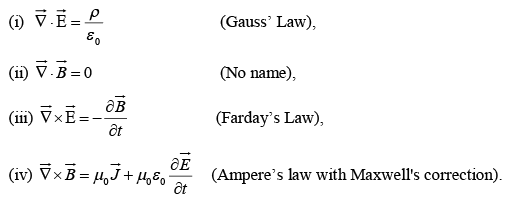
Maxwell’s Equation in Linear Isotropic Media
For materials that are subject to electric and magnetic polarization there is more convenient way to write Maxwell's equations. Inside polarized matter there will be accumulation of “bound” charge and current over which we don't have direct control. So we will reformulate Maxwell's equation in such a way as to make explicit reference only to those sources we control directly: the “free” charges and currents.
We know that an electric polarization 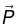 produces a bound charge density
produces a bound charge density 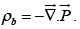
Likewise, a magnetic polarization (or “magnetization”) 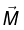 results in a bound current
results in a bound current 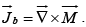
Due to time varying field any change in the electric polarization involves a flow of (bound) charge, (call it polarization current 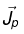 ) which must be included in the total current.
) which must be included in the total current.
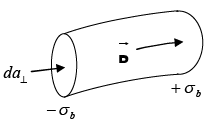
Consider a small piece of polarized material. The polarization introduces a charge density σb = P at one end and -σb at the other 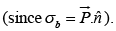 If P now increases a bit, the charge on each end increases accordingly, giving a net current-carrying,
If P now increases a bit, the charge on each end increases accordingly, giving a net current-carrying, 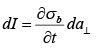
Thus the polarization current 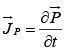
The po larizat ion current has nothing to do with the bound current, 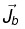 . The bound current
. The bound current 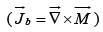 is associated with magnetization of the material and involves the spin and orbital motion of electrons.
is associated with magnetization of the material and involves the spin and orbital motion of electrons.
In view of all this, the total charge density 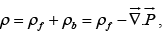
and the total current density 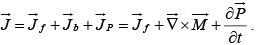
Gauss's law can now be written as:
Now, Ampere's law (with Maxwell's term) becomes
In terms of free charges and currents, then, Maxwell's equations read
(i) 
(ii) 
(iii) 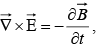
(iv) 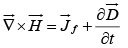
For linear media,
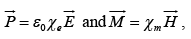
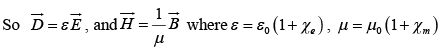
and displacement current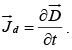
Integral form

Boundary Conditions on the Fields at Interfaces
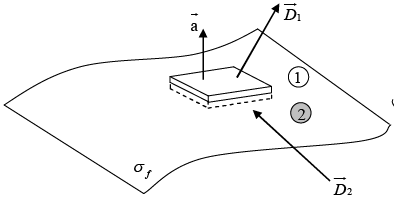
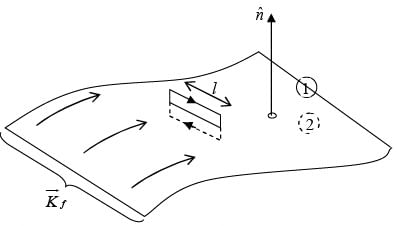
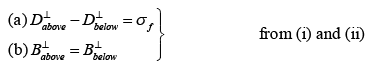
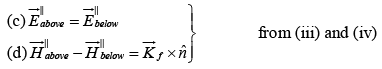
In particular, if there is no free charge or free current at the interface between medium1 and medium 2, then
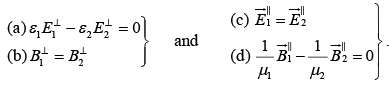
|
82 videos|32 docs|22 tests
|
FAQs on Maxwell's Equations - Electricity & Magnetism - Physics
| 1. What are Maxwell's equations and why are they important in physics? |  |
| 2. What is the physical significance of each of Maxwell's equations? |  |
| 3. How are Maxwell's equations derived? |  |
| 4. What are the implications of Maxwell's equations in the study of light? |  |
| 5. How do Maxwell's equations relate to modern technologies? |  |
















