Mean Value Theorem | Engineering Mathematics - Engineering Mathematics PDF Download
Cauchy’s Mean Value Theorem
Suppose f(x) and g(x) are 2 functions satisfying three conditions:
- f(x), g(x) are continuous in the closed interval a ≤ x ≤ b ⇒x∈[a,b]
- f(x), g(x) are differentiable in the open interval a < x < b ⇒x∈(a,b)and
- g'(x) != 0 for all x belongs to the open interval a < x < b
Then according to Cauchy’s Mean Value Theorem there exists a point c in the open interval a < c < b such that:
[f(b) - f(a)] / [g(b) - g(a)] = f'(c) / g'(c)
The conditions (1) and (2) are exactly same as the first two conditions of Lagrange's Mean Value Theorem for the functions individually. Lagrange's mean value theorem is defined for one function but this is defined for two functions.
Lagrange’s Mean Value Theorem
Suppose f : [a, b] → R
be a function satisfying these conditions:
- f(x) is continuous in the closed interval a ≤ x ≤ b
- f(x) is differentiable in the open interval a < x < b
Then according to Lagrange’s Theorem, there exists at least one point ‘c’ in the open interval (a, b) such that: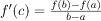
We can visualize Lagrange’s Theorem by the following figure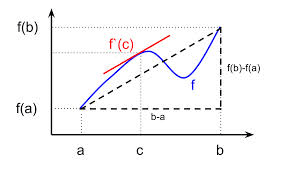 In simple words, Lagrange’s theorem says that if there is a path between two points A(a, f(a)) and B(b, f(b)) in a 2-D plain then there will be at least one point ‘c’ on the path such that the slope of the tangent at point ‘c’, i.e., (f ‘ (c)) is equal to the average slope of the path, i.e.,
In simple words, Lagrange’s theorem says that if there is a path between two points A(a, f(a)) and B(b, f(b)) in a 2-D plain then there will be at least one point ‘c’ on the path such that the slope of the tangent at point ‘c’, i.e., (f ‘ (c)) is equal to the average slope of the path, i.e.,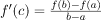
Example: Verify mean value theorem for f(x) = x2 in interval [2, 4].
Solution: First check if the function is continuous in the given closed interval, the answer is Yes. Then check for differentiability in the open interval (2, 4), Yes it is differentiable.
f'(x) = 2x
f(2) = 4
and f(4) = 16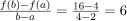
Mean value theorem states that there is a point c ∈ (2, 4) such that
f' (c) = 6
But
f' (x) = 2x
which implies c = 3. Thus at c = 3 ∈ (2, 4), we have
f' (c) = 6
Rolle’s Mean Value Theorem
Rolle's Mean Value Theorem applies to a function f(x) under certain conditions:
- Continuous: The function f(x) must be continuous within the closed interval [a, b]. This means there are no breaks, jumps, or holes in the function's graph between a and b.
- Differentiable: The function f(x) needs to be differentiable in the open interval (a, b). Differentiability implies that the function has a defined derivative (slope) at every point in this interval, meaning the graph has a tangent line at each point.
- Equal Endpoints: The values of the function at the endpoints of the interval must be equal, i.e., f(a) = f(b). This condition ensures that the function starts and ends at the same height within the interval.
Then according to Rolle’s Theorem, there exists at least one point ‘c’ in the open interval (a, b) such that:
f ‘(c) = 0
We can visualize Rolle’s theorem from the figure(1)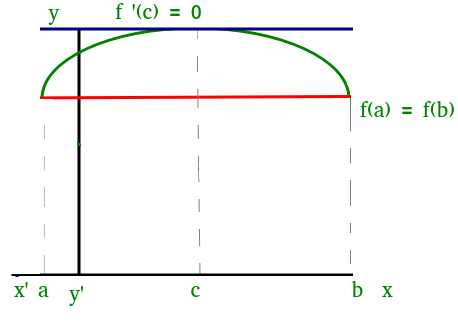 Figure(1)
Figure(1)
In the above figure the function satisfies all three conditions given above. So, we can apply Rolle’s theorem, according to which there exists at least one point ‘c’ such that:
f ‘ (c) = 0
which means that there exists a point at which the slope of the tangent at that is equal to 0. We can easily see that at point ‘c’ slope is 0.
Similarly, there could be more than one points at which slope of tangent at those points will be 0. Figure(2) is one of the example where exists more than one point satisfying Rolle’s theorem.
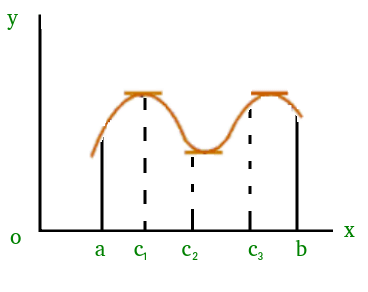 Figure(2)
Figure(2)
|
65 videos|129 docs|94 tests
|
FAQs on Mean Value Theorem - Engineering Mathematics - Engineering Mathematics
| 1. What is Cauchy’s Mean Value Theorem? |  |
| 2. What is Lagrange’s Mean Value Theorem? |  |
| 3. What is Rolle’s Mean Value Theorem? |  |
| 4. How are Cauchy’s, Lagrange’s, and Rolle’s Mean Value Theorems related? |  |
| 5. How are the Mean Value Theorems used in real-life applications? |  |






















