Metals, Semiconductors and Insulators | Modern Physics for IIT JAM PDF Download
Metals, Semiconductors and Insulators
Every solid has its own characteristic energy band structure. This variation in band structure is responsible for the wide range of electrical characteristics observed in various materials. The diamond band structure for example, can give a good picture of why carbon in the diamond lattice is a good insulator. To reach such a conclusion, we must consider the properties of completely filled and completely empty energy bands in the current conduction process. Before discussing the mechanisms of current flow in solids further, we can observe here that for electrons to experience acceleration in an applied electric field, they must be able to move into new energy states. This implies there must be empty states (allowed energy states which are not already occupied by electrons) available to the electrons. For example, if relatively few electrons reside in an otherwise empty band, ample unoccupied states are available into which the electrons can move. On the other hand, the diamond structure is such that the valence band is completely filled with electrons at 0K and the conduction band is empty. There can be no charge transport within the valence band, since no empty states are available into which electrons can move. There are no electrons in the conduction band, so no charge transport can take place there either. Thus carbon in the diamond structure has a high resistivity typical of insulators. Semiconductor materials at 0K have basically the same structure as insulators-a filled valence band separated from an empty conduction band by a band gap containing no allowed energy states (Figure). The difference lies in the size of the band gap Eg which is much smaller in semiconductors than in insulators. For example, the semiconductor Si has a band gap of about 1.1 eV compared with 5 eV for diamond. The relatively small band gaps of semiconductors allow for excitation of electrons from the lower (valence) band to the upper (conduction) band by reasonable amounts of thermal or optical energy. For example, at room temperature a semiconductor with a 1 eV band gap will have a significant number of electrons excited thermally across the energy gap into the conduction band whereas an insulator with Eg = 10 eV will have a negligible number of such excitations. Thus an important difference between semiconductors and insulators is that the number of electrons available for conduction can be increased greatly in semiconductors by thermal or optical energy.
In metals the bands either overlap or are only partially filled. Thus electrons and empty energy states are intermixed within the bands so that electrons can move freely under the influence of an electric field. As expected from the metallic band structures, metals have a high electrical conductivity.
Direct and Indirect Semiconductors
When quantitative calculations are made of band structures, a single electron is assumed to travel through a perfectly periodic lattice. The wave function of the electron is assumed to be in the form of a plane wave moving, for example, in the x -direction with propagation constant k , also called a wave vector. The space-dependent wave function for the electron is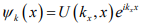
where the function U(kx x) modulates the wave function according to the periodicity of the lattice.
In such a calculation, allowed values of energy can be plotted vs. the propagation constant k . Since the periodicity of most lattices is different in various directions, the (E k), diagram must be plotted for the various crystal directions and the full relationship between E and k is a complex surface which should be visualized in three dimensions.
The band structure of GaAs has a minimum in the conduction band and a maximum in the valence band for the same k value (k = 0). On the other hand, Si has its valence band maximum at a different value of k than its conduction band minimum. Thus an electron making a smallest energy transition from the conduction band to the valence band in GaAs can do so without a change in k value; on the other hand a transition from the minimum point in the Si conduction band to the maximum point of the valence band requires some change in k . Thus there are two classes of semiconductor energy bands direct and indirect (Figure). We can show that an indirect transition involving a change in k requires a change of momentum for the electron.
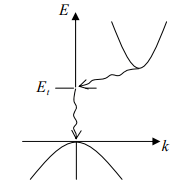
(a) Direct (b) Indirect
Electron and Hole Concentrations at Equilibrium
The Fermi distribution function can be used to calculate the concentrations of electrons and holes in a semiconductor, if the densities of available states in the valence and conduction bands are known. For example, the concentration of electrons in the conduction band is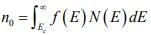
where N(E) dE is the density of states (cm-3) in the energy range dE . The subscript 0 used with the electron and hole concentration symbols (n0 , p0) indicates equilibrium conditions. The number of electrons per unit volume in the energy range dE is the product of the density of states and the probability of occupancy f (E) . Thus the total electron concentration is the integral over the entire conduction band. The function N (E) can be calculated by using quantum mechanics and the Pauli Exclusion Principle.
Since N (E) is proportional to E1/2, so the density of states in the conduction band increases with electron energy. On the other hand, the Fermi function becomes extremely small for large energies. The result is that the product f(E)N(E) decreases rapidly above Ec and very few electrons occupy energy states far above the conduction band edge. Similarly, the probability of finding an empty state (hole) in the valence band [1- f(E)] decreases rapidly below Ev and most holes occupy states near the top of the valence band. This effect is demonstrated in figure, which shows the density of available states, the Fermi function, and the resulting number of electrons and holes occupying available energy states in the conduction and valence bands at thermal equilibrium (i.e., with no excitations except thermal energy). For holes, increasing energy points down, since the E scale refers to electron energy.
Figure: Schematic band diagram, density of states, Fermi-Dirac distribution, and the carrier concentrations for (a) intrinsic, (b) n-type, and (c) p-type semiconductors at thermal equilibrium. The result of the integration of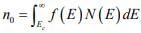 is the same as that obtained if we represent the entire distributed electron states in the conduction band by an effective density of states Nc located at the conduction band edge Ec . Therefore, the conduction band electron concentration is simply the effective density of states at Ec times the probability of occupancy at Ec
is the same as that obtained if we represent the entire distributed electron states in the conduction band by an effective density of states Nc located at the conduction band edge Ec . Therefore, the conduction band electron concentration is simply the effective density of states at Ec times the probability of occupancy at Ec 
In this expression we assume the Fermi level EF lies at least several kT below the conduction band. Then the exponential term is large compared with unity and the Fermi function f (Ec) can be simplified as 
Since kT at room temperature is only 0.026 eV , this is generally a good approximation. For this condition the concentration of electrons in the conduction band is
The effective density of states 
Thus electron concentration increases as EF moves closer to the conduction band. By similar arguments, the concentration of holes in the valence band is  where Nc is the effective density of states in the valence band.
where Nc is the effective density of states in the valence band.
The probability of finding an empty state at Ev is, 
for EF larger than Ev by several kT .
From these equations, the concentration of holes in the valence band is
The effective density of states in the valence band Nv = 2
Thus hole concentration increases as EF moves closer to the valence band. The electron and hole concentrations predicted by above equations are valid whether the material is intrinsic or doped, provided thermal equilibrium is maintained. Thus for intrinsic material, EF lies, at some intrinsic level Ei near the middle of the band gap, and the intrinsic electron and hole concentrations are
Note: The intrinsic level Ei is the middle of the band gap 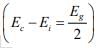 , if the effective densities of states Nc and Nc are equal. There is usually some difference in effective mass for electrons and holes, however, and Nc and Nc are slightly different. The product of n0 and po at equilibrium is a constant for a particular material and temperature, even if the doping is varied:
, if the effective densities of states Nc and Nc are equal. There is usually some difference in effective mass for electrons and holes, however, and Nc and Nc are slightly different. The product of n0 and po at equilibrium is a constant for a particular material and temperature, even if the doping is varied:
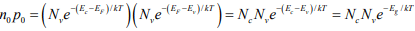

The intrinsic electron and hole concentrations are equal (since the carriers are created in pairs),ni = pi ; thus the intrinsic concentration is 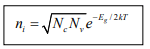
Law of Mass Action
The constant product of electron and hole concentrations can be written conveniently as 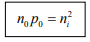 For n-type material the minority concentration (holes)
For n-type material the minority concentration (holes)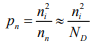 where ND is donor ion concentration.
where ND is donor ion concentration.
For p-type material the minority concentration (electrons)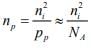 where NA is acceptor ion concentration.
where NA is acceptor ion concentration.
Another convenient way of writing electron and hole concentration is
This form of the equation indicates directly that the electron concentration is ni when EF is at the intrinsic level Ei and that no increases exponentially as the Fermi level moves away from Ei toward the conduction band. Similarly, the hole concentration po varies from ni to larger values as EF moves from Ei, toward the valence band. Since these equations reveal the qualitative features of carrier concentration so directly, they are particularly convenient to remember.
Electrons and Holes
As the temperature of a semiconductor is raised from 0K , some electrons in the valence band receive enough thermal energy to be excited across the band gap to the conduction band. The result is a material with some electrons in an otherwise empty conduction band and some unoccupied states in an otherwise filled valence band (Figure). For convenience, an empty state in the valence band is referred to as a hole. If the conduction band electron and the hole are created by the excitation of a valence band electron to the conduction band, they are called an electron-hole pair (abbreviated EHP).
After excitation to the conduction band, an electron is surrounded by a large number of unoccupied energy states. For example, the equilibrium number of electron-hole pairs in pure Si at room temperature is only about 1010 EHP cm3 , compared to the Si atom density of more than 1022 atoms/cm3. Thus the few electrons in the conduction band are free to move about via the many available empty states.
Effective Mass
The electrons in a crystal are not completely free, but instead interact with the periodic potential of the lattice. As a result, their “wave-particle” motion can-not be expected to be the same as for electrons in free space. Thus, in applying the usual equations of electrodynamics to charge carriers in a solid, we must use altered values of particle mass. In doing so, we account for most of the influences of the lattice, so that the electrons and holes can be treated as “almost free” carriers in most computations. The calculation of effective mass must take into account the shape of the energy bands in three-dimensional k -space, taking appropriate averages over the various energy bands.
|
52 videos|44 docs|15 tests
|
FAQs on Metals, Semiconductors and Insulators - Modern Physics for IIT JAM
| 1. What are metals, semiconductors, and insulators? |  |
| 2. What are some examples of metals, semiconductors, and insulators? |  |
| 3. How do metals, semiconductors, and insulators differ in terms of their band structure? |  |
| 4. How are metals, semiconductors, and insulators utilized in everyday life? |  |
| 5. Can materials switch between being a metal, semiconductor, or insulator? |  |
















