Minimum Spanning Tree | Algorithms - Computer Science Engineering (CSE) PDF Download
What is Minimum Spanning Tree?
Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected, undirected graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.How many edges does a minimum spanning tree have?
A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.
Kruskal’s algorithm
Below are the steps for finding MST using Kruskal’s algorithm:
- Sort all the edges in non-decreasing order of their weight.
- Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it.
- Repeat step#2 until there are (V-1) edges in the spanning tree.
The algorithm is a Greedy Algorithm. The Greedy Choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far. Let us understand it with an example: Consider the below input graph.
The graph contains 9 vertices and 14 edges. So, the minimum spanning tree formed will be having (9 – 1) = 8 edges.
After sorting:
Now pick all edges one by one from the sorted list of edges
1. Pick edge 7-6: No cycle is formed, include it.
2. Pick edge 8-2: No cycle is formed, include it. 3. Pick edge 6-5: No cycle is formed, include it.
3. Pick edge 6-5: No cycle is formed, include it. 4. Pick edge 0-1: No cycle is formed, include it.
4. Pick edge 0-1: No cycle is formed, include it.

5. Pick edge 2-5: No cycle is formed, include it. 6. Pick edge 8-6: Since including this edge results in the cycle, discard it.
6. Pick edge 8-6: Since including this edge results in the cycle, discard it.
7. Pick edge 2-3: No cycle is formed, include it.
8. Pick edge 7-8: Since including this edge results in the cycle, discard it.
9. Pick edge 0-7: No cycle is formed, include it.
10. Pick edge 1-2: Since including this edge results in the cycle, discard it.
11. Pick edge 3-4: No cycle is formed, include it.
Since the number of edges included equals (V – 1), the algorithm stops here.
Below is the implementation of the above idea:
C








Java






Python




C#







C++







Output
Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimum Cost Spanning Tree: 19
Time Complexity: O(ElogE) or O(ElogV). Sorting of edges takes O(ELogE) time. After sorting, we iterate through all edges and apply the find-union algorithm. The find and union operations can take at most O(LogV) time. So overall complexity is O(ELogE + ELogV) time. The value of E can be at most O(V2), so O(LogV) is O(LogE) the same. Therefore, the overall time complexity is O(ElogE) or O(ElogV)
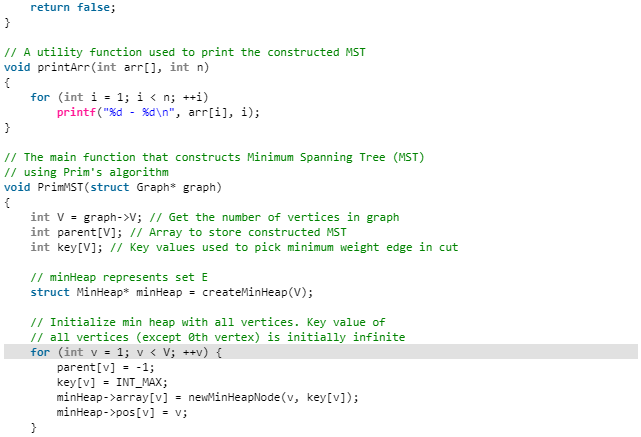
Prim's Algorithm
It starts with an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, the other set contains the vertices not yet included. At every step, it considers all the edges that connect the two sets, and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST.
A group of edges that connects two set of vertices in a graph is called cut in graph theory. So, at every step of Prim’s algorithm, we find a cut (of two sets, one contains the vertices already included in MST and other contains rest of the vertices), pick the minimum weight edge from the cut and include this vertex to MST Set (the set that contains already included vertices).
How does Prim’s Algorithm Work?
The idea behind Prim’s algorithm is simple, a spanning tree means all vertices must be connected. So the two disjoint subsets (discussed above) of vertices must be connected to make a Spanning Tree. And they must be connected with the minimum weight edge to make it a Minimum Spanning Tree.
Algorithm
1. Create a set mstSet that keeps track of vertices already included in MST.
2. Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first.
3. While mstSet doesn’t include all vertices
….a) Pick a vertex u which is not there in mstSet and has minimum key value.
….b) Include u to mstSet.
….c) Update key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v
The idea of using key values is to pick the minimum weight edge from cut. The key values are used only for vertices which are not yet included in MST, the key value for these vertices indicate the minimum weight edges connecting them to the set of vertices included in MST.
Let us understand with the following example: The set mstSet is initially empty and keys assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with the minimum key value. The vertex 0 is picked, include it in mstSet. So mstSet becomes {0}. After including to mstSet, update key values of adjacent vertices. Adjacent vertices of 0 are 1 and 7. The key values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their key values, only the vertices with finite key values are shown. The vertices included in MST are shown in green color.
The set mstSet is initially empty and keys assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with the minimum key value. The vertex 0 is picked, include it in mstSet. So mstSet becomes {0}. After including to mstSet, update key values of adjacent vertices. Adjacent vertices of 0 are 1 and 7. The key values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their key values, only the vertices with finite key values are shown. The vertices included in MST are shown in green color. Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.
Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8. Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (1 and 7 respectively).
Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (1 and 7 respectively). Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.
Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated. We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.
We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.
How to implement the above algorithm?
We use a boolean array mstSet[] to represent the set of vertices included in MST. If a value mstSet[v] is true, then vertex v is included in MST, otherwise not. Array key[] is used to store key values of all vertices. Another array parent[] to store indexes of parent nodes in MST. The parent array is the output array which is used to show the constructed MST.
C++



C



Java



Python


C#




Output:
Time Complexity of the above program is O(V^2). If the input graph is represented using adjacency list, then the time complexity of Prim’s algorithm can be reduced to O(E log V) with the help of binary heap. Please see Prim’s MST for Adjacency List Representation for more details.
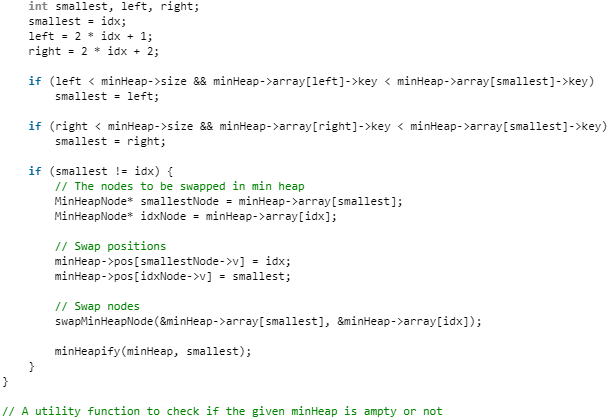
Finding MST using Min Heap
Min Heap is used as a priority queue to get the minimum weight edge from the cut. Min Heap is used as time complexity of operations like extracting minimum element and decreasing key value is O(LogV) in Min Heap.
Following are the detailed steps:
1. Create a Min Heap of size V where V is the number of vertices in the given graph. Every node of min heap contains vertex number and key value of the vertex.
2. Initialize Min Heap with first vertex as root (the key value assigned to first vertex is 0). The key value assigned to all other vertices is INF (infinite).
3. While Min Heap is not empty, do following
…..a) Extract the min value node from Min Heap. Let the extracted vertex be u.
…..b) For every adjacent vertex v of u, check if v is in Min Heap (not yet included in MST). If v is in Min Heap and its key value is more than weight of u-v, then update the key value of v as weight of u-v.
Let us understand the above algorithm with the following example: Initially, key value of first vertex is 0 and INF (infinite) for all other vertices. So vertex 0 is extracted from Min Heap and key values of vertices adjacent to 0 (1 and 7) are updated. Min Heap contains all vertices except vertex 0.
Initially, key value of first vertex is 0 and INF (infinite) for all other vertices. So vertex 0 is extracted from Min Heap and key values of vertices adjacent to 0 (1 and 7) are updated. Min Heap contains all vertices except vertex 0.
The vertices in green color are the vertices included in MST.
Since key value of vertex 1 is minimum among all nodes in Min Heap, it is extracted from Min Heap and key values of vertices adjacent to 1 are updated (Key is updated if the a vertex is in Min Heap and previous key value is greater than the weight of edge from 1 to the adjacent). Min Heap contains all vertices except vertex 0 and 1.
Since key value of vertex 7 is minimum among all nodes in Min Heap, it is extracted from Min Heap and key values of vertices adjacent to 7 are updated (Key is updated if the a vertex is in Min Heap and previous key value is greater than the weight of edge from 7 to the adjacent). Min Heap contains all vertices except vertex 0, 1 and 7.
Since key value of vertex 6 is minimum among all nodes in Min Heap, it is extracted from Min Heap and key values of vertices adjacent to 6 are updated (Key is updated if the a vertex is in Min Heap and previous key value is greater than the weight of edge from 6 to the adjacent). Min Heap contains all vertices except vertex 0, 1, 7 and 6.
The above steps are repeated for rest of the nodes in Min Heap till Min Heap becomes empty
C++









Java





Python






Output:
0 - 1
5 - 2
2 - 3
3 - 4
6 - 5
7 - 6
0 - 7
2 - 8
Time Complexity: The time complexity of the above code/algorithm looks O(V^2) as there are two nested while loops. If we take a closer look, we can observe that the statements in inner loop are executed O(V+E) times (similar to BFS). The inner loop has decreaseKey() operation which takes O(LogV) time. So overall time complexity is O(E+V)*O(LogV) which is O((E+V)*LogV) = O(ELogV) (For a connected graph, V = O(E))
Applications of Minimum Spanning Tree Problem
Minimum Spanning Tree (MST) problem: Given connected graph G with positive edge weights, find a min weight set of edges that connects all of the vertices.
MST is fundamental problem with diverse applications.
Network design.
- telephone, electrical, hydraulic, TV cable, computer, road
The standard application is to a problem like phone network design. You have a business with several offices; you want to lease phone lines to connect them up with each other; and the phone company charges different amounts of money to connect different pairs of cities. You want a set of lines that connects all your offices with a minimum total cost. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money.
Approximation algorithms for NP-hard problems.
- traveling salesperson problem, Steiner tree
A less obvious application is that the minimum spanning tree can be used to approximately solve the traveling salesman problem. A convenient formal way of defining this problem is to find the shortest path that visits each point at least once.
Note that if you have a path visiting all points exactly once, it’s a special kind of tree. For instance in the example above, twelve of sixteen spanning trees are actually paths. If you have a path visiting some vertices more than once, you can always drop some edges to get a tree. So in general the MST weight is less than the TSP weight, because it’s a minimization over a strictly larger set.
On the other hand, if you draw a path tracing around the minimum spanning tree, you trace each edge twice and visit all points, so the TSP weight is less than twice the MST weight.
Therefore this tour is within a factor of two of optimal.
1. Indirect applications
- max bottleneck paths
- LDPC codes for error correction
- image registration with Renyi entropy
- learning salient features for real-time face verification
- reducing data storage in sequencing amino acids in a protein
- model locality of particle interactions in turbulent fluid flows
- autoconfig protocol for Ethernet bridging to avoid cycles in a network
2. Cluster analysis
- k clustering problem can be viewed as finding an MST and deleting the k-1 most expensive edges.
|
81 videos|80 docs|33 tests
|
FAQs on Minimum Spanning Tree - Algorithms - Computer Science Engineering (CSE)
| 1. What is Prim's Algorithm used for in computer science engineering? |  |
| 2. How does Prim's Algorithm work in finding the MST using Min Heap? |  |
| 3. Why is a Min Heap used in Prim's Algorithm for finding the MST? |  |
| 4. What is the time complexity of Prim's Algorithm when using a Min Heap? |  |
| 5. Can Prim's Algorithm be used for directed graphs? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















