Mixtures and Alligations: Solved Examples | Quantitative Aptitude (Quant) - CAT PDF Download
Mixtures & Alligation
- As the dictionary meaning of Alligation (mixing), we will deal with problems related to mixing of different compounds or quantities. The concept of alligation and weighted average are the same.
- When two or more quantities are mixed together in different ratios to form a mixture, then ratio of the quantities of the two constituents is given by the following formulae:


- Gives us the ratio of quantities in which the two ingredients should be mixed to get the mixture.
Example.1: A sum of Rs 39 was divided among 45 boys and girls. Each girl gets 50 paise, whereas a boy gets one rupee. Find the number of boys and girls.
- Average amount of money received by each =
- Amount received by each girl = 50 paise = Rs
- Amount received by each boy = Re. 1
Number of girls = 45 – 33 = 12.
Important Funda
- Always identify the ingredients as cheaper & dearer to apply the alligation rule.
In the alligation rule, the variables c, d & m may be expressed in terms of percentages (e.g. A 20% mixture of salt in water), fractions (e.g. two-fifth of the solution contains salt) or proportions (e.g. A solution of milk and water is such that milk : Water = 2 : 3).- The important point is to remember is that c & d may represent pure ingredients or mixtures.
Mixing a pure component into a solution
Example.2: A jar contains a mixture of two liquids A and B in the ratio 4 : 1. When 10 litres of the liquid B is poured into the jar, the ratio becomes 2: 3. How many litres of liquid A were contained in the jar?
Method 1: (weighted average or equation method)
- Let the quantities of A & B in the original mixture be 4x and x litres.
- According to the question
12x = 2x + 20
⇒ 10x = 20
⇒ x = 2- The quantity of A in the original mixture = 4x = 4 × 2 = 8 litres.
Method 2: (Alligation with composition of B)
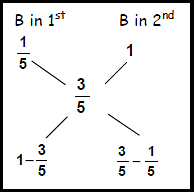
- The average composition of B in the first mixture is 1/5.
- The average composition of B in the second mixture = 1
- The average composition of B in the resultant mixture = 3/5
- Hence applying the rule of Alligation we have
[1 – (3/5)]/[(3/5) – (1/5)] = (2/5)/(2/5) = 1
So, initial quantity of mixture in the jar = 10 litres.
And, quantity of A in the jar = (10 × 4)/5 = 8 litres.
Method 3: (Alligation with percentage of B)
- The percentage of B in 1st mixture = 20%
- The percentage of B in 2nd mixture = 100%
- The percentage of B in Final Mixture = 60%
- By rule of allegation we have
Volume 1st : Volume 2nd = (100% - 60%) : (60% - 20%)
V1 : V2 = 1 : 1
Volume of mixture 1st = 10 litres
Volume of A in mixture 1st = 80% of 10 litres = 8 litres. Answer
Removal and Replacement

Example.3: Nine litres of solution are drawn from a cask containing water. It is replaced with a similar quantity of pure milk. This operation is done twice. The ratio of water to milk in the cask now is 16 : 9. How much does the cask hold?
- Let there be x litres in the cask
- After n operations:
(1 – 9/x)2 = 16/25
∴ x = 45 litres.
Example.4: There are two containers A and B of milk solution. The ratio of milk and water in container A is 3 : 1 and in container B, it is 4 : 1. How many liters of container B solution has to be added to 20. lts of container ‘A’ solution such that in the resulting solution; the ratio of milk to water should be 19 : 6?
- In container A, the part of milk =
- It is given 20 lts of container A is added. So, the quantity of container B should be 5 lts.
Example.5: There are two alloys A and B. Alloy A contains zinc, copper and silver, as 80% 15% and 5% respectively, whereas alloy B also contains the same metals with percentages 70%, 20%, 10% respectively. If these two alloys are mixed such that the resultant will contain 8% silver, what is the ratio of these three metals in the resultant alloy?
- Since the resultant alloy contains 8% silver, first we will find, in what ratio these two alloys A and B were mixed to form the resultant.
- Then the resultant zinc percentage is
- So, copper percentage = 100 – (74 + 8) = 18
∴ The ratio of these metals = 74 : 18 : 8 = 37 : 9 : 4.
Example.6: The cost of an apple is directly proportional to square of its weight in a fruit bazaar. Two friends A and B went there to purchase apples. A got exactly 5 apples per kg and each apple is of same weight. Where as B got exactly 4 apples per kg each weight is exactly same. If B paid Rs. 10 more than A per kg apples, what is the cost of an apple which weighs 1 kg?
- It is given cost ∝ (weight)2
⇒ c = k w2.- A got 5 apples per kg and each apple is of same weight. ⇒ Each apple is 200 gm. = 1/5 kg.
|
196 videos|131 docs|110 tests
|
FAQs on Mixtures and Alligations: Solved Examples - Quantitative Aptitude (Quant) - CAT
| 1. What is the concept of mixtures and alligation? |  |
| 2. How is mixtures and alligation useful in real life? |  |
| 3. Can you explain the basic formula or equation used in mixtures and alligation? |  |
| 4. How can mixtures and alligation be applied to solve practical problems? |  |
| 5. Can you provide an example of mixtures and alligation in a real-life scenario? |  |

|
Explore Courses for CAT exam
|

|