Mixtures and Averages Questions for CAT with Answers PDF
Q1. A 20 litre mixture of milk and water contains milk and water in the ratio 3 : 2. 10 litres of the mixture is removed and replaced with pure milk and the operation is repeated once more. At the end of the two removal and replacement, what is the ratio of milk and water in the resultant mixture?
1. 17 : 3
2. 9 : 1
3. 3 : 17
4. 5 : 3
Answer. 9 : 1
Explanation.
The 20 litre mixture contains milk and water in the ratio of 3 : 2. Therefore, the mixture contains 12 litres of milk and 8 litres of water.
Therefore, there will be 6 litres of milk and 4 litres of water left in the container.
It is then replaced with pure milk of 10 litres. Now the container will have 16 litres of milk and 4 litres of water.
The container will have 8 litres of milk and 2 litres of water in it.
Now 10 litres of pure milk is added. Therefore, the container will have 18 litres of milk and 2 litres of water in it at the end of the second step.
We are essentially replacing water in the mixture with pure milk.
Let WO be the amount of water in the mixture originally = 8 litres.
Let WR be the amount of water in the mixture after the replacements have taken place.
Then,
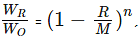 where R is the amount of the mixture replaced by milk in each of the steps, M is the total volume of the mixture and n is the number of times the cycle is repeated.
where R is the amount of the mixture replaced by milk in each of the steps, M is the total volume of the mixture and n is the number of times the cycle is repeated.Hence,
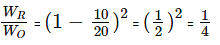
Therefore,
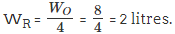
WR is the quantity of water in the mixture after the process is done twice.
So, the final quantity of water in the 20-litre mixtures is 2 litres.
Hence, the mixture will have 18 litres of milk and 2 litres of water.
1. 1 : 2 : 4
2. 3 : 7 : 6
3. 1 : 4 : 2
4. None of these
Answer. 1 : 4 : 2
Explanation.
Step 1: Compute cost of 1 kg of the mixture
The resultant mixture is sold at a profit of 20%. The selling price is Rs.96/kg
i.e., cost + 20% of cost = 1.2 (cost) = Rs.96
⇒ cost of the mixture = 96/1.2 = Rs.80/kg.
Let the three variants be A, B, and C and let their cost per kg be Rs.60, Rs.75 and Rs.100 respectively.
The mean price falls between B and C.
Hence the following method should be used to find the ratio in which the 3 variants should be mixed.
Step 2: Find out the ratio of QA : QC using alligation rule
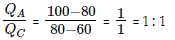
Step 3: Find out the ratio of QB : QC using alligation rule
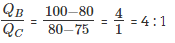
Step 4: QC, the resultant ratio of variant 'C' can be found by adding the value of QC in step 1 and step 2 = 1 + 1 = 2.
The resultant ratio QA : QB : QC :: 1 : 4 : 2.
Note.
However, if you try and solve this problem using the above method, you will end up spending more than 2, and may be 3 minutes on this question, which is not wise way to manage time in the test.
The best way to solve a problem of this kind in CAT or TANCET is to go from the answer choices as shown below.
Let us go with the correct answer. They are mixed in the ratio 1 : 4 : 2.
1 kg of variant A at Rs.60 is mixed with 4 kg of variant B at Rs.75 and 2 kg of variant C at Rs.100.
The total cost for 7 kg of the mixture = 60 + (4 * 75) + (2 * 100) = 60 +300 + 200 = Rs.560.
Cost per kg of the mixture = 560/7 = Rs.80 which matches the cost we arrrived at in the Step 1.
Even assuming that you hit upon the right answer as the last choice, you will still be better of by back substituting choices for this question.
1. 1 kg
2. 5 kg
3. 3 kg
4. 6 kg
Explanation.
Step 1: Compute cost price of 1 kg of mixture.
The selling price of mixture is Rs.30/kg and the merchant makes a profit of 20%.
If the cost of 1 kg of the mixture is c, c + 20% of c = 1.2 c = selling price
The cost price of the mixture, c = 30/1.2 = Rs.25/kg.
Step 2: Find the ratio in which the 3 variants are mixed
The three variants are mixed to obtain a mixture that costs Rs.25 /kg.
Variant A costs Rs.20/kg, variant B costs Rs.24/kg and variant C costs Rs.30/kg. The mean price of the mixture falls between the costs of B and C.
Step 2.1: Find out the ratio QA : QC using alligation rule.
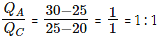
Step 2.2: Find out the ratio QB : QC using alligation rule.
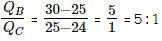
Step 2.3: QC is common to both the ratios. The value of QC is found by adding the value of QC in step 2.1 and step 2.2 = 1 + 1 = 2
Therefore, the required ratio = 1 : 5 : 2
If there are 2 kgs of the third variant in the mixture, then there will be 5 kgs of the second variant in the mixture.
Note: This question is a time consuming question. If you can revisit questions in the test, mark it for review and proceed to the next one. Else, skip this question without batting an eyelid.
Q4. How many litres of water should be added to a 30 litre mixture of milk and water containing milk and water in the ratio of 7 : 3 such that the resultant mixture has 40% water in it?
1. 7 litres
2. 10 litres
3. 5 litres
4. None of these
Answer. 5 litres
Explanation. 30 litres of the mixture has milk and water in the ratio 7 : 3. i.e. the solution has 21 litres of milk and 9 litres of water.
When you add more water, the amount of milk in the mixture remains constant at 21 litres. In the first case, before addition of further water, 21 litres of milk accounts for 70% by volume. After water is added, the new mixture contains 60% milk and 40% water.
Therefore, the 21 litres of milk accounts for 60% by volume.
Hence, 100% volume = 21/0.6 = 35 litres.
We started with 30 litres and ended up with 35 litres. Therefore, 5 litres of water was added.
Q5. How many kg of Basmati rice costing Rs.42/kg should a shopkeeper mix with 25 kg of ordinary rice costing Rs.24 per kg so that he makes a profit of 25% on selling the mixture at Rs.40/kg?
1. 20 kg
2. 12.5 kg
3. 16 kg
4. 200 kg
Answer. 20 kg
Explanation. Let the amount of Basmati rice being mixed be x kgs. As the trader makes 25% profit by selling the mixture at Rs.40/kg, his cost /kg of the mixture = Rs.32/kg.
i.e. (x * 42) + (25 * 24) = 32 (x + 25)
⇒ 42x + 600 = 32x + 800
⇒ 10x = 200 or x = 20 kgs
Q6. How many litres of a 12 litre mixture containing milk and water in the ratio of 2 : 3 be replaced with pure milk so that the resultant mixture contains milk and water in equal proportion?
1. 4 litres
2. 2 litres
3. 1 litre
4. 1.5 litres
Answer. 2 litres
Explanation.
That is 4.8 litres of milk and 7.2 litres of water.
We are replacing the mixture with pure milk so that the amount of milk and water in the mixture is 50% and 50%.
So, we will end up with 6 litres of milk and 6 litres of water.
Water gets reduced by 1.2 litres.
To remove 1.2 litres of water from the original mixture containing 60% water, we need to remove 1.2/0.6 litres of the mixture = 2 litres.
Q7. A sample of x litres from a container having a 60 litre mixture of milk and water containing milk and water in the ratio of 2 : 3 is replaced with pure milk so that the container will have milk and water in equal proportions. What is the value of x?
1. 6 litres
2. 10 litres
3. 30 litres
4. None of these
Answer. 10 litres
Explanation.
Let us solve this question by back substituting answer choices.
The rigorous method of solving is outlined in the previous question on removing and replacing mixtures.
The mixture of 60 litres has milk and water in the ratio 2 : 3
i.e., 24 litres of milk and 36 litres of water.When x litres of the mixture is removed, 0.4 x litres of milk and 0.6 x litres of water are removed from it.Take choice (2). According to this choice, x = 10.
So, 10 litres of the mixture is removed.
4 litres of milk and 6 litres of water are removed.
Therefore, there will be 20 litres of milk and 30 litres of water in the container.
Subsequently, when 10 litres of milk is added, the mixture will contain 30 litres of milk and 30 litres of water - i.e. milk and water are in equal proportion.
Q8. A farmer counted the heads of the animals / birds in the farm and found it to be 80. When he counted the legs he found it to be 260. If the farm had either pigeons or horses and nothing else, how many horses were there in the farm? In the farm, each horse had four legs and each pigeon had two legs.
1. 40
2. 30
3. 50
4. 60
Answer. 50
Explanation.
The count of heads gives the total number of animals / birds as each animal / bird has one head.
Let the number of horses be x.
The remaining will be pigeons. The number of pigeons = (80 - x).
Each pigeon has 2 legs and each horse has 4 legs.
Therefore, total number of legs = 4x + 2(80 - x) = 260
⇒ 4x + 160 - 2x = 260
⇒ 2x = 100
⇒ x = 50.
x is the number of horses. The number of horses in the farm is 50.
Q9. From a cask of milk containing 30 litres, 6 litres are drawn out and the cask is filled up with water. If the same process is repeated a second, then a third time, what will be the number of litres of milk left in the cask?
1. 0.512 liters
2. 12 liters
3. 14.38 liters
4. 15.36 liters
Answer. 15.36 liters
Explanation.
The problem can be solved by brute force of removing and replacing 6 litres each time and finding the quantity of milk and water after each iteration. Finally, after step 3, we will get to the answer. But it is cumbersome to do that.
The question can be solved more effectively. Let us use that method to solve this question.
Let us find the fraction of milk left after nth operation.
Fraction of milk in the cask after the nth iteration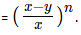
'x' is initial quantity of milk in the cask 'y' is the quantity of milk drawn out in each iteration and 'n' is the number of iterations.
Fraction of milk left after the 3rd iteration 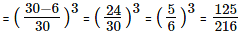
∴ the quantity of milk in the cask after the 3rd iteration 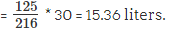
Q10. A 20 litres mixture of milk and water comprising 60% pure milk is mixed with "x" litres of pure milk. The new mixture comprises 80% milk. What is the value of "x"?
1. 40 litres
2. 20 litres
3. 8 litres
4. 16 litres
Answer. 20 litres
Explanation.
The quantity of the initial mixture of milk and water is 20 litres.
Out of the 20 litres, 60% is pure milk. i.e., 12 litres is milk and the remaining 8 litres is water.
When "x" litres of pure milk is added, we will have (12 + x) litres of milk in the new mixture.
And there will be 20 + x litres of the new mixture.
The question states that (12 + x) litres of milk accounts for 80% of (20 + x) litres of the mixture.
Therefore, 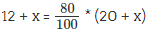
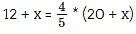
5(12 + x) = 4(20 +x)
60 + 5x = 80 + 4x
x = 20 litres
|
191 videos|131 docs|110 tests
|
FAQs on Mixtures and Averages Questions for CAT with Answers PDF
| 1. What is a mixture? |  |
| 2. What is an allegation in mixtures? |  |
| 3. How can mixtures and allegations be used in real-life situations? |  |
| 4. What is the method to solve mixture and allegation problems? |  |
| 5. Can mixtures and allegations be used to solve problems other than finding ratios? |  |

|
Explore Courses for CAT exam
|

|


















