Concept of Calendars | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Importance of Calendar Based Questions
Studying the "Calendars" topic is crucial for logical reasoning in competitive exams as it involves complex logical analysis, enhancing problem-solving skills. With 2 to 4 problems commonly appearing in competitive exams, a strong grasp of calendar concepts is essential for maximizing scores. Additionally, it requires the application of mathematical concepts, making it a multifaceted and important component of logical reasoning preparation.
What is a Calendar?
A Calendar is a chart or series of pages showing the days, weeks, and months of a particular year, or giving particular seasonal information.

Basic Structure of a Calendar
- Ordinary year: Any year in which 365 days is called an ordinary year.Ex: 1879, 2009, 2019, etc.
- Leap year: Any year which has 366 days is called a leap year.Ex: 2012, 2016 2020 etc.
- The division of the number 365 by 7 gives the quotient 52 and the remainder 1 which indicates that an ordinary year has 52 weeks and one extra day. This extra day is referred to as an “odd day” throughout the calendar topics.
- A leap year has 366 days, the division of the number 366 by 7 gives the quotient 52 and the remainder 2. This indicates that a leap year has 52 weeks and 2 extra days. These two extra days are also referred to as “odd days”.
Concept of Odd Days
1. A number of odd days in a month
- January has 31 days, irrespective of whether it’s an ordinary year or a leap year. The division of the number 31 by 7 provides the remainder of 3 hence January has 3 odd days. On generalising, any month which has 31 days has 3 odd days and any month which has 30 days has 2 odd days. The only exception that happens is in the case of February.
- The February month of an ordinary year has 28 days, division of 28 by 7 provides zero as remainder. Hence, the number of odd days in February of an ordinary year will have 0 odd days and that of leap year will have 1 odd day as February in a leap year has 29 days.
The below table depicts the number of odd days in different months of a calendar year: - In an ordinary year, there are 365 days, which means 52 x 7 + 1, or 52 weeks and one day. This additional day is called an odd day. The concept of odd days is very important in calendars.
- In a century - i.e. 100 years, there will be 24 leap years and 76 non-leap years. This means that there will be 24 x 2 + 76 x 1 = 124 odd days. Since, 7 odd days make a week, to find out the net odd days, divide 124 by 7. The remainder is 5. This is the number of odd days in a century.
- You may memorize the following points related to the concepts of calendars to save time during the paper:
(i) 100 years give us 5 odd days as calculated above.
(ii) 200 years give us 5 x 2 = 10-7 (one week) => 3 odd days.
(iii) 300 years give us 5 x 3 = 15-14 (two weeks) => 1 odd day.
(iv) 400 years give us {5 x 4 + 1 (leap century)}-21} => 0 odd days. - Now, if we start from 1st January 0001 AD; for 0 odd days, the day will be Sunday; for 1 odd day, the day will be Monday; for 2 odd days, it will be Tuesday; for 3 odd days, it will be Wednesday and so on.
2. Counting of Odd Days
- 1 ordinary year = 365 days = (52 weeks + 1 day.)
1 ordinary year has 1 odd day - 1 leap year = 366 days = (52 weeks + 2 days)
1 leap year has 2 odd days - 100 years = 76 ordinary years + 24 leap year
= (76 x 1 + 24 x 2) odd days = 124 odd days
= (17 weeks + days) 5 odd days. - A number of odd days in 100 years = 5
- A number of odd days in 200 years = (5 x 2) 3 odd days.
- A number of odd days in 300 years = (5 x 3) 1 odd day.
- A number of odd days in 400 years = (5 x 4 + 1) 0 odd day.
- Similarly, each one of 800 years, 1200 years, 1600 years, 2000 years etc. has 0 odd days.

Concept of Leap Year
- Every 100th year starting from 1st AD is a non-leap year, but every 4th century year is a leap year.
- Any year divisible by 400 will be a leap year e.g.: 1200, 1600 and 2000. And the years 1800, 1900 will be non-leap years as they are divisible by 100, but not 400.
Evaluation of Leap Year
The leap year occurs every four years, most of the time, but there are scenarios where the gap between two leap years was 8 years instead of the regular 4 years.
Example: The year 1896 is a leap year. The next leap year comes in 1904 (1900 is not a leap year).
In order to make the investigation easier and faster, any year which is divisible by number 4 completely (remainder becomes zero) is considered as a leap year.
Example: 1888, 2012, 2016 are leap years as it’s completely divisible by 4. Years like 2009, 2019 etc. are not divisible by 4 completely hence they normal years.
An exception to note:
A year 700 is completely divisible by 4, but it is not considered as a leap year. For a century year, the logic follows that it should always be divisible by 400 not by 4. Even though the year 700 is divisible by 4 but not by 400. Hence, the year 700 cannot be considered as a leap year.
Example: 400, 800, 1200 etc. are leap years as they are divisible by 400 and years 300, 700, 100 etc. are not leap years as they are not divisible by 400.
What is the Ordinary Year?
Calendar Calculations
The year consists of 365 days, 5 hours, 48 minutes (52 weeks and 1 odd day). An extra day is added once in every fourth year which was called the leap year, which has 366 days (52 weeks and 2 odd days).
To find the day of any given date of the year, you need to understand the calendar calculations:
- 1st January 1 AD was Monday therefore; we must count days from Sunday. This means the 0th day was Sunday, so the 7th day was Sunday again, and so on and so forth.
- The day gets repeated after every seventh day (concept of a week), if today is Monday, then 28th day from now will also be Monday as it is a multiple of 7 (28/7 = 4, so four weeks). Here the 30 day will be calculated by 30/7, which is 4 weeks and 2 days, these two days are called odd days. With starting day as Monday and two odd days, the day will be Wednesday; this point is the most critical in calendars. The other of looking at it is since the 28th day is Monday, so the 30th day will be Wednesday. But you have to understand and use the concept of odd days as the question may be about thousands of years.
- In a normal year, there are 365 days so 52 weeks and 1 odd day, in a leap year there are 366 days so 52 weeks and 2 odd days.
- In 100 years there are 24 leap years and 76 normal years, so the number of odd days are 24(2) + 76 = 124, which is 17 weeks + 5 odd days, so 100 years have 5 odd days.
- In 200 years the number of odd days is twice the number in 100 years which is 10, which is one week and 3 odd days, so 200 years have 3 odd days. In 300 years, the number of odd days is 15, which is two weeks and 1 odd day, so 300 years have one odd day.
- 400 years is a leap year; similarly, the multiples of 400 also leap years.
- In 400 years, the number of odd days becomes 20 + 1(from the leap year), so total days are 21, which is three weeks and 0 odd days. In 400 years there are 0 odd days
Type 1 Problems: Finding the day when another day is given
Q1: If 17th march 2008 was Monday, what was 1st April 2012?
Sol: The total number of odd days from 17th March 2008 to 17th March 2012.
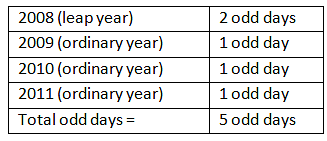
Since 17th march 2008 was Monday and 17th march 2012 is 5 days more than Monday. Then adding 5 odd days to Monday, we get Saturday. Hence 17th march to April 1st we have 15 days. Saturday+15=Sunday. Adding 15 days or (15 = 14+1) to Saturday, we get the answer as Sunday.
Q2: If today is Sunday, what will be the day on 7777th day?
Sol: If today is Sunday, then the 7th day from today will be Sunday.
Similarly, the 14th day, 21st day or 70th day or 700th day or 7000th day or 7777th day will be Sunday.
Hence, the answer is Sunday.
Type 2 Problems: Find the day when another day is not given
In this section, one has to find out the day of the week of a given date. There will no reference date or day has given here. One can make use of the concept of an odd day to find the answer.
Q1: What day of the week was 15th August 1947?
Sol: The date August 15th 1947 can be divided as follows for easy calculation:
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Note:- Do not write 47 years in the third section, it would indicate 47th year in that century is over.
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Now let’s find out the total number of odd days in each section:
Section 1: 1600 is a multiple of 400 years. 400 years have 0 odd days hence 1600 years should have 0 odd days.
Section 2: The second section 30 years will have 1 odd day. Kindly refer to “evaluation of odd days in a century” topic for clarification.
Section 3: This section has 46 years from 1901 to 1946, we know that an ordinary year has one odd day and a leap year has 2 odd days.
Let’s first calculate the total number of leap years from 1901 to 1946.
Division of 46 by 4 gives the quotient as 11, which indicates that from 1901 to 1946 we have 11 leap years. If there are 11 leap years among 46 years then remaining 35 years should be ordinary years. Hence, 35 ordinary years will have 35 odd days and 11 leap years will have 11*2 = 22 years.
The total number of odd days in 46 years will be 35+22 = 57 odd days. The division of 57 by 7 given the remainder as 1.This indicates from 1901 to 1946 there is only one odd day.
Section 4: It has months from January to August 15th. We have already calculated the total number of odd days in each month in the odd day’s section.
Since 1947 is not a leap year February had zero odd days.
Check the table below for a better understanding of the number of odd days in a month: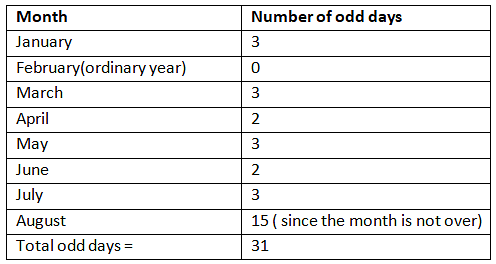
The total number of odd days is 31 which when divided by 7 gives the remainder 3. Hence, the total number of odd days in the year 1947 from January 1st to August 15th is 3.
Adding the total number of odd days of each section: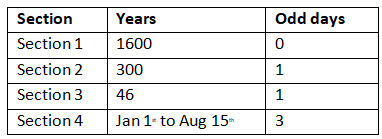
The total number of odd days = 0 + 1 + 1 + 3 = 5 = Friday. Hence, August 15th 1947 was Friday.
Type 3 Problems: Matching the Calendar
Question: Which year in the future will have the same calendar exactly as 2009?
(A) 2010
(B) 2013
(C) 2015
(D) 2017
Ans: (C)
So: If the total number of odd days between any years is zero or it’s a multiple of seven. Then, those two years will have the same calendar.
The total number of odd days is listed below: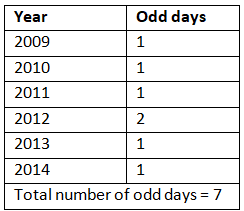
Hence, 2015 will have the same calendar as 2009. Option C is the correct answer.
Solved Examples
Example 1: What was the day on 9th February 1979?
- You know that in 1600 years, there will be 0 odd days. And in the next 300 years, there will be 1 odd day.
- From 1901 to 1978 we have 19 leap years and 59 non-leap years. So, the total number of odd days up to 31st Dec.
- 1978 is 19 x 2 + 59 = 97. On dividing 97 by 7 we get 6 as the remainder, which is the total number of odd days in these years.
- So, till 31st Dec. 1978, we have 1 + 6 = 7 odd days, which forms one complete week.
- Now, in 1979, we have 3 odd days in January, and 2 odd days in the month of February (up to 9th Feb). So, the total odd days are 3 + 2 = 5.
- Hence, 9th February 1979 was a Friday.
Example 2: If May 10, 1997, was a Monday, what will be the day on Oct 10, 2001?
- In this question, the reference point is May 10, 1997, and you have to find the number of odd days from May 10, 1997, up to Oct 10, 2001.
- Now, from May 11, 1997 - May 10, 1998 = 1 odd day
May 11, 1998 - May 10, 1999 = 1 odd day
May 11, 1999 - May 10, 2000 = 2 odd days (2000 was leap year)
May 11, 2000 - May 10, 2001 = 1 odd day- Thus, the total number of odd days up to May 10, 2001 = 5.
- Now, the remaining 21 days of May will give 0 odd days. In June, we have 2 odd days; in July, 3 odd days; in August, 3 odd days; in September, 2 odd days and up to 10th October, we have 3 odd days.
- Hence, total number of odd days = 18 i.e. 4 odd days. Since, May 10, 1997 was a Monday, then 4 days after Monday will be Friday. So, Oct 10, 2001, would be a Friday.
Example 3: If 11th April 1911 was a Tuesday, what would be the day on 17th September 1915?
- Firstly in terms of years, the year 1911 to 1912 would give us 2 odd days and 1913, 1914, 1915 would give 1, 1 and 1 odd day respectively.
- Now shift the focus on months. If you move one month ahead i.e. from 11th April to 11th May, the month ending in between is April, which gives you 2 days. Now after that, the month of May, June, July, and August gives you 3, 2, 3, and 3 odd days respectively.
- With this, you reach on 11th September 1915. After this, there are 6 more September days (from 11th to 17th September).
- The total number of odd days is 2 + 1 + 1 + 1 + 2 + 3 + 2 + 3 + 3 + 6 = 24.
- Subtracting 21 (3 full weeks) from this the odd number of days left is 3. Adding three days to the day given i.e. Tuesday, the answer becomes Friday.
Example 4: If 15 March 1816 was Friday, what day of the week would 15th April 1916 be?
- We are given that 15th March 1816 was a Friday.
- Now we know that 100 years have 5 odd days. So till 15th March 1916, we will be having 5 odd days. So if we move from 15th March 1816 to 15th March 1916, we will encounter 5 odd days.
- Now from 15th March 1916 to 15th April 1916 there would be 3 odd days.
- So total number of odd days = 5+3 =8
8 mod 7 = 1
So, 15th April 1916 would be Friday + 1= Saturday
Example 5: The leap year 1895 is having the same calendar as that of the year X. Which of the following is a possible value of X.
- 1895 is not a leap year.
- So, it will have 1 odd day.
- Since, 1896 is a leap year, it will add 2 odd days.
- Similarly, 1987, 1898, 1899, 1900 will add 1,1,1,1 odd days.Now the total number of odd days add up to 7.
- So, the next year 1901 will have the same calendar as 1895.
Important Formulae: CAT Calendars
- Odd Days: If the question is asking to find the day of the week on a given date, the students need to use the concept of odd days.
- The number of days more than the completed week are called odd days.
- Leap Year: Every year which is divisible by 4 is a leap year and every fourth century is a leap year and no other century is a leap year.
For instance, Each of the years 1948, 2004, 1676 - each of them is a leap year.
400, 800, 1200, 1600, 2000 - each of them is a leap year.
2001, 2002, 2003, 2005, 1800, 2100 - none among them is a leap year. - Ordinary year: The year which is not a year is called an ordinary year. An ordinary year has a total of 365 days
- Counting of odd days: 1 year has a total of 52 weeks and 1 day. Hence, 1 ordinary year has 1 odd day
- 1 leap year has 52 weeks and 2 days. Hence, 1 leap year has 2 odd days.
- 100 years has 76 ordinary years and 24 leap years
= (76 x 1 + 24 x 2) odd days = 124 odd days. = (17 weeks + days) 5 odd days. Hence, the number of odd days in 100 years is five - The number of odd days in 200 years will be (5 X 2)= 3 odd days
- The number of odd days in 300 years will be (5 X 3)= 1 odd day
- The number of odd days in 400 years will be (5 X 4+1)= 0 odd day
|
88 videos|119 docs|91 tests
|
FAQs on Concept of Calendars - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is the importance of calendar-based questions in exams? |  |
| 2. What is the basic structure of a calendar? |  |
| 3. What are odd days in a calendar? |  |
| 4. What is a leap year? |  |
| 5. How can calendar calculations be solved? |  |
|
88 videos|119 docs|91 tests
|





















