Modulo Arithmetic | Applied Mathematics for Class 12 - Commerce PDF Download

An Introduction to Modular Math

When we divide two integers we will have an equation that looks like the following:
A/B = Q remainder R

• A is the dividend
• B is the divisor
• Q is the quotient
• R is the remainder

Sometimes, we are only interested in what the remainder is when we divide A by B.
For these cases there is an operator called the modulo operator (abbreviated as mod).
Using the same A, B, Q, and R as above, we would have: A mod B = R
We would say this as A modulo B is equal to R. Where B is referred to as the modulus.
For example:
13/5 = 2 remainder 3
13 mod 5 = 3

Visualize modulus with clocks

Observe what happens when we increment numbers by one and then divide them by 3.
0/3 = 0 remainder 0
1/3 = 0 remainder 1
2/3 = 0 remainder 2
3/3 = 1 remainder 0
4/3 = 1 remainder 1
5/3 = 1 remainder 2
6/3 = 2 remainder 0
The remainders start at 0 and increases by 1 each time, until the number reaches one less than the number we are dividing by. After that, the sequence repeats.
By noticing this, we can visualize the modulo operator by using circles.
We write 0 at the top of a circle and continuing clockwise writing integers 1, 2, ... up to one less than the modulus.
For example, a clock with the 12 replaced by a 0 would be the circle for a modulus of 12.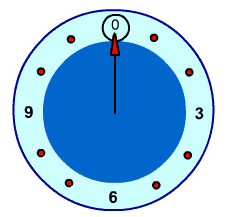
To find the result of A mod B follow these steps:

• Construct this clock for size B
• Start at 0 and move around the clock A steps
• Wherever we land is our solution.

(If the number is positive we step clockwise, if it's negative we step counter-clockwise.)

Examples

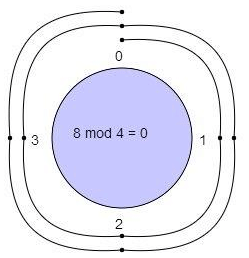
8 mod 4 = ?

With a modulus of 4 we make a clock with numbers 0, 1, 2, 3.
We start at 0 and go through 8 numbers in a clockwise sequence 1, 2, 3, 0, 1, 2, 3, 0.

We ended up at 0 so 8 mod 4 = 0.

7 mod 2 = ?

With a modulus of 2 we make a clock with numbers 0, 1.
We start at 0 and go through 7 numbers in a clockwise sequence 1, 0, 1, 0, 1, 0, 1.

We ended up at 1 so 7 mod 2 = 1.

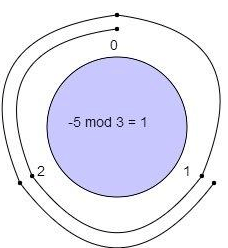
−5 mod 3 = ?

With a modulus of 3 we make a clock with numbers 0, 1, 2.
We start at 0 and go through 5 numbers in counter-clockwise sequence (5 is negative) 2, 1, 0, 2, 1.
We ended up at 1 so -5 mod 3 = 1