Modulus & Conjugate of a Complex Number | Mathematics (Maths) Class 11 - Commerce PDF Download
Conjugate of A Complex Number
Complex numbers are represented in a binomial form as (a + ib). It almost invites you to play with that ‘+’ sign. What happens if we change it to a negative sign? Let z = a + ib be a complex number. We define another complex number 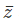 such that
such that 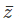 = a – ib. We call
= a – ib. We call 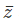 or the complex number obtained by changing the sign of the imaginary part (positive to negative or vice versa), as the conjugate of z. Let us now find the product z
or the complex number obtained by changing the sign of the imaginary part (positive to negative or vice versa), as the conjugate of z. Let us now find the product z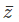 = (a + ib)×(a – ib)
= (a + ib)×(a – ib)
Hence, z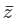 = {a2 -i(ab) + i(ab) + b2 } = (a2 + b2 ) …(1)
= {a2 -i(ab) + i(ab) + b2 } = (a2 + b2 ) …(1)
If a and b are large numbers, the sum in (1) will be greater. So one can use this equation to measure the value of a complex number.
The complex conjugates of complex numbers are used in “ladder operators” to study the excitation of electrons!
Modulus of A Complex Number
There is a way to get a feel for how big the numbers we are dealing with are. We take the complex conjugate and multiply it by the complex number as done in (1). Hence, we define the product z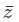 as the square of the Absolute value or modulus of a complex number. Therefore, we can write z
as the square of the Absolute value or modulus of a complex number. Therefore, we can write z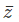 = |z|2
= |z|2
This is done because as we just discussed, z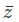 gives a way to measure the Absolute value or magnitude of our complex number. The actual reason for this definition will get clear once you learn about the Argand Plane.
gives a way to measure the Absolute value or magnitude of our complex number. The actual reason for this definition will get clear once you learn about the Argand Plane.
Therefore, |z|2 = (a2 + b2) [Using (1)]
Hence, |z| = 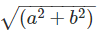 …(2)
…(2)
The above equation represents the modulus or the absolute value of our complex number z.
Important Identities
If |z|2 = 1 = |z|, i.e. z is a complex number of unit modulus, then from (1), we have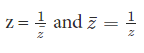
Also If z1 and z2 is any complex number, we have the following identities:
• |z1 z2| = |z1| |z2|
• Modulus (z1 / z2)= Modulus of z1 /Modulus of z2
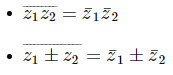
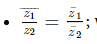 with the accord that z2 ≠ 0
with the accord that z2 ≠ 0
Solved Examples
Example 1: If z = 2 – i, find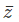 ?
?
Solution: All we need to do is to change the sign of the imaginary term. Therefore, we denote it as follows:
z = 2 – i or (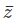 )=
)= 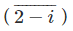
Now ¯ or ‘bar’ or ‘dagger’ becomes an operation that transforms the imaginary part of a complex number in sign. In other words, we can write: 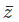 = 2 + i. Note that there is no change in the sign of 2.
= 2 + i. Note that there is no change in the sign of 2.
Example 2: If z = a+ib, show that |z|2 = z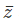 .
.
Solution: We know that 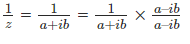
Therefore, we have 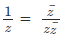 [using the definition of conjugate]
[using the definition of conjugate]
Hence, 1z = 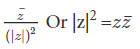
Example 3: The maximum value of ∣z∣ when z satisfies the condition ∣z+ 2/z ∣ = 2 is:
A) 1
B) √3 + 1
C) √3 – 1
D) -1
Solution: B)
We have the condition that modulus ( z + 2/z ) = 2. Therefore, can we not treat this as an equation in one variable? We can but the equation would be second order in z and we won’t be able to get a relation for |z| alone. So we do the following:
|z| can be written as = |z + [2/z] – [2/z]| ≤ |z + [2/z]| ≤ |z + [2/z]| + 2/|z|
Therefore, |z| ≤ 2 + 2/|z| Or |z| ≤ (2|z| + 2)/|z|
Hence, |z|2 ≤ 2|z| + 2 Or |z|2 – 2|z| ≤ 2
To get the value of |z|, let’s convert the LHS of the above equation into a perfect square. After adding 1 on both the side, we have |z|2 – 2|z|(1) + (1)2 ≤ 2 + (1)2
(|z| – 1)2 ≤ 3
Therefore, – √3 ≤ (|z| – 1) ≤ √3
Hence, the maximum value of |z| will be √3 + 1
|
80 videos|315 docs|99 tests
|
FAQs on Modulus & Conjugate of a Complex Number - Mathematics (Maths) Class 11 - Commerce
| 1. What is the modulus of a complex number? |  |
| 2. What is the conjugate of a complex number? |  |
| 3. How do you find the modulus of a complex number in polar form? |  |
| 4. What is the relationship between the modulus and conjugate of a complex number? |  |
| 5. How do you find the argument of a complex number in rectangular form? |  |
















