Momentum & Energy | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| Newton’s Law of Viscosity |

|
| Variation of Viscosity with Temperature |

|
| Types of Fluids |

|
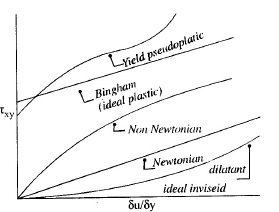
| Rheological Classification of Fluids |

|
| Thermodynamic Properties |

|
| Solved Numericals |

|
Newton’s Law of Viscosity
It states that the shear stress (τ) on a fluid element layer is directly proportional to the rate of shear strain. Mathematically, Fluids which obey the above relation are known as Newtonain fluids and the fluids which do not obey the above relation are called Non−Newtonain fluids.
Fluids which obey the above relation are known as Newtonain fluids and the fluids which do not obey the above relation are called Non−Newtonain fluids.
Variation of Viscosity with Temperature
Viscosity behaves differently with temperature depending on whether the substance is a liquid or a gas.- Viscosity of Liquids: In liquids, viscosity tends to decrease as temperature increases. This phenomenon occurs because liquids have closely packed molecules with significant cohesive forces between them. At lower temperatures, these cohesive forces are stronger, hindering the flow of molecules past each other and thus increasing viscosity. As temperature rises, the cohesive forces weaken, allowing molecules to move more freely and reducing viscosity.
- Viscosity of Gases: On the other hand, the viscosity of gases generally increases with temperature. This is because gases have weaker cohesive forces compared to liquids, and their viscosity is primarily influenced by molecular momentum transfer. As temperature rises, the kinetic energy of gas molecules increases, leading to more frequent collisions and interactions between molecules. This increased molecular activity results in greater internal friction and resistance to flow, thereby increasing viscosity.
The relation between viscosity and temperature for liquids and gases is :
For Liquids, 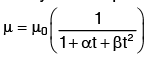
where μ = Viscosity of liquid at t°C, in poise
μ0 = Viscosity of liquid at 0°C, in poise
α, β are constants for the liquid
For water, μ0 = 1.79 × 10−3 poise, α = 0.03368 and β = 0.000221
For gases, μ = μ0 + αt − βt2
where for air; μ0 = 0.000017, α = 0.000000056, β = 0.1189 × 10−9
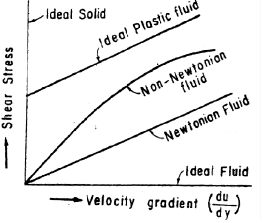
Types of Fluids
Ideal Fluid: An ideal fluid is an imaginary fluid that is incompressible (density remains constant) and has no viscosity (internal friction). It serves as a theoretical model and does not exist in reality.
Real Fluid: A real fluid is any fluid that possesses viscosity, which is the resistance to flow. In practical terms, all fluids encountered in everyday life, such as water, oil, and air, are real fluids.
Newtonian Fluid: A Newtonian fluid is a type of real fluid that obeys Newton's law of viscosity. According to this law, the shear stress between adjacent fluid layers is directly proportional to the velocity gradient (rate of change of velocity with respect to distance) in the direction perpendicular to the layers.
Non-Newtonian Fluid: A non-Newtonian fluid is a real fluid that does not obey Newton's law of viscosity under all conditions. These fluids may exhibit shear-thinning (viscosity decreases with increasing shear rate), shear-thickening (viscosity increases with increasing shear rate), or other types of complex behaviors depending on the applied stress or shear rate.
Ideal Plastic Fluid: An ideal plastic fluid is a type of non-Newtonian fluid where the shear stress is greater than a certain yield value (yield stress), and the shear stress is directly proportional to the rate of shear strain (velocity gradient) once the yield stress is exceeded. This means that the fluid behaves like a solid below the yield stress and flows like a fluid above it.
 Types of fluids
Types of fluids
Rheological Classification of Fluids
There are two major types of Non−Newtonian fluids : Viscoelastic and Purely viscous fluids. Viscoelastic fluids are characteristized by equation Where E is modulus of elasticity and α is a constant of fluid. A mixture of solid and liquid flowing through a pipe is an example of viscoelastic fluid (slurry). Purely Viscous fluids are characterized by the equation:
Where E is modulus of elasticity and α is a constant of fluid. A mixture of solid and liquid flowing through a pipe is an example of viscoelastic fluid (slurry). Purely Viscous fluids are characterized by the equation: 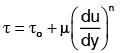 (i) If τo = 0, n < 1 it is pseudoplastic fluid (e.g. fine particle suspension, milk, blood)
(i) If τo = 0, n < 1 it is pseudoplastic fluid (e.g. fine particle suspension, milk, blood)(ii) If τo = 0, n > 1 it is dilatant fluid (e.g. ultrafine irregular particle suspension, concentrated solution of sugar in water)
(iii) If τo = τo, n = 1 it is Bingham fluid (e.g. Hydrocarbon grease, clay suspended in water)
(iv) If τo = τo, n > 1 it is yield pseudoplastic fluid (e.g. carboxypolymethylene)
Above four cases are time independent. There are two time dependent purely viscous fluids governed by the following equations:
(i) Rheopectic fluids : 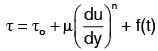 f(t) increases with time.
f(t) increases with time.
(ii) Thixotropic fluids : 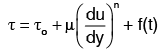 f(t) decreases with time.
f(t) decreases with time.
Thermodynamic Properties
Gases are compressible fluids and hence thermodynamic properties play an important role. With the change of pressure and temperature, the gases undergo large variation in density. The relationship between pressure (absolute), specific volume and absolute temperature of a gas is given by equation of state as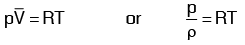 where p = Absolute pressure of a gas in N/m2
where p = Absolute pressure of a gas in N/m2V = specific volume = 1 / ρ
R = Gas constant = 287 J/kg−K
T = Absolute temperature in °K
ρ = Density of gas
1. Isothermal Process : If the change in density occurs at constant temperature, then the process is called isothermal and relationship between pressure and density is given by

2. Adiabatic P rocess : If the change in density occurs with no heat exchange to and from the gas, the process is called adiabatic. And if no heat generated within the gas due to friction, the relationship between pressure and density is given by

where k = Ratio of specific heat of a gas at constant pressure and constant volume = 1.4 for air
Another form of equation of state ; PV = nRT
where V = volume of gas
n = number of moles in a volume of gas
R = universal gas constant = 8.314 × 103 J/kg−mole K.
Solved Numericals
Q1: The 'momentum correction factor' for a laminar flow through a circular pipe is:
Ans: Momentum correction factor - The momentum correction factor is defined as the ratio of momentum of the flow per second based on actual velocity to the momentum of the flow per second based on average velocity across a section.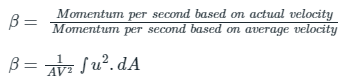 For laminar flow through a circular pipe, β = 4/3 = 1.33
For laminar flow through a circular pipe, β = 4/3 = 1.33
Q2: The velocity distribution over one half of a cross section is uniform and is zero over the remaining half. The momentum correction factor for this cross section is
Ans: The momentum correction factor is defined as the ratio of momentum of the flow per second based on actual velocity to the momentum of the flow per second based on average velocity across a section.
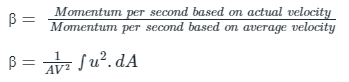 u = actual velocity, V = average velocity
u = actual velocity, V = average velocity
Calculation:
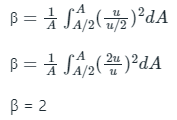
Q3: The velocity distribution over one half of a cross section is uniform and is zero over the remaining half. The momentum correction factor for this cross section is
Ans: The momentum correction factor is defined as the ratio of momentum of the flow per second based on actual velocity to the momentum of the flow per second based on average velocity across a section.
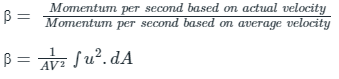
u = actual velocity, V = average velocity
Calculation:
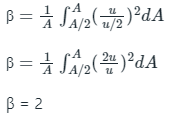
|
56 videos|104 docs|75 tests
|
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|